Curvature

1. Principal curvature

• 主曲率
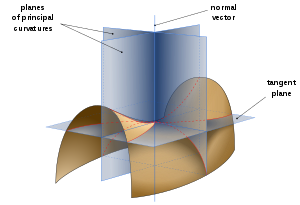
• 维基百科定义: 在曲面上取一点E，曲面在E点的法线为z轴，过z轴可以有无限多个剖切平面，每个剖切平面与曲面相交，其交线为一条平面曲线，每条平面曲线在E点有一个曲率半径。不同的剖切平面上的平面曲线在E点的曲率半径一般是不相等的。这些曲率半径中，有一个最大和最小的曲率半径，称之为主曲率半径，记作 k1 与 k2，这两个曲率半径所在的方向，数学上可以证明是相互垂直的。
• 曲线的曲率由定义是密切圆半径的倒数。当曲线转向与平面给定法向量相同方向时，曲率取正值，否则取负值。
  

2. Gaussian Curvature

• 高斯曲率

• 两个主曲率的乘积 k1k2 是高斯曲率 K_G
  

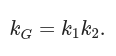
• 离散高斯曲率定义为

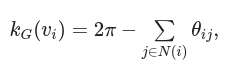
• 高斯曲率含义:

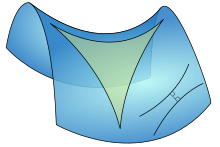
• 负曲率曲面上的三角形三角之和小于平面三角形的三角之和。

• 正曲率曲面上的三角形三角之和小于平面三角形的三角之和。

• C++ code

  void gaussian_curvature(const Eigen::MatrixXd & V,
  const Eigen::MatrixXi & F,
  Eigen::MatrixXd & K) {
  /// 计算每个conner的角度
  Eigen::MatrixXd A;
  internal_angles(V, F, A);
  K.setConstant(V.rows(), 1, 2*igl::PI);
  /// K_G(x_i) = (2π - ∑θj)
  for(int i=0; i<F.rows(); i++) {
  for(int j=0; j<3; j++) {
  K(F(i, j), 0) -= A(i, j);
  }
  }
  }
  

3. Mean curvature

• 平均曲率

• 主曲率的平均值 (k1+k2)/2 是平均曲率 H

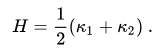
• 对 3 维空间中的曲面，平均曲率与曲面的单位法向量相关：

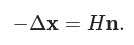
最后

以上就是漂亮往事为你收集整理的Triangle中的曲率CurvatureCurvature的全部内容，希望文章能够帮你解决Triangle中的曲率CurvatureCurvature所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。