三维向量变化为角度_2.2 三维空间位姿描述

书上写的太难了，一天时间简单的了解了一下，不知道会不会影响以后的学习/(ㄒoㄒ)/~

1. 一些知识

• 旋转、平移

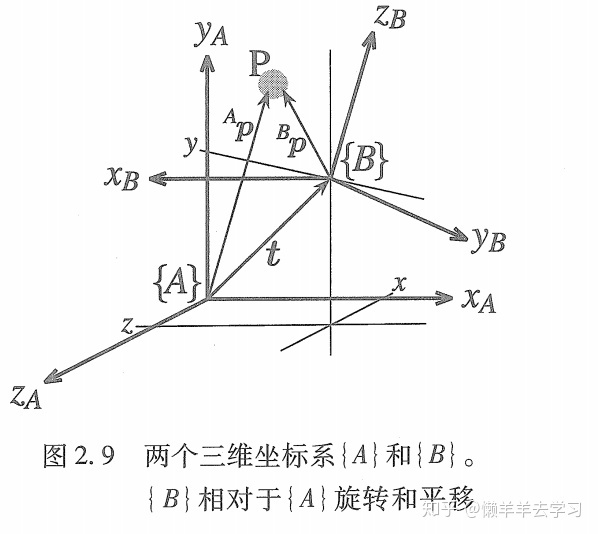
笛卡尔坐标系{A}通过向量t平移，再以某种方式旋转到坐标系{B}，三维的旋转很复杂啊。

• 欧拉旋转定理

任何一个正交坐标系，都可以通过不超过三次相对于坐标轴的旋转，与另一任选直角坐标系方向相同，每连续两次旋转不能绕同一轴绕。

• 右手定则

拇指指向x，四指伸向y，四指弯曲的方向是z。

• 向量旋转方向

手握住向量，拇指指向向量方向，四指的方向就是旋转的正方向。

2. 3D变换矩阵

• 旋转

绕x,y,z轴旋转的正交矩阵为：

• 平移

平移的矩阵为：

• 缩放

缩放的矩阵为：

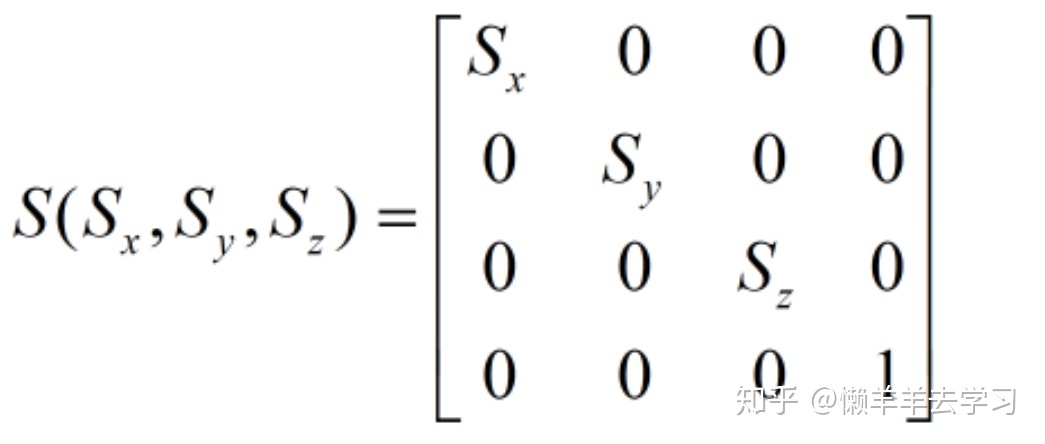
3. 三角度表示法

书上介绍了两种：

• ZYZ序列

在航空、机械动力学，常用ZYZ序列，欧拉角表示为：

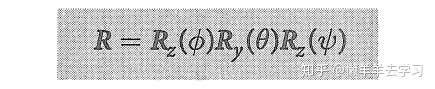
matlab中，给定欧拉角，可生成唯一的旋转矩阵；但旋转矩阵可能会对应多个欧拉角。

且，当

时，

• XYZ序列

船舶、飞机、车辆中，常用XYZ序列，欧拉角表示为：

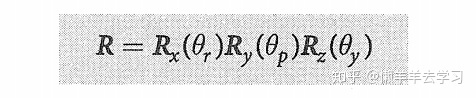
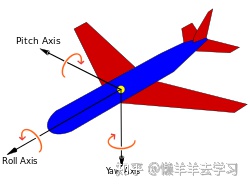
绕x轴旋转 -- roll 横滚角

绕y轴旋转 -- pitch 俯仰角

绕z轴旋转 -- yaw 偏航角

它也有奇异点：

所以，欧拉角不是完全安全的，当x,y,z轴有两个共线时，只有两个自由度，称为万向节死锁。用在车辆上比较好，飞机轮船会有危险。

4.双向量表示法

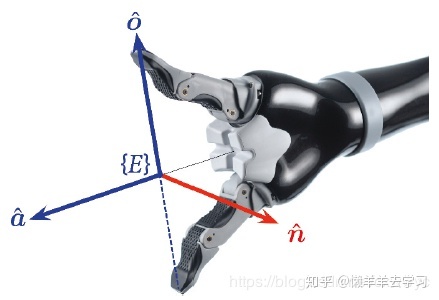
用于关节臂式机器人，一般会在它的末端执行器上固联一个坐标系{

},工具的轴线为坐标系的

轴，称为“接近向量”，记为：

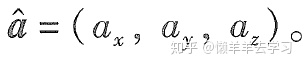
定义“姿态向量”与接近向量正交，穿过两指之间。记为：

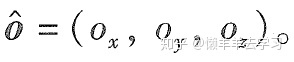
双向量f表示法，大概就是这两个向量了，然后这俩再生成一个与他俩平面垂直的向量

.

5.轴-角法

一个姿态，总是可以找到某一固定轴

，绕着它旋转某一角度

，变为任何我们想要的姿态。

也可使用n罗德里格斯旋转方程，利用角度和向量找到旋转方程：

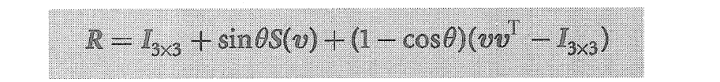
推导见b站。

6.四元数法

太复杂了，大概的定义是，用标量和三个虚轴表示向量，叫四元数。