GAMES101-现代计算机图形学学习笔记（11）点云多边形曲线

GAMES101-现代计算机图形学学习笔记（11）

点云

点云就是一堆点的集合，最简单的点云表示形式就是（x，y，z），x，y，z分别表示每个点在三维空间上的位置。除了坐标以外，每个点的属性还包括颜色（R,G,B）、法线等，如图所示：

非二进制编码的点云文件可以直接用记事本查看，这里举例了一个包含位置、颜色以及法向量的点云文件（.obj文件）。其中每一行 v 包含了顶点（x，y，z）和颜色（r，g，b），vn表示每个点对应的法向量。

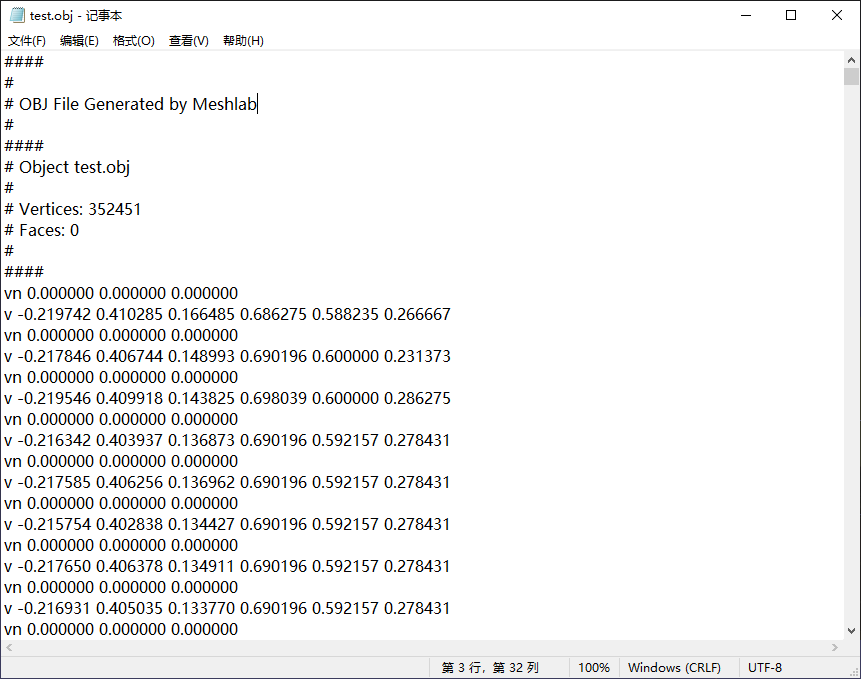
多边形

相比点云，多边形多了一些点与点之间的连接关系。对于一个三角形面片组成的模型来说，也可以用 .obj 文件存储这个模型，同时它也包含了更多如：点的连接关系（f）、纹理坐标（vt）等信息：

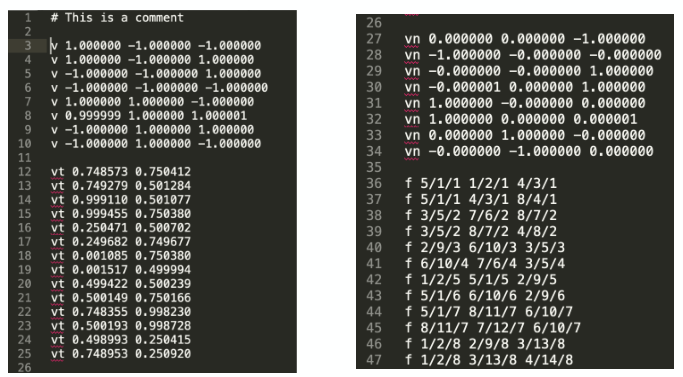
曲线

在计算机图形学应用中，我们经常需要在屏幕上绘制许多不同类型的对象。对象并非都是由平面组成，有些对象可能需要用曲线来进行描绘。为了使得描绘的曲线不受分辨率的影响，研究人员就提出一种曲线–贝塞尔曲线。它是一种显示曲线，由一系列控制点与线段组成，通过它可以得到精确的曲线。

贝塞尔曲线

贝塞尔曲线受限于由一系列控制点，它是通过使用控制点的近似切线生成曲线。已知四个点 $p_1$, $p_2$, $p_3$, $p_4$, 那么贝塞尔曲线就可以表示如下：

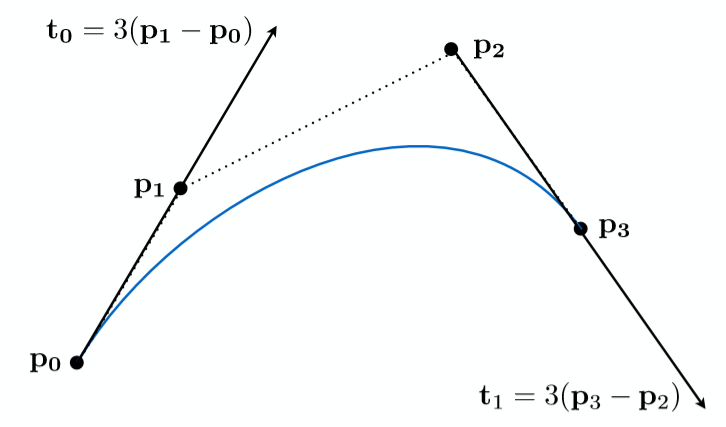
解释

贝塞尔曲线本质就是对线段插值，它是一个类似递归求解的过程。 $Casteljau$ 算法描述了如何求解贝塞尔曲线，下面是该算法对应三个控制点的贝塞尔曲线求解过程：
已知三点 $b_0$ , $b_1$ , $b_2$ ，和插值参数 $t$， 第一次递归插值得到 $b_0➡b_1$ 线段上的 $b_0^1$ 和 b 1 ➡ b 2 b_1 ➡ b_2 b1​➡b

最后

以上就是敏感汽车为你收集整理的GAMES101-现代计算机图形学学习笔记（11）点云多边形曲线的全部内容，希望文章能够帮你解决GAMES101-现代计算机图形学学习笔记（11）点云多边形曲线所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。