计算机图形学笔记1.变换向量 Vectors矩阵变换

向量 Vectors

• Dot product
• Cross product
• Orthonormal bases and coordinate frames

1. Dot product
   

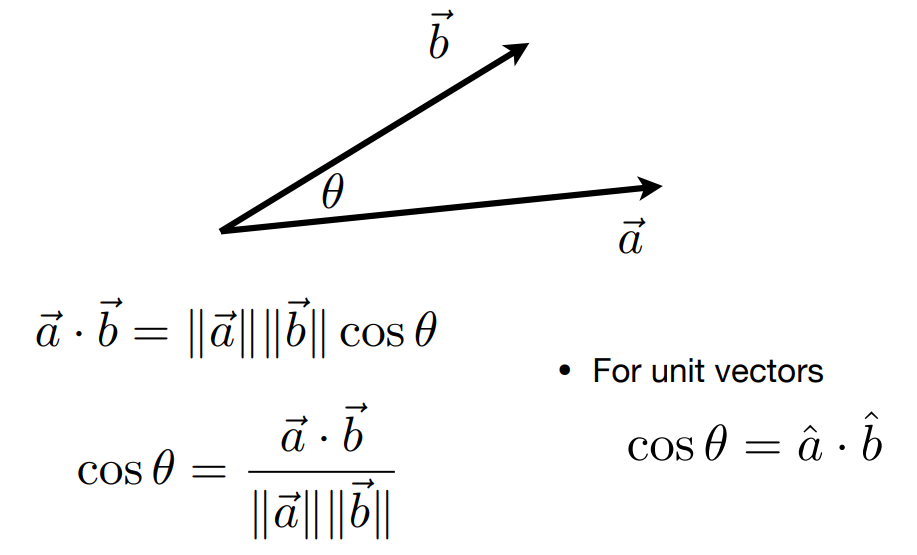
Dot Product in Graphics

• Find angle between two vectors (e.g. cosine of angle between light source and surface)
• Finding projection of one vector on another
  

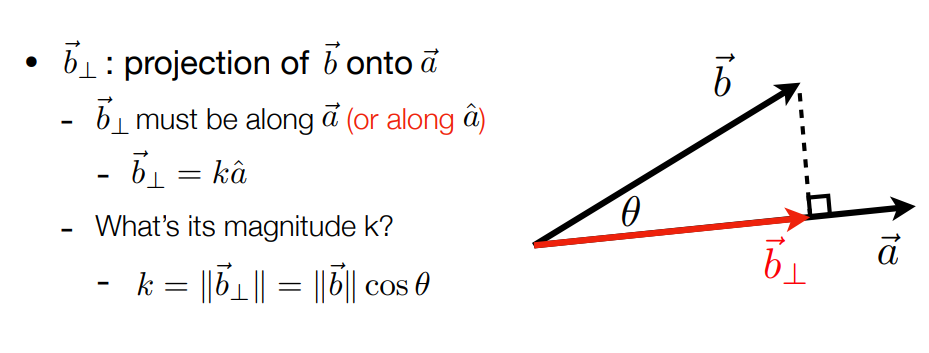
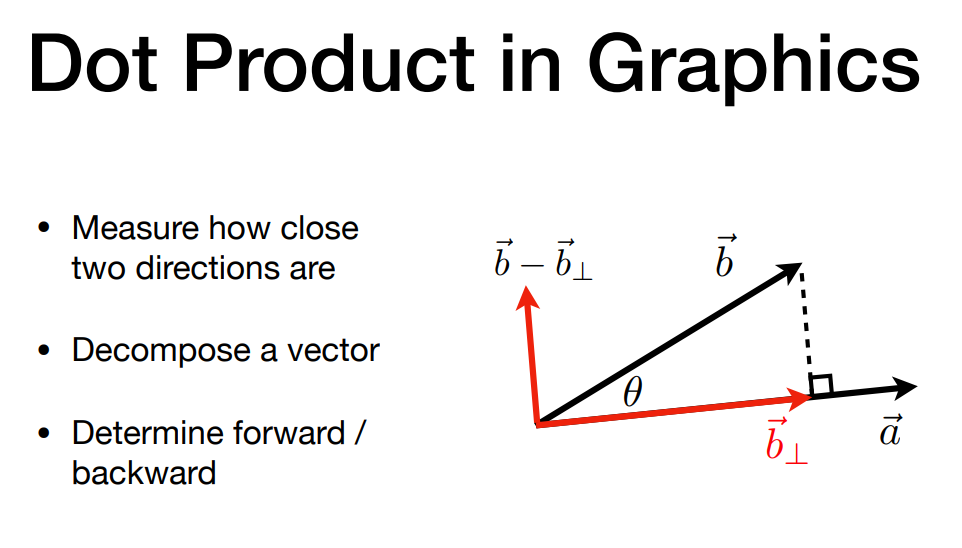
1.向量的点乘可以告诉我们方向性（基本一致、基本相反、基本垂直）
2.两个向量在方向上有多接近

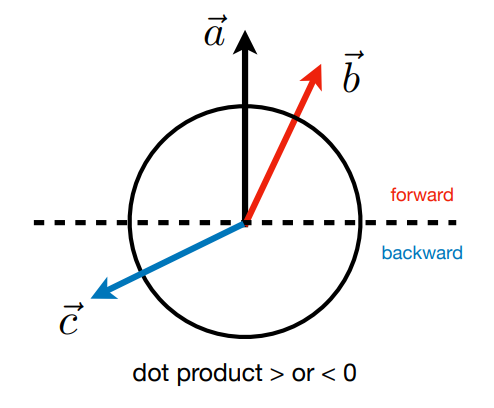
2. Cross product
   右手螺旋定则，拇指方向即两向量叉乘后结果的方向。（也就意味着叉积不满足交换律）
   
   如果在一个坐标系中，向量x叉乘向量y得到向量z，就假设这是右手系。
   
   

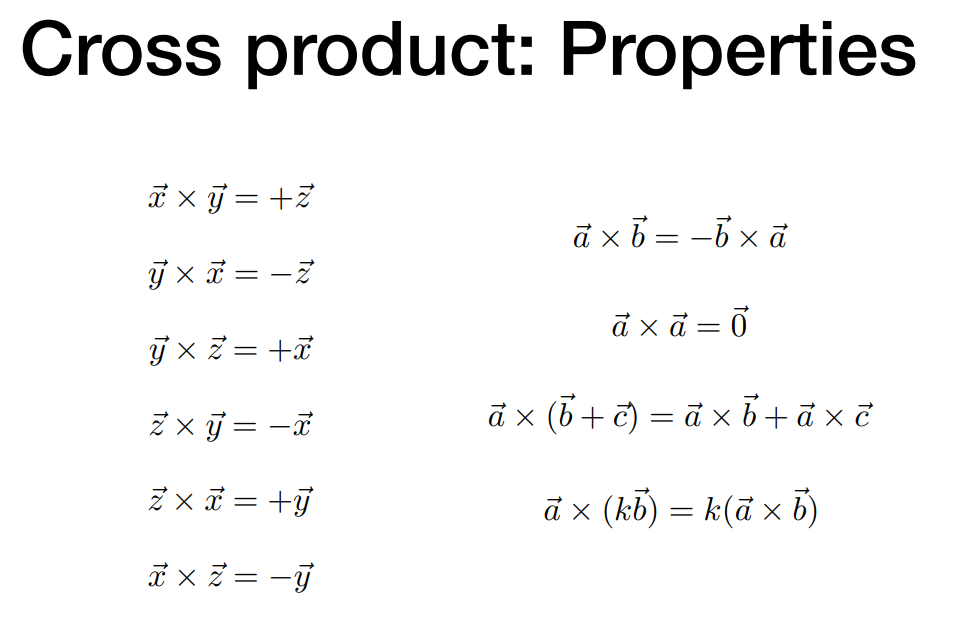
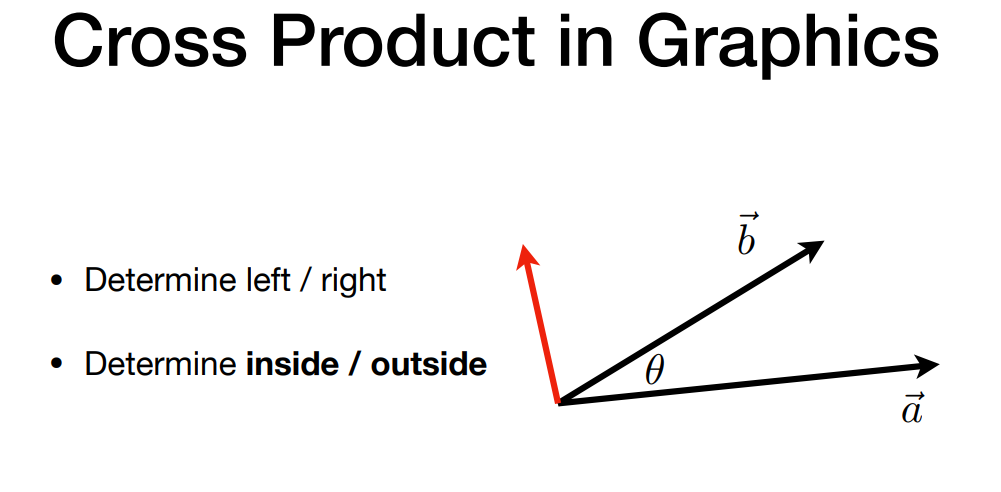
a叉乘b，右手螺旋定则可得到z为正，即b在a左侧；即a在b右侧。

判断p点是否在三角形内部？
AB叉乘AP，得到的结果向外，即p点在AB左侧，同理得到P点在BC左侧，也在CA左侧。
对于任何三角形（不管输入为逆时针或顺时针），P点一直在三条边的左边（或三条边的右边），那么P点就在三角形内部。

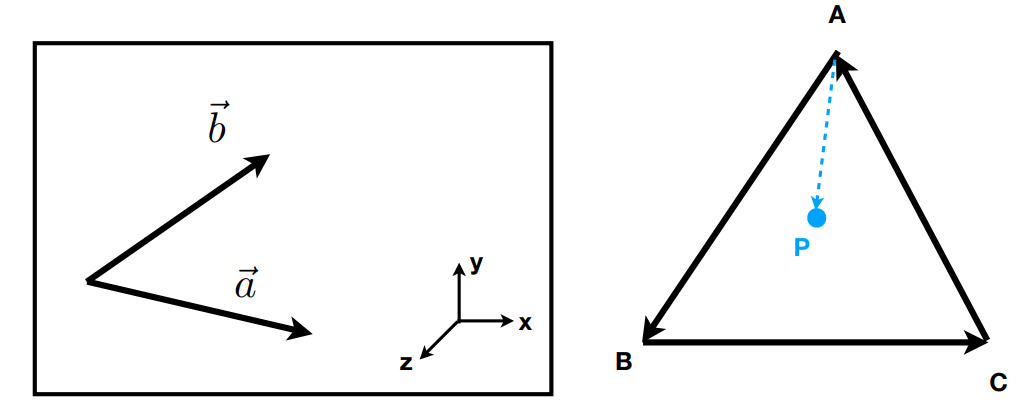
定义一个坐标系：

矩阵

Matrices
Matrix-Matrix Multiplication

• Properties
  Non-commutative(AB and BA are different in general)
  Associative and distributive
  -(AB)C=A(BC)
  -A(B+C) = AB + AC
  -(A+B)C = AC + BC

把一个向量看成列向量，矩阵在左，向量在右

• Transpose of a Matrix
• Identity Matrix and Inverses
• Vector multiplication in Matrix form
  
  

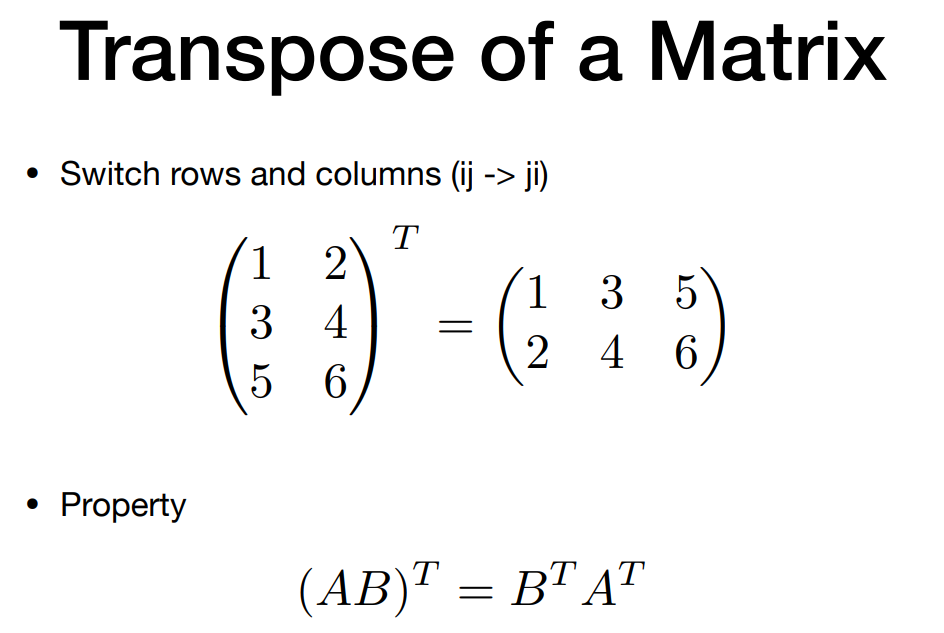
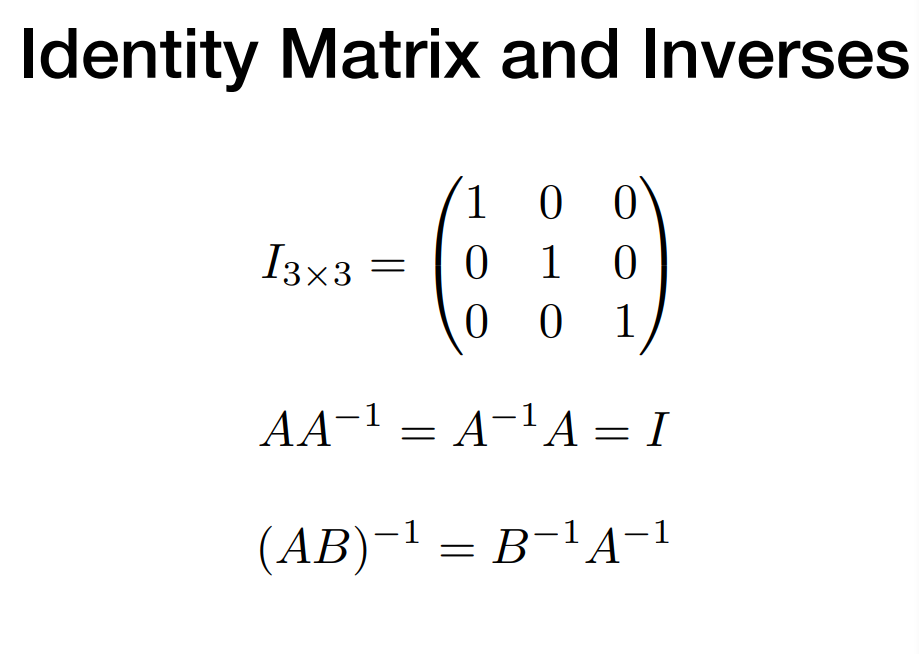
变换

transformation

• Modeling
• Viewing

2D transformations

• Representing transformations using matrices
• Rotation, scale, shear

Homogeneous coordinates

• Why homogeneous coordinates
• Affine transformation

2D:
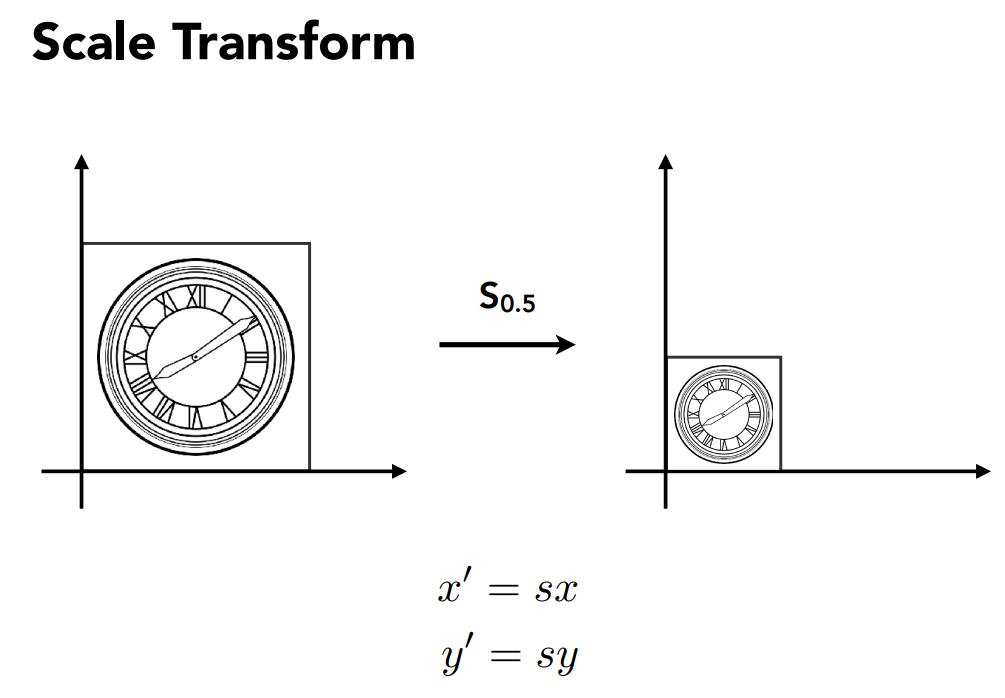
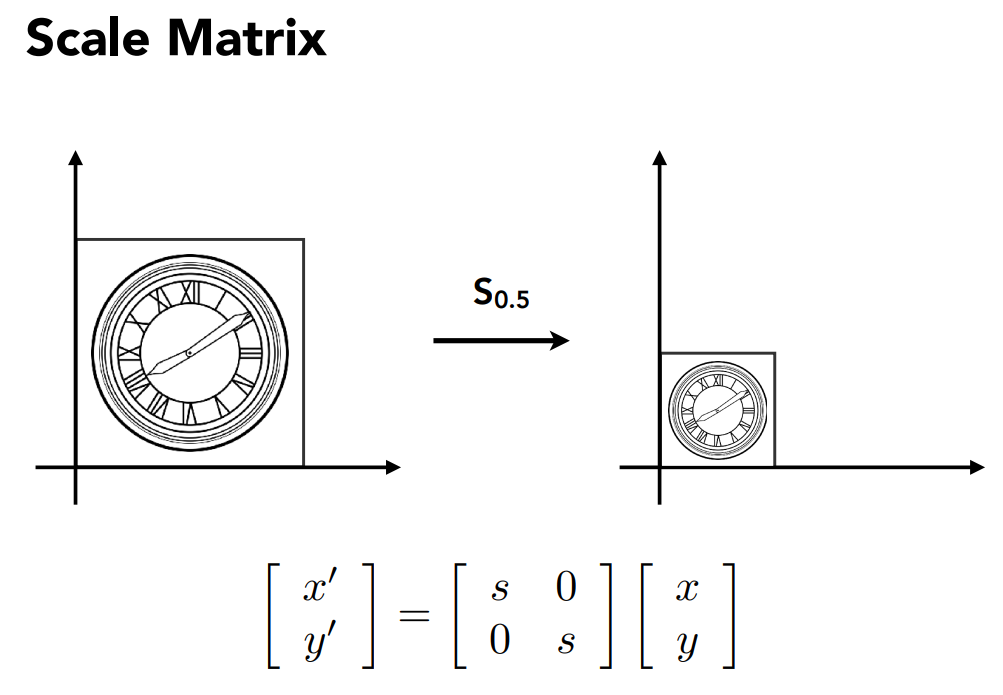
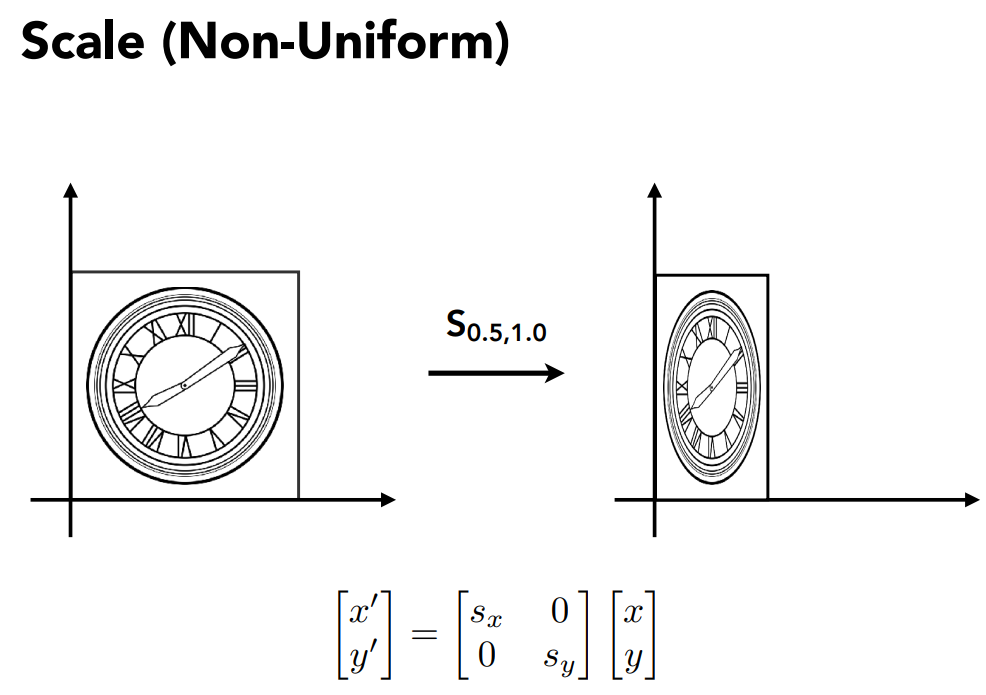
缩放：

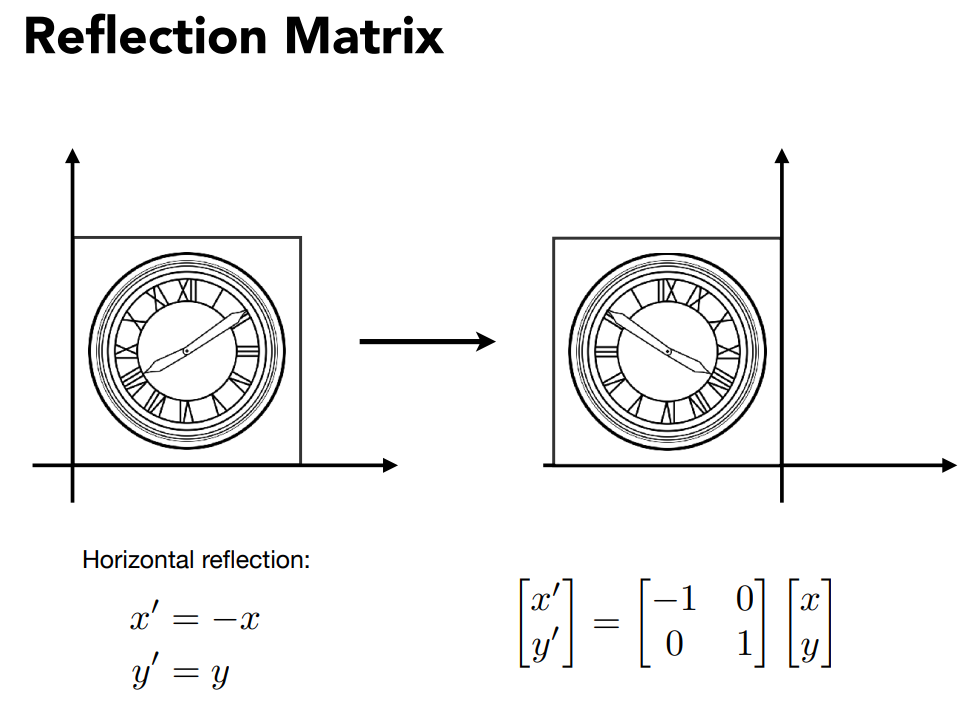
镜像

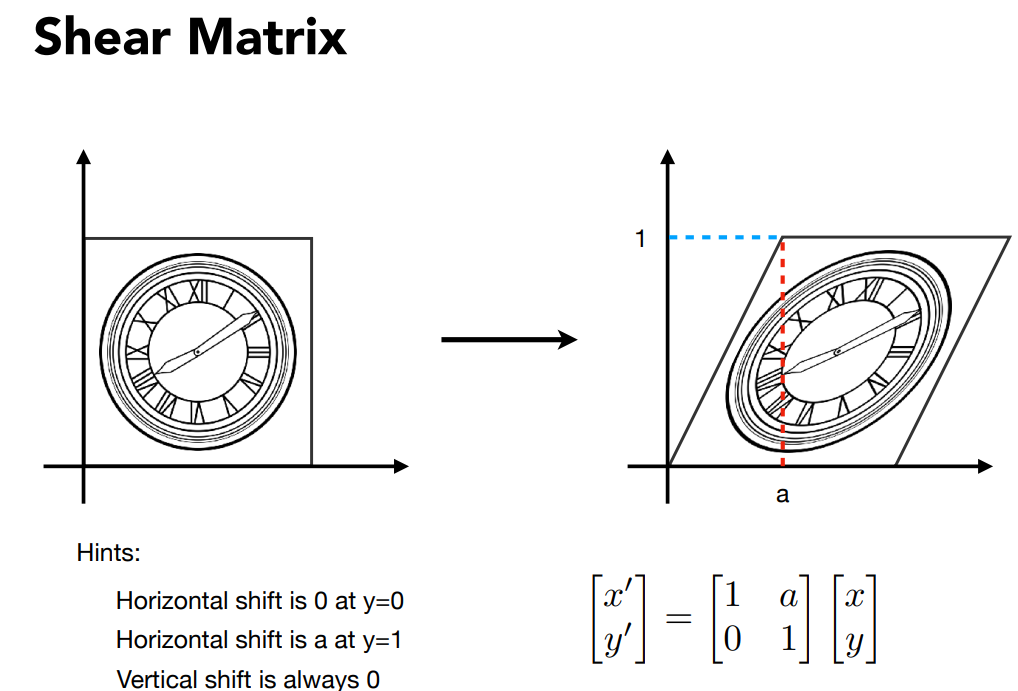
切变：
比如在二分之一a处，水平方向的移动是二分之一乘以a，即a乘以y，可得任何x在水平方向上的移动都是a乘以y

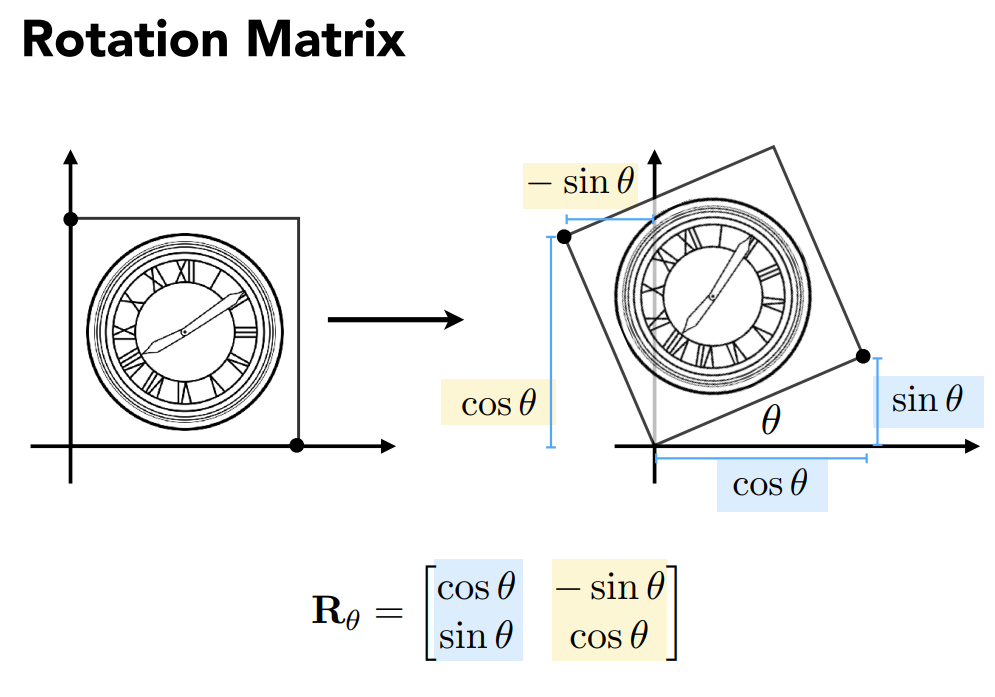
旋转矩阵：
Rotate (about the origin (0, 0), CCW by default)


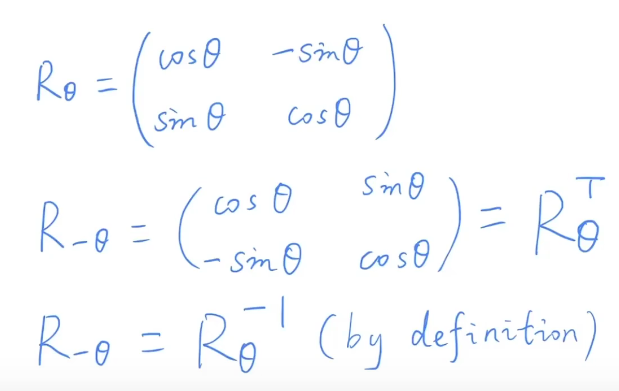
注：一个矩阵的逆等于它的转置，即为正交矩阵

通过两个特殊点推出旋转公式

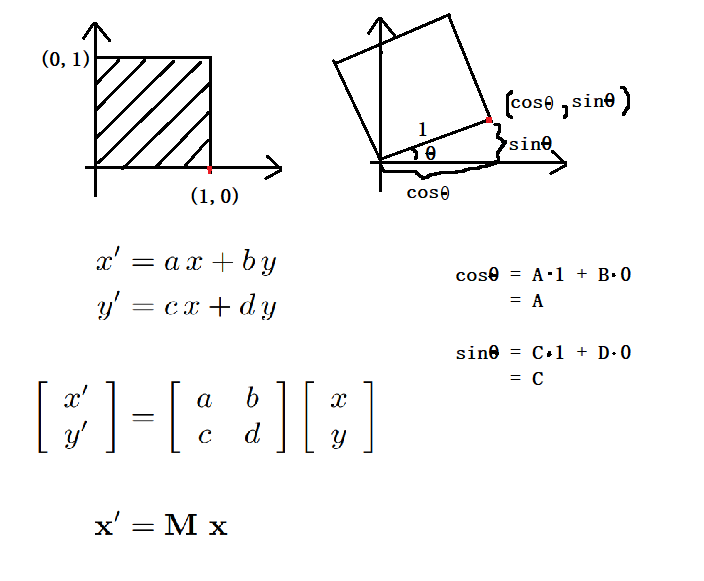
线性变换（写成矩阵形式）

Homogeneous coordinates 齐次坐标
如下平移操作：

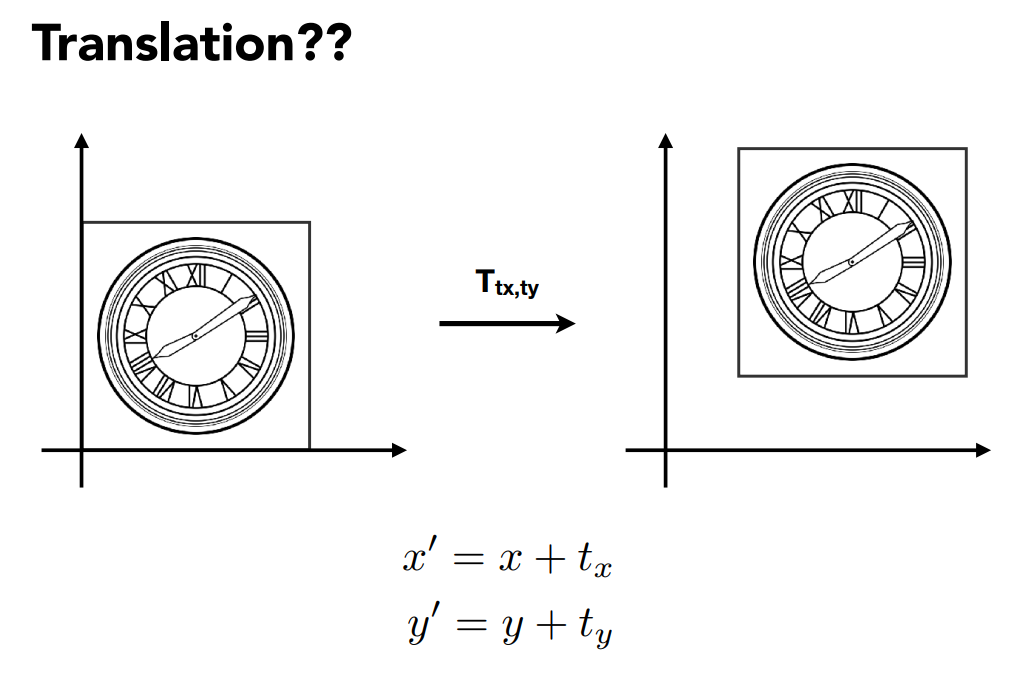
这就不是线性变换了，但我们不想让平移成为一个特例，于是引入了齐次坐标。
向量具有平移不变性，向量的最后一个维度增加一个0，目的是让平移后不变，并且让以下操作正确：
注：在齐次坐标的表示下，两个点相加表示这两个点的中点。

仿射变换可以用齐次坐标表示

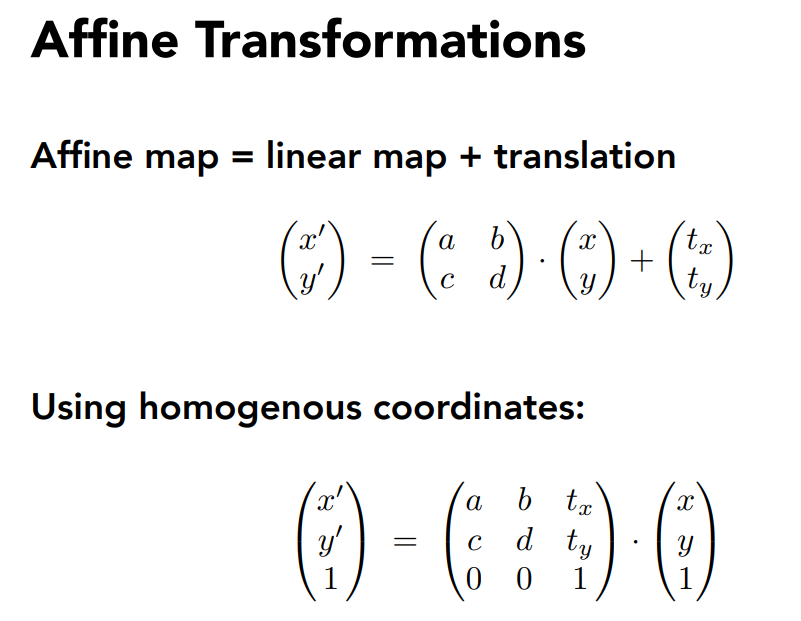
可以用齐次坐标把这些变换写成统一的形式：

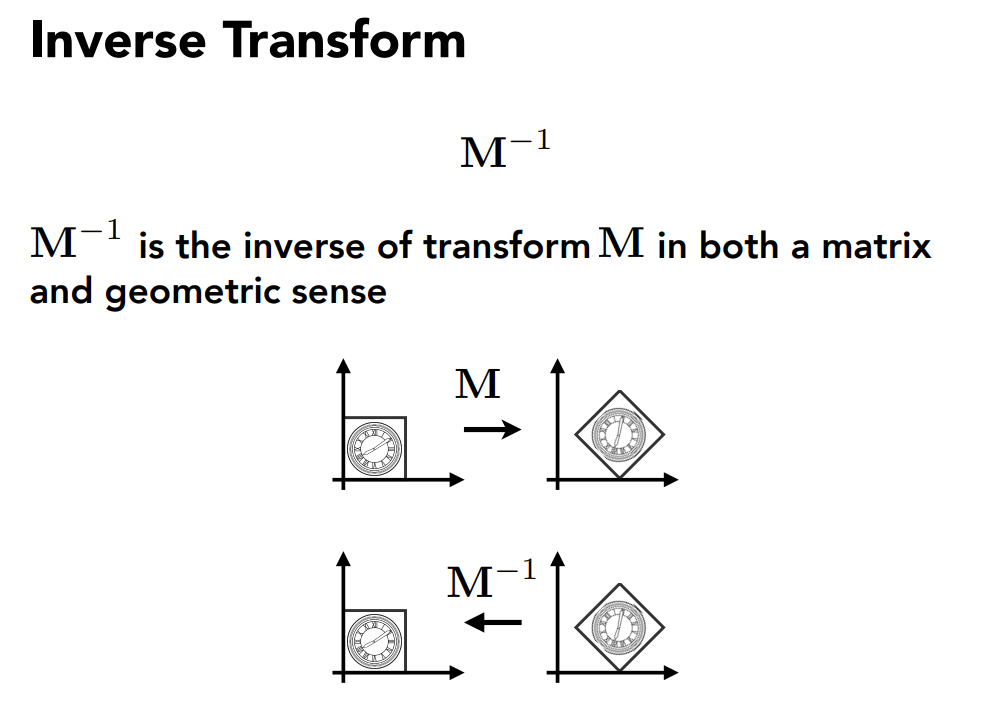
逆变换

Composing Transforms组合变换
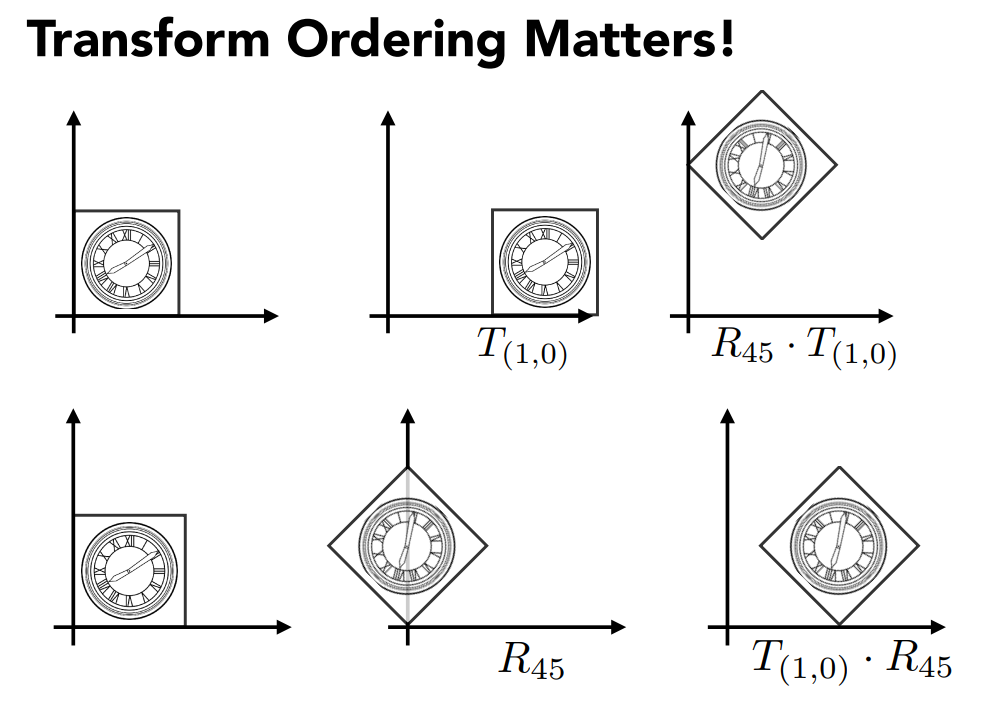从右向左变换


矩阵没有交换律，但有结合律，可以把矩阵相乘成一个矩阵，这个矩阵就表示了很多的变换。

变换的分解：

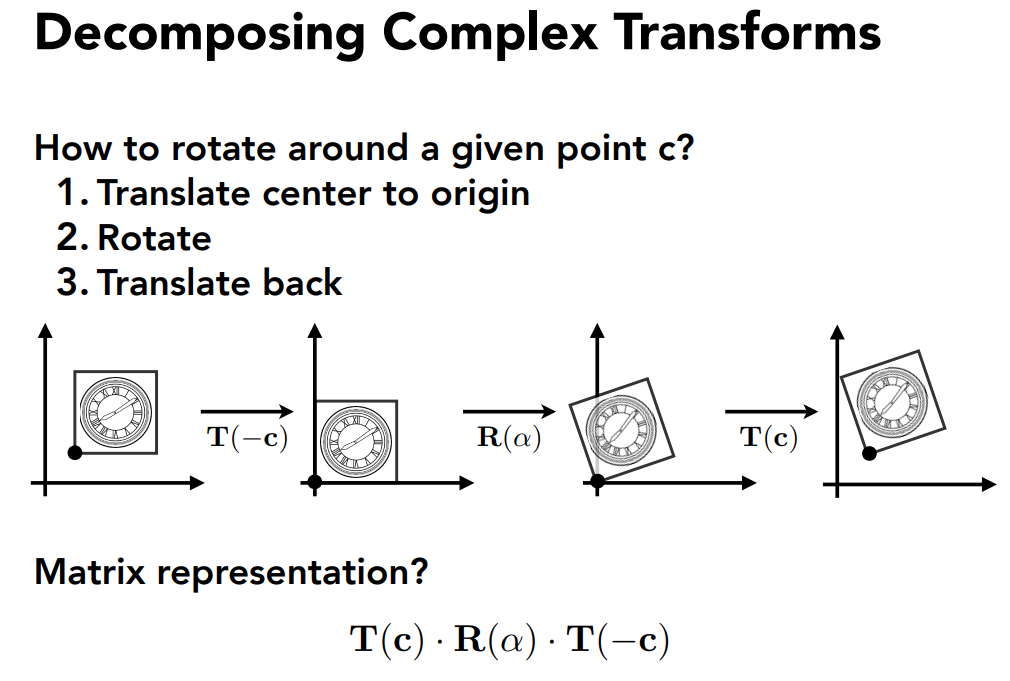
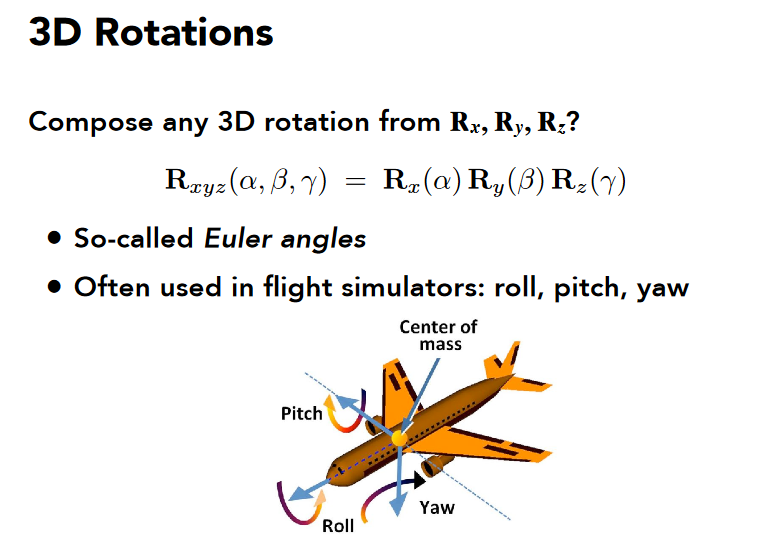
3D Transformations

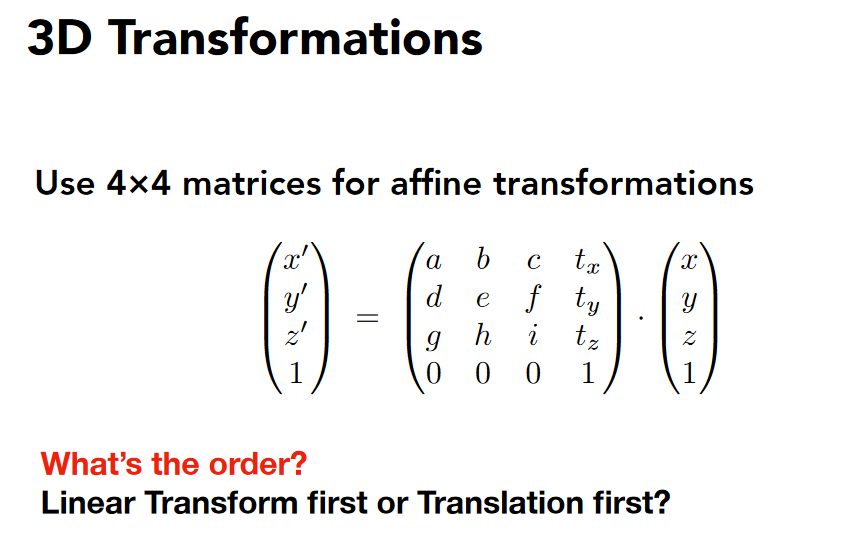先线性变换再平移

变换：

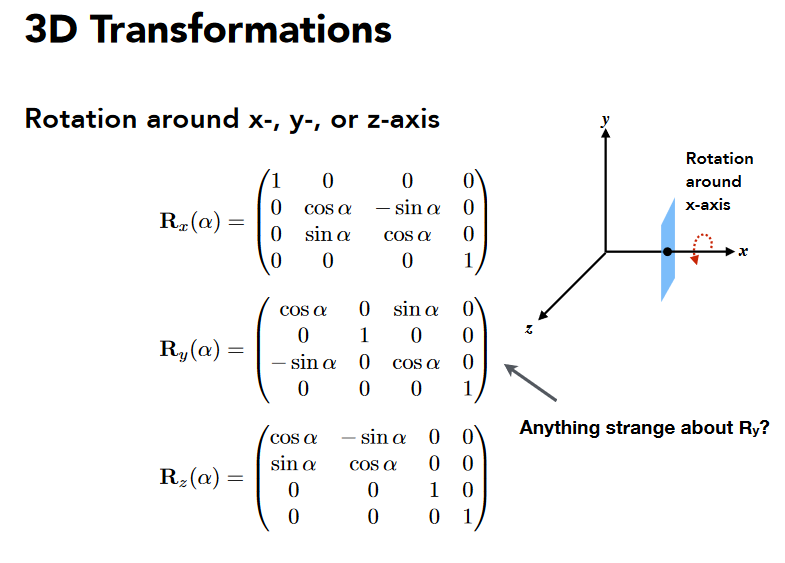
Viewing transformation

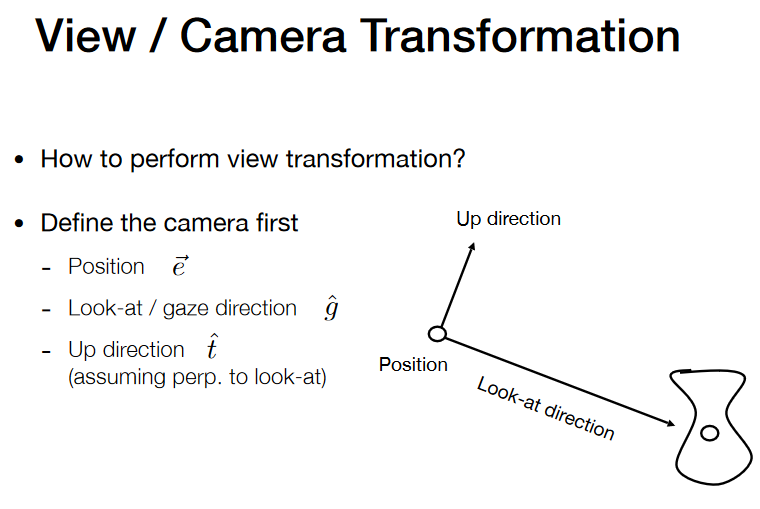
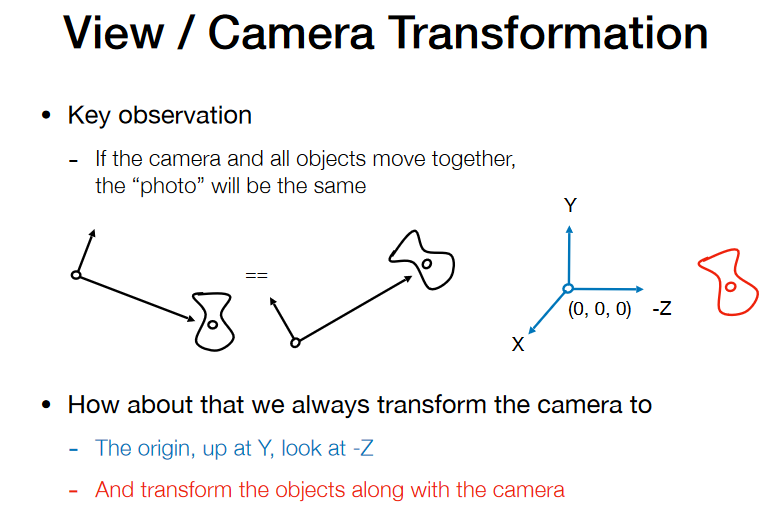
• View / Camera transformation
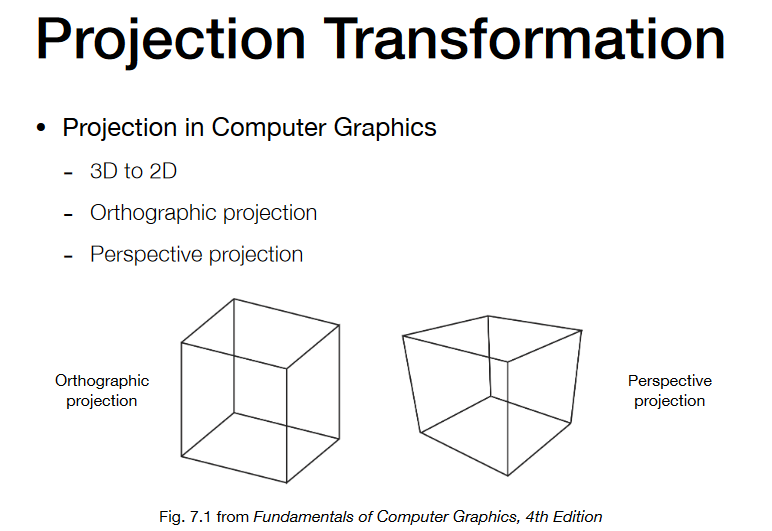
• Projection transformation
  • Orthographic projection
  • Perspective projection

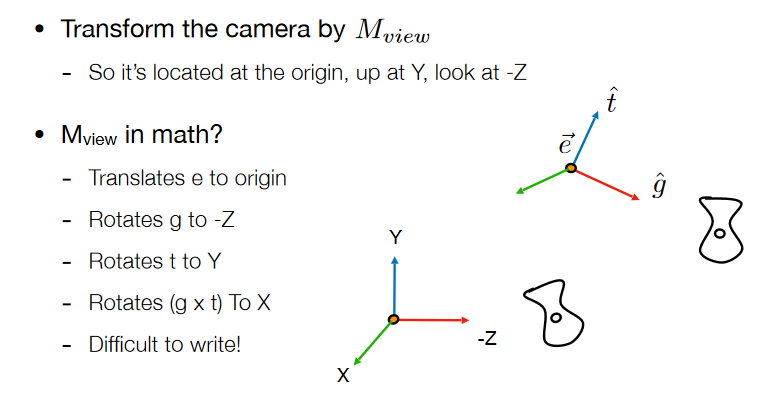
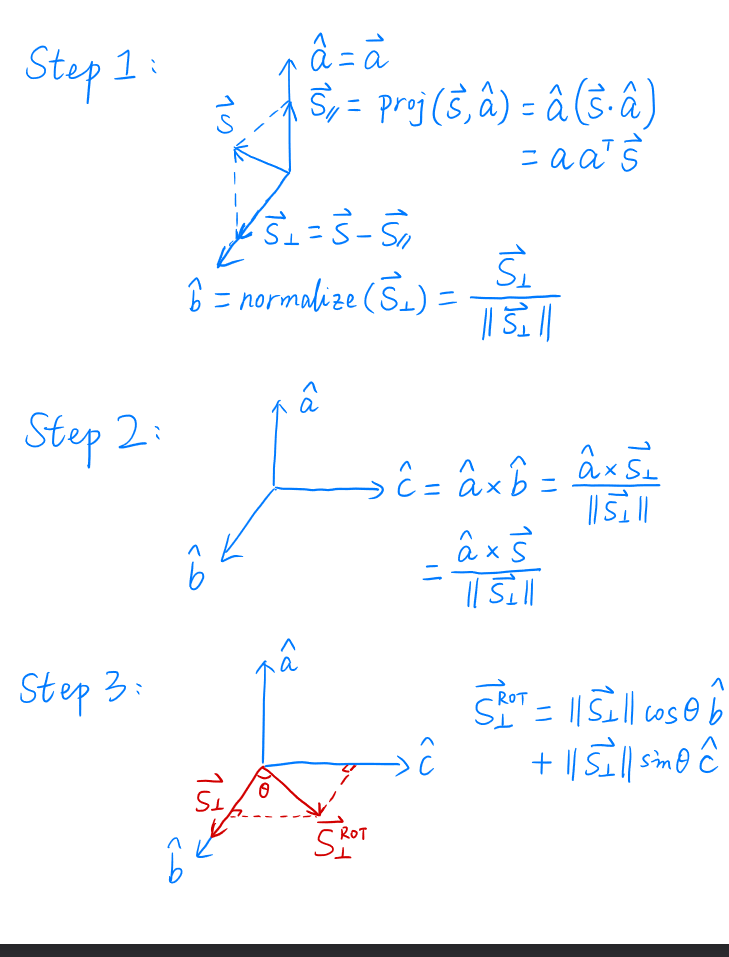
直接旋转并不好求，可以先求逆变换，而这个矩阵逆又等于矩阵转置

Projection transformation

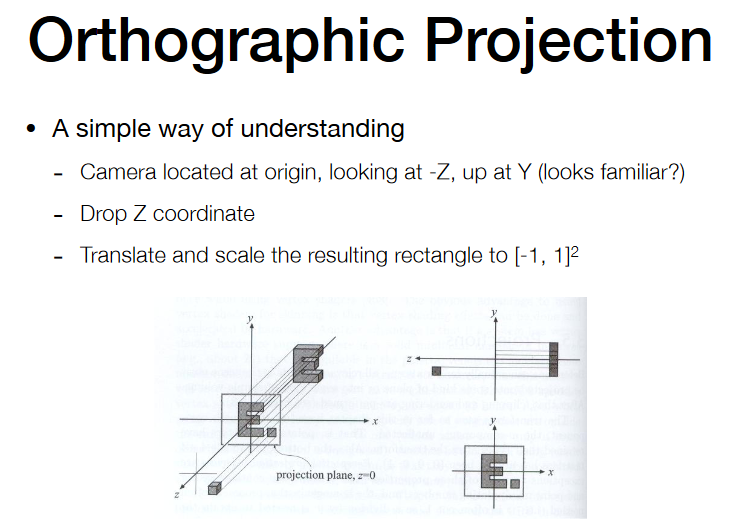
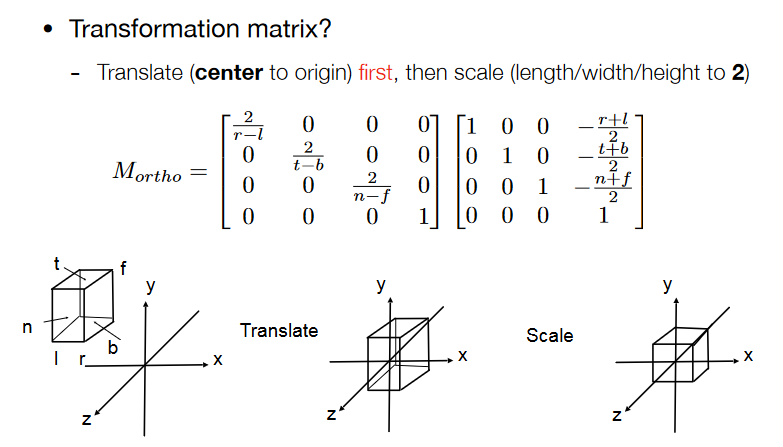
正交投影

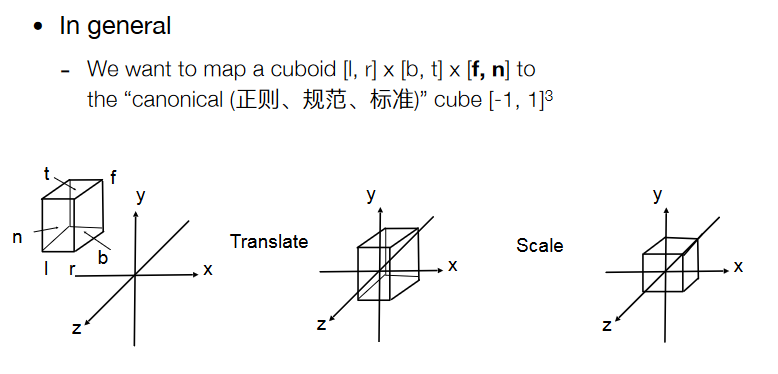
z轴上，远小于近，（相机朝-z方向看）
• Slightly different orders (to the “simple way”)

• Center cuboid by translating
• Scale into “canonical” cube
  • Caveat
• Looking at / along -Z is making near and far not intuitive (n > f)
• FYI: that’s why OpenGL (a Graphics API) uses left hand coords.

正交投影
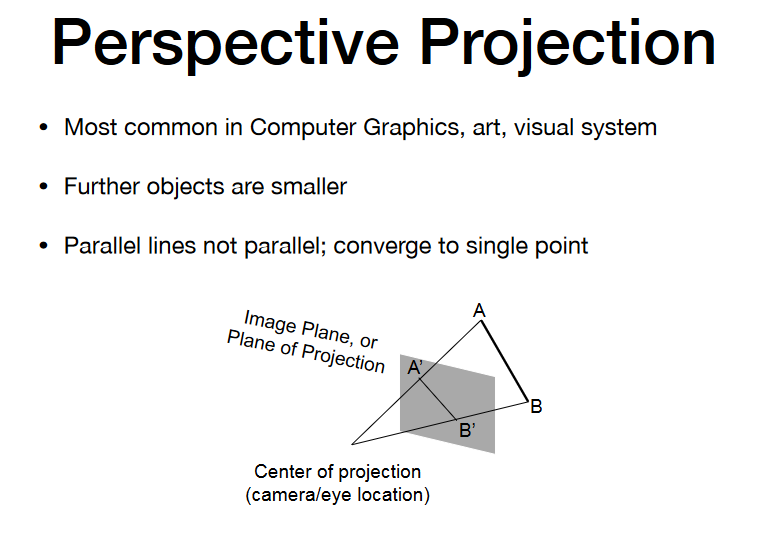• Recall: property of homogeneous coordinates

• (x, y, z, 1), (kx, ky, kz, k != 0), (xz, yz, z2, z != 0) all represent
  the same point (x, y, z) in 3D
• e.g. (1, 0, 0, 1) and (2, 0, 0, 2) both represent (1, 0, 0)
  
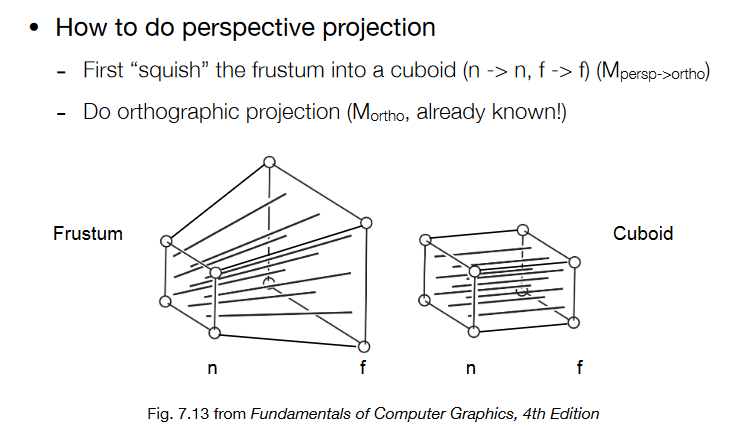
  挤压
  
  
  
  

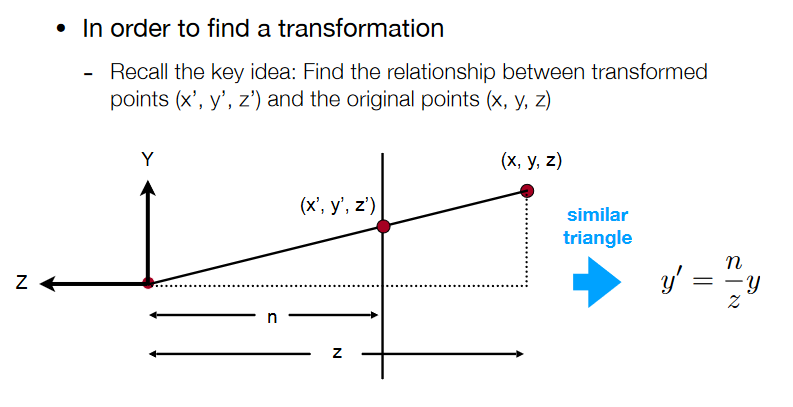
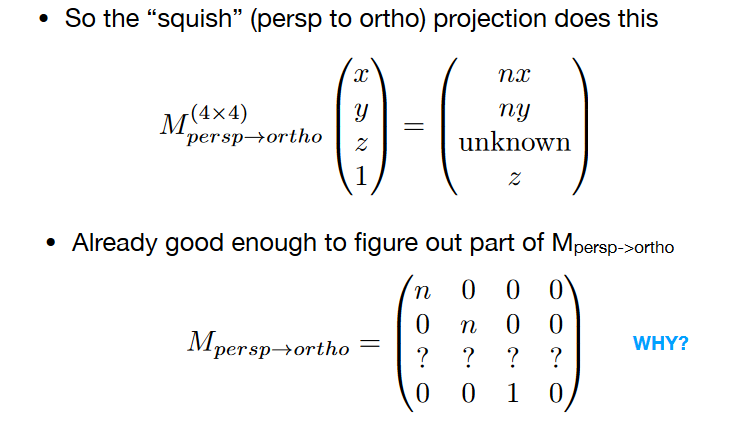
取远平面的中心点：

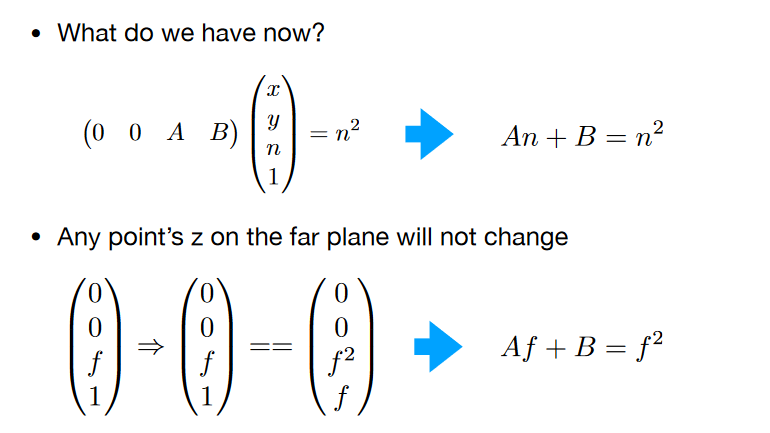
最后

以上就是洁净柜子最近收集整理的关于计算机图形学笔记1.变换向量 Vectors矩阵变换的全部内容，更多相关计算机图形学笔记1.变换向量内容请搜索靠谱客的其他文章。