文 | 陈亮
微信号 | 高速先生
相信大家已经看过了我的上篇谜一样的电容之隔直通交的处女作,弹指一挥间,一周就过去了,小陈又和大家见面了(说到小陈,大家不要误会,实在是前高速先生小陈名气太大,大家叫我小小陈也可以)。作为新人,初来乍到,在此算是正式和大家打个招呼,以后还请大家多多关照。今天我们来了解一番电容中绝缘介质的相对介电常数,可能有的小伙伴就要问了:“电容器生产出来之后,介质都固定了,我们了解电容介质的介电常数的影响又有什么作用呢?”请大家稍安勿躁,且听我慢慢道来。作为攻城狮不仅仅需要关注实际电容器,更需要关注信号传输路径中的电容。例如信号线对地平面构成的电容大小会直接影响传输线阻抗、信号线对周围信号线的电容大小会直接影响串扰等。
在影响电容量的3个主要因素中,极板面积和极板间距是很直观的。然而相对介电常数看似是固定的材料属性,但在实际场景中就比较复杂了。举个栗子:同一块使用FR4做为介质的PCB,内层的带状线上下两端介质的相对介电常数都是4,信号线感受到的相对介电常数就是材料的相对介电常数(4)。那表层的微带线呢?一面是相对介电常数是1的空气,一面是相对介电常数是4的FR4。那么表层微带线感受的有效介电常数是多少呢?这里先容我卖个关子。
首先我们得知道什么是相对介电常数:介电常数是导体间的绝缘材料增加它们之间电容量的特性。而相对介电常数就是导体被绝缘材料包围时的电容量与导体被空气包围时的电容量的比值。
相对介电常数公式如下。

当导体周围填充的是均匀介质时,导体感受到的介电常数是介质的相对介电常数,如果周围填充的是非均匀介质的时候,那么导体感受到的介电常数和两种介质的相对介电常数有关。这时电力线通过不同介电常数的介质材料时所感受到的介电常数就称为有效介电常数。
这次我们就不举栗子了,今天举大米……

以一块水稻田为例,当稻田不施肥(介质是空气),秋天能收获稻谷200斤(使用空气做介质的电容量),当使用化肥A(介质是FR4),秋天能收获稻谷800斤(使用FR4做介质的电容量). 那么化肥A的增产常数(相对介电常数)是施肥产量和不施肥产量的比值,即 800斤/200斤=4。这样大家是不是都明白了相对介电常数是怎么来的?使用一种化肥,田的实际增产常数等于化肥的相对增产常数。
那假如这块田一部分不施肥(介质是空气),一部分使用化肥A(介质是FR4),那么怎么计算这块田实际增产常数(有效介电常数)呢?计算方法如下公式。

通常有效介电常数的精确数值需要用仿真器模拟才能得出,下面提供一种使用阻抗计算软件拟合微带线感受到的有效介电常数的方法:
PCB表层的微带线,电力线会穿过空气和FR4,感受到的介电常数会不同。由于介电常数会影响电容的增幅,所以介电常数的波动也直接影响电容量。因为电感则不受介质属性影响,所以介电常数的波动的变化会直接导致阻抗的变化,根据阻抗公式:
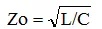
可以通过下面的方法来得到。
- 使用非嵌入式微带线模型,一面接触空气,一面接触FR4时的线路阻抗(猜想:此微带线模型内部算法是考虑了空气的,因为空气的参数固定所以没有设置选项)。

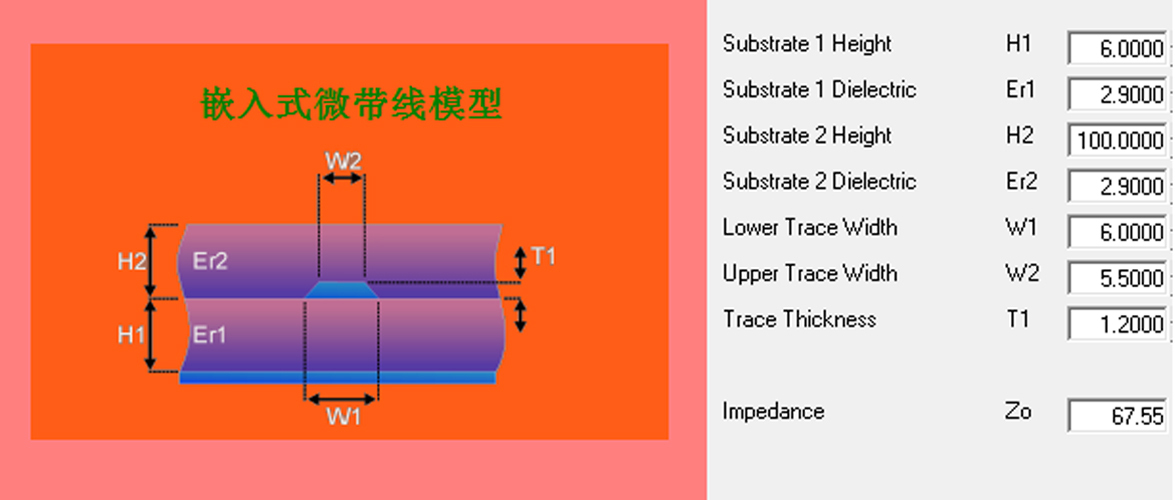
2. 使用嵌入式微带线模型,用H2模拟空气,介电常数为1,厚度尽量大,尽量包裹所有的电力线。猜想用嵌入式微带线的H2模拟空气参数得到的阻抗与非嵌入式微带线获得的阻抗一致。

根据软件计算的结果,两组模型获得的结果非常接近,证实了猜想,非嵌入微带线模型是考虑了空气影响的,实际上是一种特殊的嵌入式微带线。
3.在验证了非嵌入式微带线模型实际是一种特殊的嵌入式微带线后,我们用嵌入式微带线模型进行有效介电常数的拟合。

根据拟合结果:微带线一面接触空气,一面接触FR4时,铜厚厚度1.2MIL,如将空气和FR4看成一个整体(一块田),走线感受到的有效相对介电常数约是2.9(实际增产常数)。此方法获得的拟合结果是近似值,带状线也可以用相同方式拟合。
了解了相对介电常数对电容的影响,以及多种不同相对介电常数介质对电容的影响,有助于分析因介电常数变化引起的反射、串扰、延时等问题。其中典型就是板材的玻纤效应:PCB常用介质FR4是玻璃纤维布与环氧树脂混合成的,电力线穿过这两种介电常数不同的介质,感受到的有效介电常数就是FR4的相对介电常数。而常用的1080、106等型号的玻璃布是网格状,网格内和网格外的玻璃纤维布与环氧树脂的比例不同,且玻璃纤维布的相对介电常数高于环氧树脂的相对介电常数,导致网格内和网格外的有效介电常数不同。所以走在网格内的信号线比走在网格外的信号线感受的有效介电常数更低;同时走在网格中的信号比玻纤布上的信号更快到达,两信号线虽然等长但是并不等时。有效介电常数直接影响电容量,进而影响阻抗,阻抗的突变将引起反射,这就是我们常说的玻纤效应。
提问:关于如何避免板材的玻纤效应,你有什么好主意呢?结合自己的认识,并发挥想象力吧!小陈我先脑洞一波,如果我们能将玻璃纤维的相对介电常数做的和环氧树脂一样,网格内和网格外的有效介电常数就是一致的,是不是就不会有玻纤效应啦。
最后
以上就是跳跃荷花最近收集整理的关于常数乘以无穷大等于多少_飘忽不定的介电常数的全部内容,更多相关常数乘以无穷大等于多少_飘忽不定内容请搜索靠谱客的其他文章。








发表评论 取消回复