归并排序的实现与求逆序对数归并排序

81 阅读 0 评论 54 点赞

我是靠谱客的博主纯情百褶裙，最近开发中收集的这篇文章主要介绍归并排序的实现与求逆序对数归并排序，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

归并排序

归并排序是个一种非常有趣的算法，原理就像比武大会，比武大会需要
选出一个最厉害的武术高手，但是参与者很多很多，总不能让他们在一起
打群架吧！因此就有了擂台赛这种形式出现。
无论参赛者有多少，主办方都可以让他们两两比赛，获胜者再分成两两一组，
继续比试，一直到决出冠军

举个例子

有A、B、C、D、E、F、G、H一共8人参考参加比武大会。

第一轮，两两一组，有4名选手胜出（四分之一决赛）
第二轮，两两一组，有两名选手胜出（半决赛）
第三轮，仅剩的两人一组，冠军胜出（总决赛）

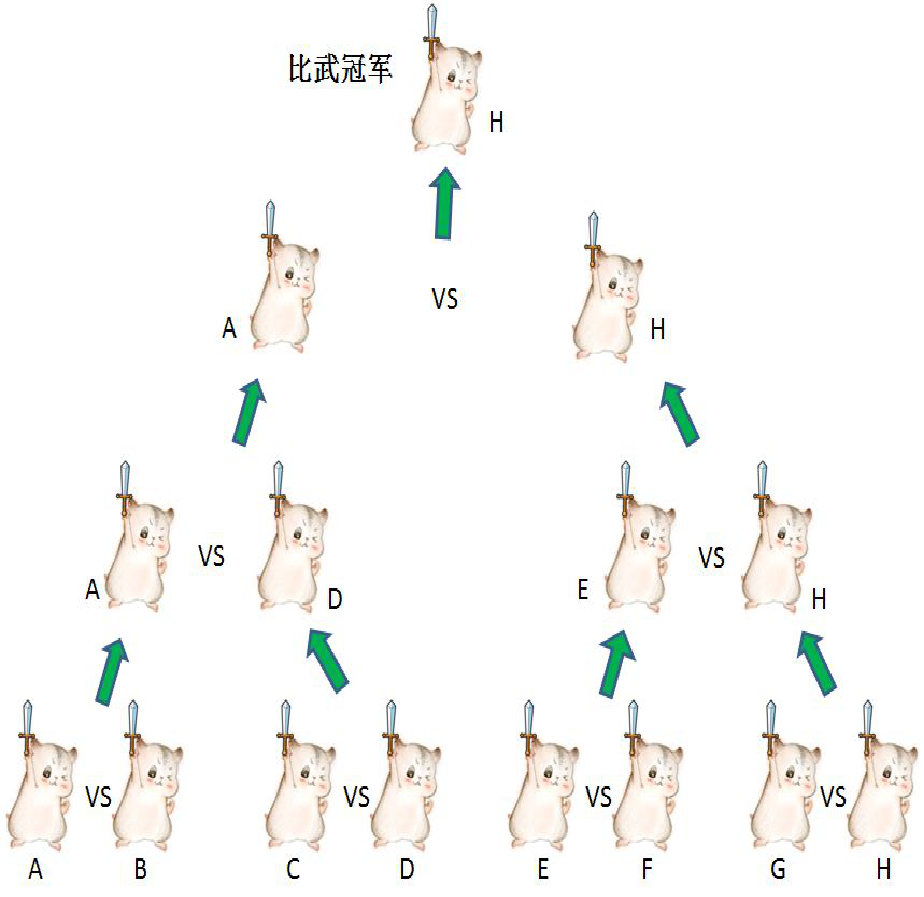
擂台赛流程：先进行两两分组竞赛，然后胜出者两两分组继续竞赛，归并排序的流程
也是类似的，但存在一些不同之处。

归并排序，分而治之，分：二分；治：合并

二分

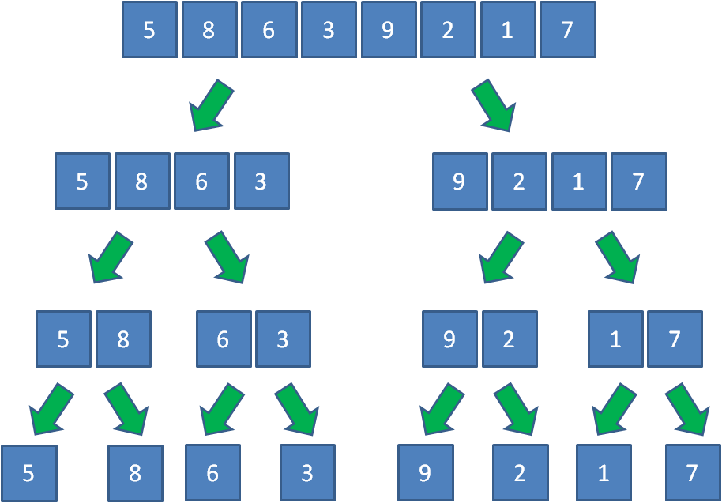
假设集合一共有n个元素，算法将会对集合进行逐层的折半分组。
第一层分成两个大组，每组n/2个元素；
第二层分成4个小组，每组n/4个元素；
…
一直到每组只有一个元素为止

在这里插入图片描述

Code:

void erfen(int l,int r)        //二分 
{
	int mid=(r - l)/2 + l;
	if(l<r)
	{
		erfen(l,mid);
		erfen(mid+1,r);
	}
	_merge(l,mid,r);
}

合并

归并排序和擂台赛有一个很大的不同，就是擂台赛只需要决定谁最大，而并不关心谁第二、第三；
而归并排序则需要确定每一个元素的排列位置。
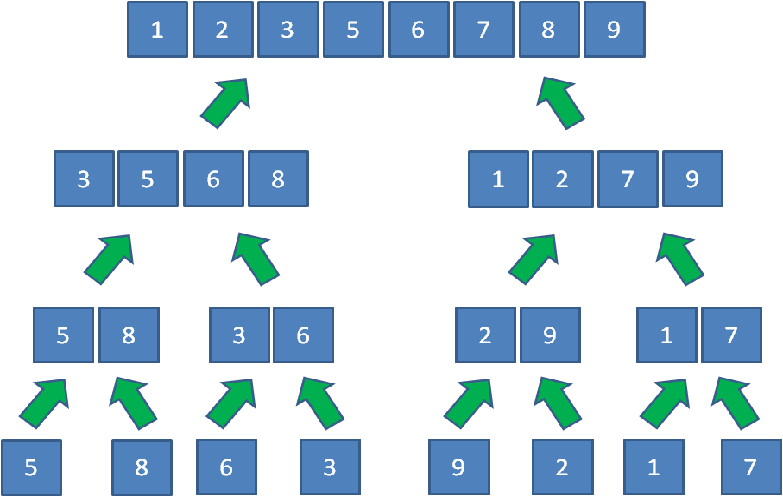
因此我们需要不断把有序的小组不断合并成更大的有序的组

实现：3个操作

实现：3个操作
创建一个额外大集合用于存储归并结果，长度是两个小集合之和。
从左到右逐一比较两个小集合中的元素，把较小的元素优先放入大集合。
从另一个还有剩余元素的集合中，把剩余元素按顺序复制到大集合尾部

在这里插入图片描述

Code

void _merge(int l,int mid,int r)//归并
{
	int p1=l,p2=mid+1;
	for(int i=l;i<=r;i++)
	{
		//两段各个数比较大小存入 
		if(((p1<=mid)&&(p2>r))||(a[p1]<a[p2]))
		{
			b[i]=a[p1];
			p1++;
		}
		else
		{
			b[i]=a[p2];
			p2++;
		}
	}
	for(int i=l;i<=r;i++)
	a[i]=b[i];
}

通过归并排序求逆序数

逆序数：在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。

例1： 3 4 1 2 逆序数为4 例2： 5 1 2逆序数为2

例1归并排序合并代码实现：

a（3,4）b（1,2）

1比3小，然后就有1比3后面的每个数小

即1与3及3后面每个数构成一个逆序对（（3,1）（4,1））。1存入，2与3比较，同理有2逆序对（（3,2 ）（4,2））。

有序组a，b （a在b前）

故当合并成有序大组时，若b[i]<a[i] , b[i]即与a[i]后面的值及a[i]构成逆序对。

这时，我们只用在归并排序的合并函数里加条赋值语句即可求出一个数组的逆序对数。

代码：

int a[100],b[200],n,ans=0;
void _merge(int l,int mid,int r)//归并
{
	int p1=l,p2=mid+1,i;
	for(i=l;p1<=mid&&p2<=r;i++)
	{
		if(a[p1]<a[p2])
		{
			b[i]=a[p1];
			p1++;
		}
		else
		{
			b[i]=a[p2];
			p2++;
			ans += mid - p1 + 1;//a[p2]和a[p1]之后及a[p1]每一个数都能组成逆序数对
		}
	}
	while(p1<=mid){b[i]=a[p1];i++;p1++;}
	while(p2<=r){b[i]=a[p2];i++;p2++;}
	for(int i=l;i<=r;i++)
	a[i]=b[i];
}