分解组件中的信号（矩阵分解问题） - 数据降维

一，主成分分析（PCA）

传送门：（无监督数据降维）主成分分析法 - PCA

1.1 精确的PCA和概率解释

PCA用于分解一组解释最大方差的连续正交分量中的多元数据集。在scikit-learn中，PCA被实现为学习的转换器对象组件使用其fit方法，并且可用于新数据以将其投影到这些组件上。

在应用SVD之前，PCA会居中，但不会缩放每个功能的输入数据。可选参数whiten=True使得可以将数据投影到奇异空间上，同时将每个分量缩放到单位方差。如果下游模型对信号的各向同性有很强的假设，这通常会很有用：例如，带有RBF内核和K-Means聚类算法的支持向量机就是这种情况。

以下是虹膜数据集的示例，该虹膜数据集由4个要素组成，投影在2个维度上，这些要素可以解释大多数差异：

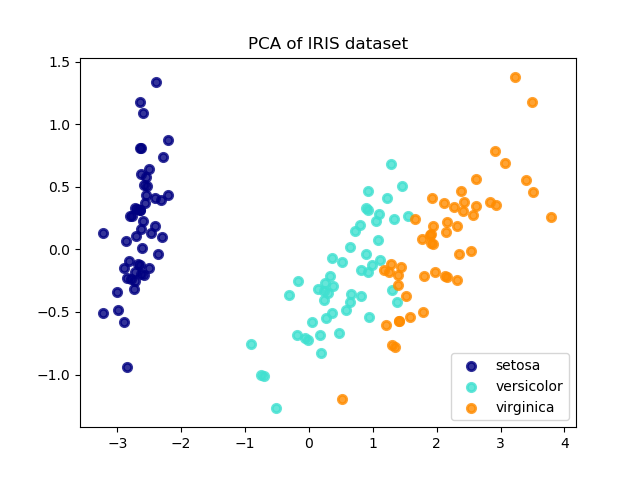
该PCA对象还提供了PCA的概率解释，该解释可以根据其解释的方差量给出数据的可能性。这样，它实现了一种可用于交叉验证的 score方法：

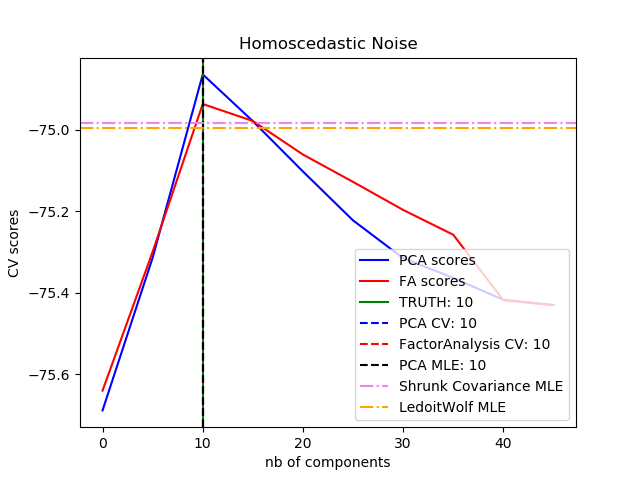
例子：

• Iris数据集的LDA和PCA 2D投影比较
• 使用概率PCA和因子分析（FA）进行模型选择

1.2 增量主成分分析

PCA对象非常有用，但是对于大型数据集有某些限制。最大的限制是PCA仅支持批处理，这意味着要处理的所有数据都必须位于主存储器中。而 IncrementalPCA对象使用不同的处理形式，并允许部分计算，这些计算几乎完全匹配PCA以小批量方式处理数据时的结果。IncrementalPCA通过以下方式可以实现核心外主成分分析：

• 使用其partial_fit方法处理从本地硬盘驱动器或网络数据库顺序获取的数据块。
• 在稀疏矩阵或内存映射文件上使用numpy.memmap

IncrementalPCA仅存储分量和噪声方差的估计值，以便按顺序explained_variance_ratio_递增。这就是为什么内存使用量取决于每批样品的数量，而不是数据集中要处理的样品数量的原因。

与中的一样PCA，IncrementalPCA在应用SVD之前，将居中但不缩放每个要素的输入数据。

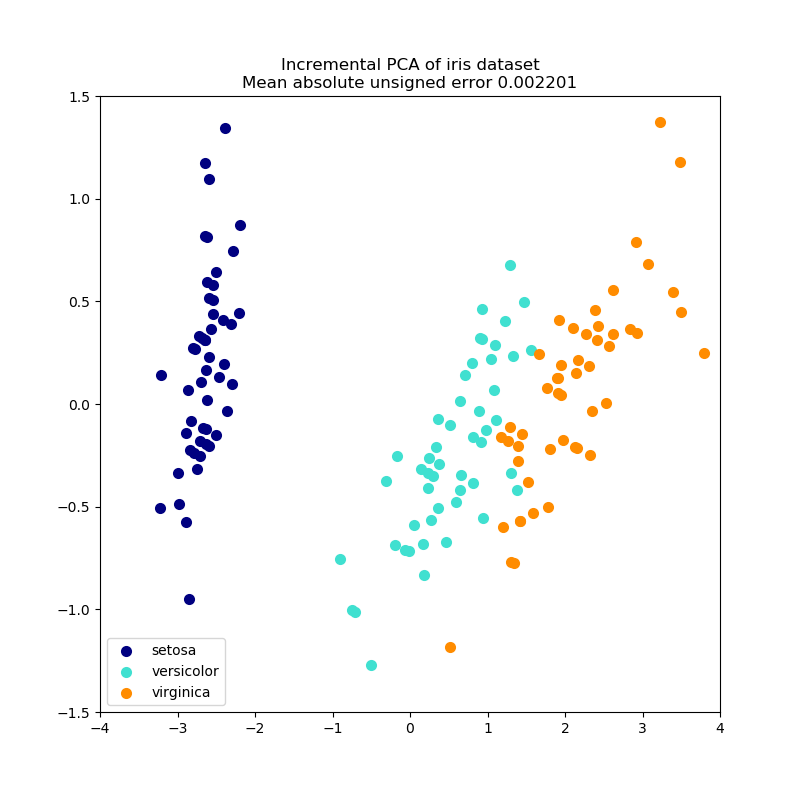
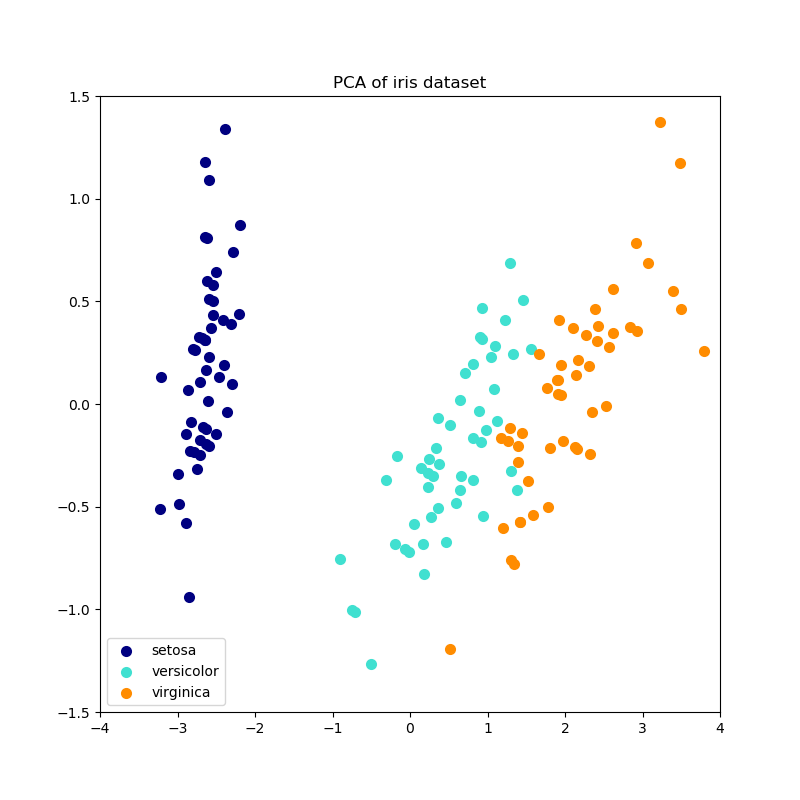
例子：

• 增量式PCA

1.3 随机SVD的主成分分析

通过删除与较低奇异值关联的分量的奇异矢量，将数据投影到保留大部分方差的低维空间通常很有趣。

例如，如果我们使用64x64像素的灰度级图片进行面部识别，则数据的维数为4096，并且在如此宽的数据上训练RBF支持向量机很慢。此外，我们知道数据的固有维数比4096低得多，因为人脸的所有图片看起来都有些相似。样本位于一个低维流形上（例如，大约200个）。PCA算法可用于线性变换数据，同时降低维数并同时保留大部分已解释的方差。

在这种情况下，与可选参数svd_solver=“randogrammed”一起使用的PCA类非常有用：因为我们将删除大多数奇异向量，所以将计算限制在对奇异向量的近似估计上会更有效，我们将继续实际执行转换。

例如，以下显示了Olivetti数据集中的16个样本肖像（以0.0为中心）。右侧是重塑为肖像的前16个奇异矢量。因为我们只需要数据集的前16个奇异矢量 n_samples = 400 和 n_features=64X64=4096，计算时间少于1s：

如果我们注意 n_max=MAX(n_samples, n_features) 和 n_min=MIN(n_samples, n_features)，随机化的时间复杂度PCA为 O(n_max² * n_components) 代替 O(n_max² * n_min) 在PCA中实现的精确方法。

随机化的内存占用PCA也与 2 * n_max² * n_components 代替 n_max² * n_min 对于确切的方法。

注：用svd_solver='randomized'在PCA中实现逆_变换不是变换的精确逆变换，即使whiten=False（默认值）。

例子：

• 使用特征脸和SVM的脸部识别示例
• 人脸数据集分解

1.4 核的主分量分析

KernelPCA是PCA的扩展，它通过使用内核来实现非线性降维。它具有许多应用，包括降噪，压缩和结构化预测（内核相关性估计）。KernelPCA同时支持 transform和inverse_transform。

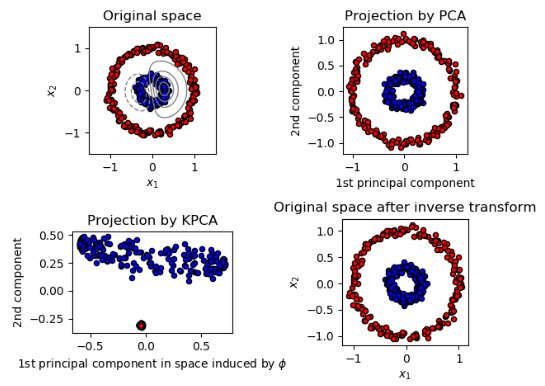
例子：

• 内核PCA - Code

1.5 稀疏主成分分析（SparsePCA和MiniBatchSparsePCA）

SparsePCA 是PCA的一种变体，其目的是提取最能重构数据的稀疏分量集。

小批量稀疏PCA（MiniBatchSparsePCA）是一种变体， SparsePCA它速度更快，但准确性较低。对于给定的迭代次数，通过迭代功能部件的小块可以达到提高的速度。

主成分分析（PCA）的缺点在于，用这种方法提取的成分仅具有密集的表达式，即当表达为原始变量的线性组合时，它们具有非零系数。这会使解释变得困难。在许多情况下，可以更自然地将真实的基础组件想象为稀疏向量；例如，在人脸识别中，组件自然可以映射到人脸的各个部分。

稀疏的主成分产生了更简洁，可解释的表示形式，清楚地强调了哪些原始特征会造成样本之间的差异。

以下示例说明了使用稀疏PCA从Olivetti人脸数据集中提取的16个分量。可以看出正则项如何诱发许多零。此外，数据的自然结构导致非零系数垂直相邻。该模型没有在数学上强制执行此操作：每个组件都是一个向量h∈R⁴⁰⁹⁶，并且没有垂直邻接的概念，除非在人类友好的可视化期间显示为64x64像素的图像。下面显示的组件显示为本地的事实是数据固有结构的影响，这使得此类本地模式将重构误差降至最低。存在一些稀疏性准则，其中考虑到了邻接关系和不同类型的结构。有关此类方法的概述。有关如何使用稀疏PCA的更多详细信息，请参见下面的“示例”部分。

请注意，稀疏PCA问题有许多不同的表述。此处实现的是基于[Mrl09]的。解决的优化问题是PCA问题（字典学习），具有 L₁ 对组件的惩罚：

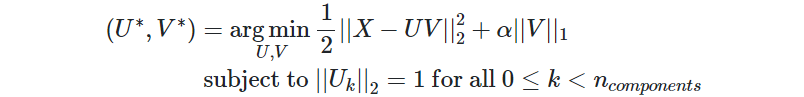
稀疏性 L₁ 当很少有训练样本可用时，规范还可以防止学习组件受到干扰。可以通过超参数来调整惩罚程度（以及稀疏程度）alpha。较小的值会导致逐渐正规化的因式分解，而较大的值会将许多系数缩小为零。

例子：

• 人脸数据集分解

二，Latent Dirichlet Allocation (LDA)

潜在狄利克雷分配是一个生成概率模型，用于收集离散数据集（例如文本语料库）。它也是一个主题模型，用于从文档集合中发现抽象主题。

LDA的图形模型是一个三级生成模型：

例子：

• 非负矩阵分解和潜在狄利克雷分配的主题提取

最后

以上就是飘逸篮球为你收集整理的分解组件中的信号（矩阵分解问题） - 数据降维的全部内容，希望文章能够帮你解决分解组件中的信号（矩阵分解问题） - 数据降维所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。