pytorch学习--线性回归

pytorch学习–线性回归

求解步骤：

• 确定模型 Module: y=wx+b

• 选择损失函数 MSE： 均方差等

• 求解梯度并更新w,b w=w-LR*w.grad b=b-LR*w.grad（LR:步长，即学习率 ）

import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)
lr=0.05
x=torch.rand(20,1)*10
y=2*x+(5+torch.randn(20,1))
#初始化 w 和 b
w=torch.randn((1),requires_grad=True)
b=torch.zeros((1),requires_grad=True)
#设置迭代次数为1000
for iteration in range(1000):
    wx=torch.mul(w,x)   # w*x
    y_pred=torch.add(wx,b)  # y_pred=w*x+b
    #计算损失值 用均方差
    loss=(0.5*(y-y_pred)**2).mean()
    # 反向传播
    loss.backward()
    #更新b和w
    b.data.sub_(lr*b.grad)
    w.data.sub_(lr*w.grad)
	# 清零张量的梯度
    w.grad.zero_()
    b.grad.zero_()


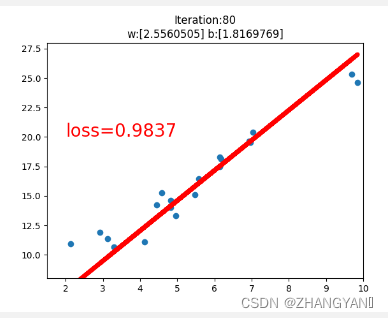
    #画图过程
    if iteration%20==0:
        plt.scatter(x.data.numpy(),y.data.numpy())
        plt.plot(x.data.numpy(),y_pred.data.numpy(),'r-',lw=5)
        plt.text(2,20,'loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'red'})
        plt.xlim(1.5,10)
        plt.ylim(8,28)
        plt.title("Iteration:{}nw:{} b:{}".format(iteration,w.data.numpy(),b.data.numpy()))
        plt.pause(1)


        if loss.data.numpy()<1:
            break;
        plt.show()

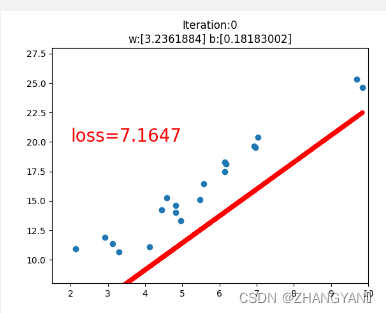
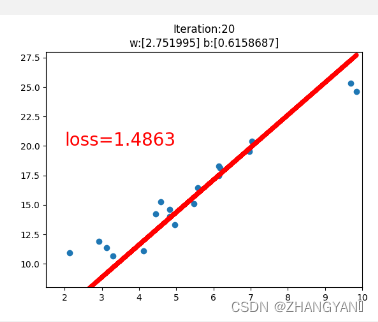
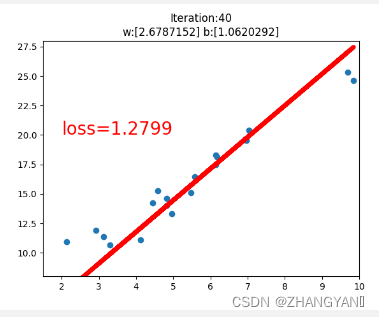
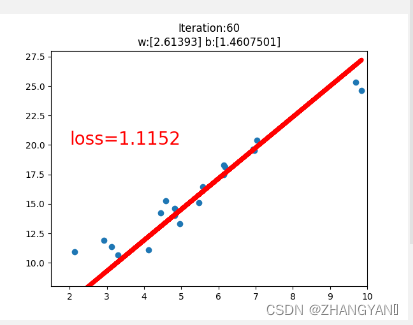
loss.backward()
故名思义，就是将损失loss 向输入侧进行反向传播，同时对于需要进行梯度计算的所有变量 (requires_grad=True)，计算梯度 d(loss)/dx，并将其累积到梯度x.grad 中备用,即:x.grad=x.grad+d(loss)/dx

关于张量清零
原因在于在PyTorch中，计算得到的梯度值会进行累加
梯度累加就是，每次获取1个batch的数据，计算1次梯度，梯度不清空，不断累加，累加一定次数后，根据累加的梯度更新网络参数，然后清空梯度，进行下一次循环。一定条件下，batchsize 越大训练效果越好，梯度累加则实现了 batchsize 的变相扩大，如果accumulation_steps 为 8，则batchsize ‘变相’ 扩大了8倍

最后

以上就是苗条芝麻为你收集整理的pytorch学习--线性回归的全部内容，希望文章能够帮你解决pytorch学习--线性回归所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。