文章目录
- 普通实现
- 准备数据
- 反向传播
- 构建模型 实现
- 实例化模型、损失函数、优化器
- 训练数据
- 评估模型
普通实现
准备数据
import torch
import matplotlib.pyplot as plt
# 1、准备数据
# y = 2 * x + 0.8
x = torch.rand([500, 1])
y_true = 2 * x + 0.8
# 2、通过模型计算 y_predict
w = torch.rand([1, 1], requires_grad=True)
b = torch.tensor(0, requires_grad=True, dtype=torch.float32)
learning_rate = 0.01
反向传播
# 4、通过循环,反向传播,更新参数
for i in range(1000):
y_predict = torch.matmul(x, w) + b # 预测值
# 3、计算loss
# 回归问题,使用均方误差
loss = (y_true - y_predict).pow(2).mean()
if w.grad is not None:
w.grad.data.zero_()
if b.grad is not None:
b.grad.data.zero_()
loss.backward() # 反向传播
w.data = w.data - learning_rate * w.grad
b.data = b.data - learning_rate * b.grad
if i%100 == 1:
print(f'-- i: {i}, w : {w.item()}, b : {b.item()}, loss : {loss}, ')
print(f'-- end w : {w.item()}, b : {b.item()}, loss : {loss}, ')
-- i: 1, w : 0.35467997193336487, b : 0.06384684145450592, loss : 2.716614007949829,
-- i: 101, w : 1.0814398527145386, b : 1.1525230407714844, loss : 0.08122585713863373,
-- i: 201, w : 1.238681674003601, b : 1.1865873336791992, loss : 0.049526866525411606,
-- i: 301, w : 1.3382785320281982, b : 1.1438771486282349, loss : 0.03770563006401062,
-- i: 401, w : 1.4222863912582397, b : 1.1008449792861938, loss : 0.028764590620994568,
-- i: 501, w : 1.4954265356063843, b : 1.0628066062927246, loss : 0.021944044157862663,
-- i: 601, w : 1.5592910051345825, b : 1.029546856880188, loss : 0.016740744933485985,
-- i: 701, w : 1.61506986618042, b : 1.0004940032958984, loss : 0.012771294452250004,
-- i: 801, w : 1.6637893915176392, b : 0.9751182794570923, loss : 0.009743028320372105,
-- i: 901, w : 1.7063422203063965, b : 0.9529542922973633, loss : 0.007432833779603243,
-- end w : 1.7428138256072998, b : 0.9339574575424194, loss : 0.005701201036572456,
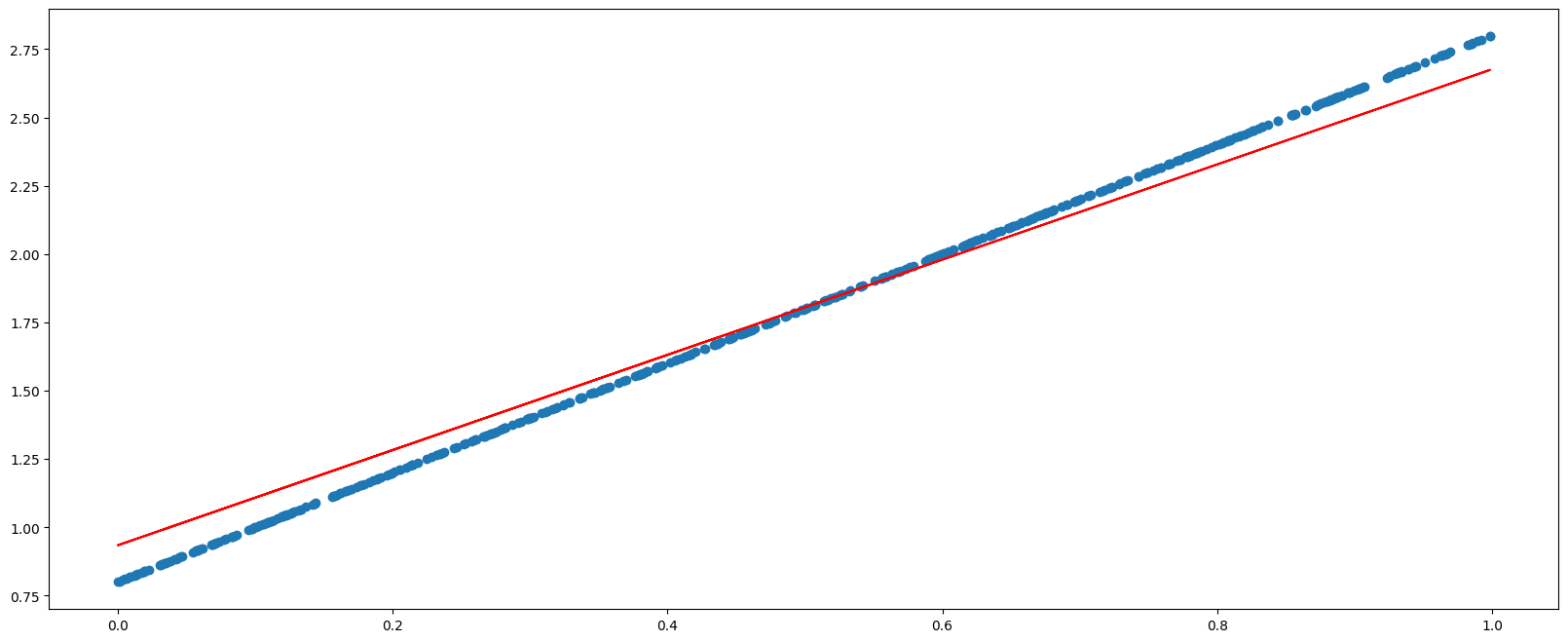
plt.figure(figsize=(20, 8))
plt.scatter(x.numpy().reshape(-1), y_true.numpy().reshape(-1))
y_predict = torch.matmul(x, w) + b
plt.plot(x.numpy().reshape(-1), y_predict.detach().numpy().reshape(-1), c='r')
plt.show()
测试
x1 = torch.tensor(2)
y1 = w * x1 + b
x1, y1
(tensor(2), tensor([[4.4196]], grad_fn=<AddBackward0>))
构建模型 实现
import torch
from torch import nn
from torch import optim # 优化器
构建数据
x = torch.rand([500, 1])
y_true = 2 * x + 0.8
构建模型
1、需要调用super方法,继承父类的属性和方法
2、必须实现 forward 方法,用来定义我们网络的前向计算过程。
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
# 预定义好的线性模型,也被称为 全链接层
# 传入的参数为输入的数量、输出的数量(in_features, out_features);是不算 batch_size 的列数。
# nn.Module 定义了 __call__ 方法,实现的就是 调用 forward 方法,即 LR 的实例,能够直接被传入参数调用;实际调用的是 forward 方法。
self.linear = nn.Linear(1, 1)
def forward(self, x):
out = self.linear(x)
return out
实例化模型、损失函数、优化器
model = LR() # 实例化模型
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
'''
SGD (
Parameter Group 0
dampening: 0
foreach: None
lr: 0.001
maximize: False
momentum: 0
nesterov: False
weight_decay: 0
)
'''
优化器类 optimizer,可以理解为 torch 为我们封装的 用来更新参数的方法。
比如:常见的随机梯度下降(stochastic gradient descent, SGD) 优化器类都是由 torch.optim 提供的,例如:
- torch.optim.SGD
- torch.optim.Adam
注意, 1、可以使用 model.parameters() 来获取参数;获取模型中 所有 requires_grad = True 的参数;
2、优化类的使用发发: 1)实例化; 2)所有参数的梯度,将其值置为0; 3)反向传播计算梯度; 4)更新参数值
训练数据
for i in range(10000):
# 传入数据,计算结果
y_predict = model(x)
# y_predict = model(x_true) # 向前计算预测值
loss = criterion(y_true, y_predict) # 调用损失函数,传入真实值和预测值,得到损失结果
optimizer.zero_grad() # 当前循环参数梯度置为 0
loss.backward() # 计算梯度
optimizer.step() # 更新参数的值
if i%1000 == 0:
print(f'-- {i} {loss.data}')
-- 0 5.0724568367004395
-- 1000 0.2791365087032318
-- 2000 0.19754908978939056
-- 3000 0.1544567495584488
-- 4000 0.12085574865341187
-- 5000 0.0945650264620781
-- 6000 0.07399351894855499
-- 7000 0.05789710581302643
-- 8000 0.04530230164527893
-- 9000 0.035447314381599426
评估模型
model.eval()
predict = model(x) # 设置模型为评估模式,即预测模式
predict = predict.data.numpy()
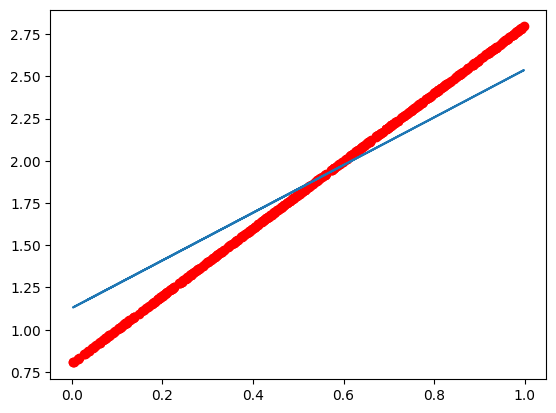
plt.scatter(x.data.numpy(), y_true.data.numpy(), c='r')
plt.plot(x.data.numpy(), predict)
plt.show()
伊织 2022-12-10
最后
以上就是大气皮皮虾最近收集整理的关于PyTorch - 线性回归的全部内容,更多相关PyTorch内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复