对视觉slam十四讲李群和李代数一章程序的学习,参考链接如下:
https://www.icxbk.com/article/detail/1313.html(最后的代码写的很好,相比于书中代码调试的更全,推荐)。
Sophus库编程基础 - 掘金
Sophus 李群 --[SO3]_luoshi006的博客-CSDN博客
一、理论
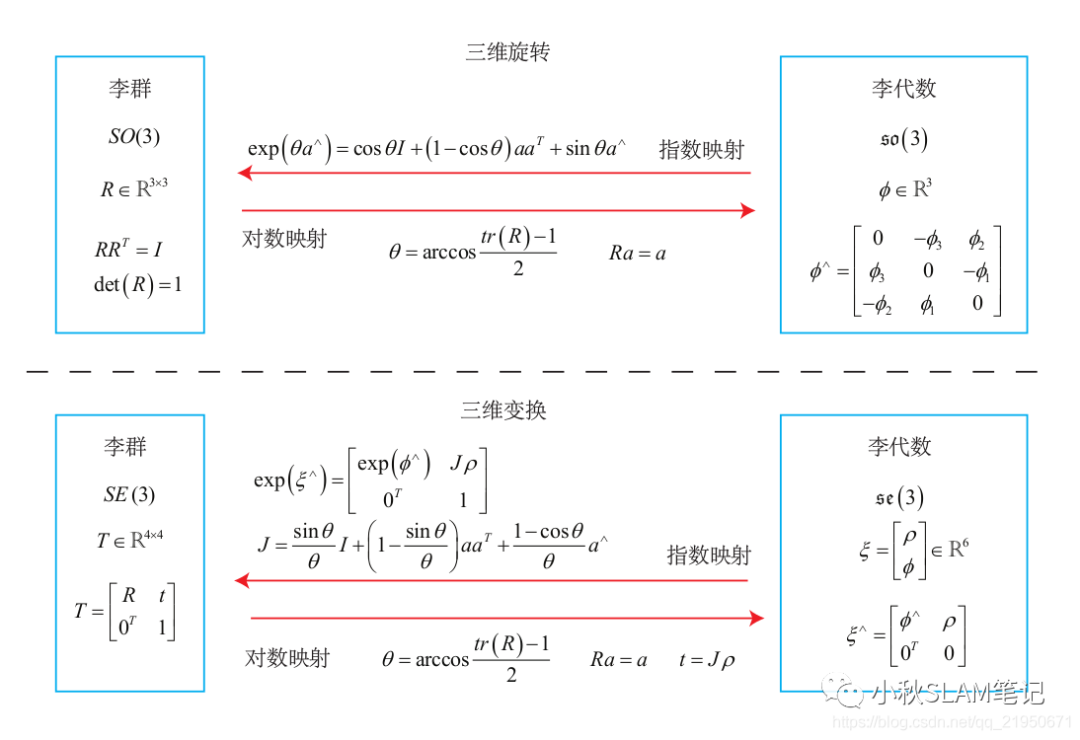
相机旋转——>旋转矩阵相乘——>李群的乘法(李群是无约束的)——>李代数的加法
对李代数的求导
二、程序
十四讲中的程序
1. eigen库,定义旋转矩阵
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();2. 初始化李群SO(3)
三维旋转矩阵构成了特殊正交群SO(3)。
李群是具有连续光滑性质的群。
可通过以下方式初始化李群:
(1)旋转矩阵
(2)旋转矢量
(3)四元数
SO3();
SO3(const SO3 & other);
SO3(const Matrix3d & _R);
SO3(const Quaterniond & unit_quaternion);
SO3(double rot_x,
double rot_y,
double rot_z);例子如下,这里需要注意的是用旋转矢量初始化的时候,不能用A1=(0,0,pi/2),SO3(A1)的形式。
Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造
Sophus::SO3 SO3_v( 0, 0, M_PI/2 ); // 亦可从旋转向量构造
Eigen::Quaterniond q(R); // 或者四元数
Sophus::SO3 SO3_q( q );
// 上述表达方式都是等价的这里输出SO(3)的时候,实际上是以so(3)形式输出,并且其输出的值和旋转矢量相对应,即李代数就是旋转矢量。

3 定义李代数so(3)
// 使用对数映射获得它的李代数
Eigen::Vector3d so3 = SO3_R.log();
cout<<"so3 = "<<so3.transpose()<<endl;
// hat 为向量到反对称矩阵
cout<<"so3 hat=n"<<Sophus::SO3::hat(so3)<<endl;
// 相对的,vee为反对称到向量
cout<<"so3 hat vee= "<<Sophus::SO3::vee( Sophus::SO3::hat(so3) ).transpose()<<endl; 4 Sophus库常用函数总结
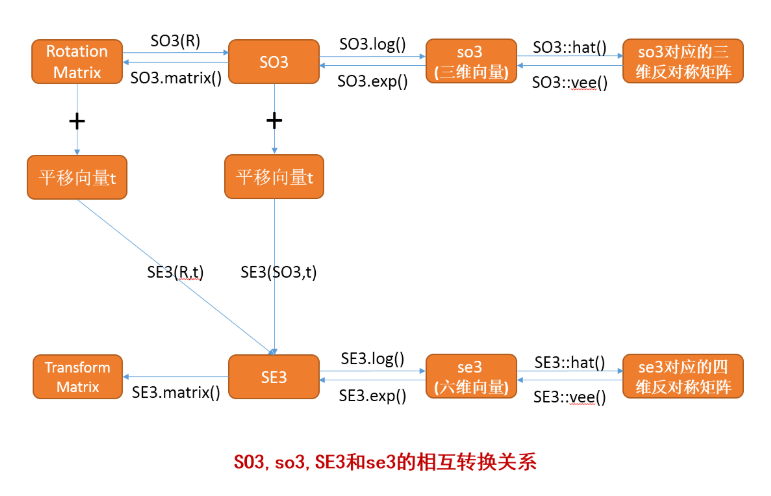
图片来源:https://www.icxbk.com/article/detail/1313.html
5. 重点:增量扰动模型的更新!
Eigen::Vector3d update_so3(1e-4, 0, 0); //假设更新量为这么多
//SO3::exp()是从三维向量到李群的函数,见上面的图
Sophus::SO3 SO3_updated = Sophus::SO3::exp(update_so3)*SO3_R;
cout<<"SO3 updated = "<<SO3_updated<<endl;
6. SE(3)
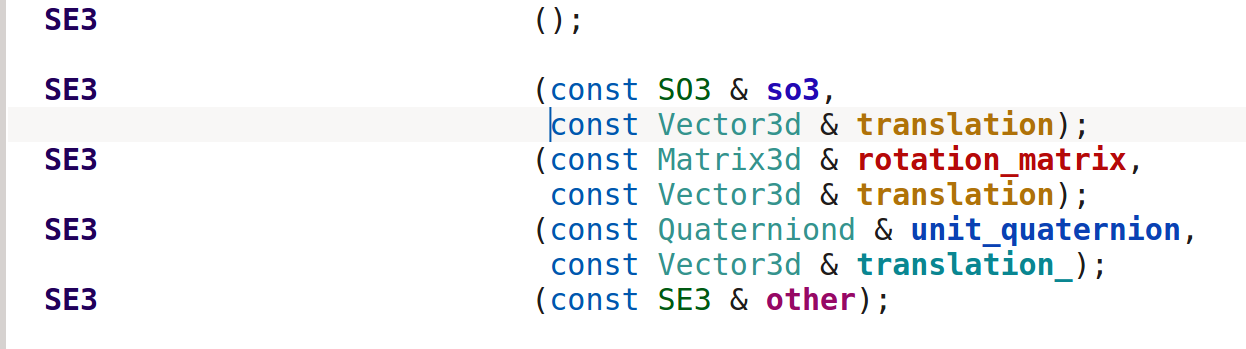
根据se3.h文件,构建方法为:
(1)SO3和平移矢量
(2)旋转矩阵和平移矢量
(3)单位四元数表示的旋转和平移矢量
Eigen::AngleAxisd A2(M_PI/2,Eigen::Vector3d(0,0,1));
Eigen::Matrix3d R2=A2.matrix();
Eigen::Quaterniond Q2(A2);
Sophus::SO3 SO3_2(R2);
Eigen::Vector3d t(1,0,0);
//初始化
Sophus::SE3 SE_Rt(R2,t);
Sophus::SE3 SE_Qt(Q2,t);
Sophus::SE3 SE_St(SO3_2,t);
注意:
尽管SE(3)是对应一个4*4的矩阵,但是输出SE(3)时是以一个六维向量输出的,其中前三位为对应的so3(旋转矢量),后3维度为实际的平移量t,而不是se3中的平移分量。

7. se(3)
代码见:https://www.icxbk.com/article/detail/1313.html
其中se(3)为:
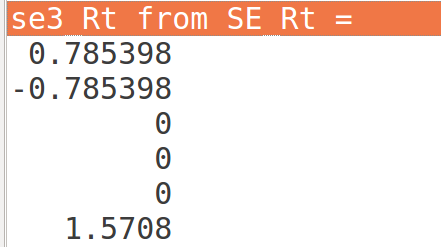
前三维不等于平移向量???
注意:se(3)对应的反对称矩阵是四维的



8. 增量扰动模型的更新
代码见:https://www.icxbk.com/article/detail/1313.html

只有平移向量
旋转之后的李群为:
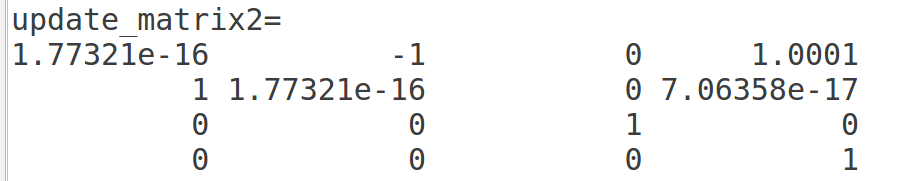
9. 问题
se(3)结果中的平移向量还没有理解???
最后
以上就是独特毛巾最近收集整理的关于C4 李群和李代数 程序调试对视觉slam十四讲李群和李代数一章程序的学习,参考链接如下:一、理论二、程序的全部内容,更多相关C4内容请搜索靠谱客的其他文章。








发表评论 取消回复