通过前序遍历，后序遍历，中序遍历的任意两种建立一棵树（对数组指针的运用）

92 阅读 0 评论 61 点赞

我是靠谱客的博主清爽灰狼，最近开发中收集的这篇文章主要介绍通过前序遍历，后序遍历，中序遍历的任意两种建立一棵树（对数组指针的运用），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

二叉树的遍历主要有三种：

（1）先(根)序遍历（根左右）

（2）中(根)序遍历（左根右）

（3）后(根)序遍历（左右根）

举个例子：

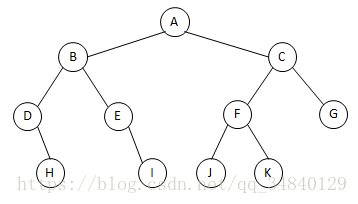
在这里插入图片描述

先(根)序遍历（根左右）：A B D H E I C F J K G

中(根)序遍历（左根右） : D H B E I A J F K C G

后(根)序遍历（左右根） : H D I E B J K F G C A

以后(根)序遍历为例，每次都是先遍历树的左子树，然后再遍历树的右子树，最后再遍历根节点，以此类推，直至遍历完整个树。

此外，还有一个命题：给定了二叉树的任何一种遍历序列，都无法唯一确定相应的二叉树。但是如果知道了二叉树的中序遍历序列和任意的另一种遍历序列，就可以唯一地确定二叉树。标记文本

例题：

7-8 玩转二叉树 (25分)

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：
输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。
层序遍历就是bfs（先左再右）

输入样例：
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：
4 6 1 7 5 3 2

对比前序遍历和中序遍历可以发现一个规律，前序遍历的第一个是根结点，在中序遍历的序列中找到这个根节点，这个点左边的所有数都属于这个根节点的左子树，右边的所有数都属于这个根节点的右子树。递归进行这个操作，每次将序列分成两部分。

以下是代码：

// 前 + 中
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define endl 'n'
#define ll long long
using namespace std;

const int N = 1e5 + 10;

int zx[150], qx[150], a[150], cnt;

struct node
{
	int l, r;
}T[N];

queue<int> Q;

int creat(int zt, int zw, int qt, int qw)
{
	if(zt > zw) return 0;   //如果zt > zw，说明已经无法再分了。
	int x = qx[qt];   //当前的根节点。qt为当前前序遍历的头
	int i = zt;  //当前的中序序列的头
	while(zx[i] != x) i ++;
	int len = i - zt;   // 左子树包含的数的个数。
	T[x].l = creat(zt, i - 1, qt + 1, qt + len);  //左子树
	T[x].r = creat(i + 1, zw, qt + len + 1, qw);  //右子树
	return x;   //返回当前根节点
}

void bfs(int root)  //bfs进行层序遍历
{
	Q.push(root);
	while(!Q.empty())
	{
		int x = Q.front();
		Q.pop();
		a[cnt ++] = x;
		if(T[x].r)	Q.push(T[x].r);
		if(T[x].l) 	Q.push(T[x].l);
	}
}

void solve()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i ++)
		cin >> zx[i];
	for(int i = 1; i <= n; i ++)
		cin >> qx[i];
	int x = creat(1, n, 1, n);
	bfs(qx[1]); 
	for(int i = 0; i < cnt; i ++)
	{
		cout << a[i];
		if(i !=  cnt - 1) cout << " ";
	}
}

int main()
{
	solve();
	return 0;
}

//后 + 中
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define endl 'n'
#define ll long long
using namespace std;

const int N = 1e5 + 10;

int zx[150], hx[150], a[N], cnt;

struct node
{
	int l, r;
}T[N];

queue<int> Q;

int creat(int zt, int zw, int ht, int hw)
{
	if(zt > zw) return 0; 
	int x = hx[hw];   
	int i = zw; 
	while(zx[i] != x) i --; 
	int len = zw - i;   
	T[x].l = creat(i + 1, zw, hw - len, hw - 1);  
	T[x].r = creat(zt, i - 1, ht, hw - len - 1);  
	return x;   
}

void bfs(int root) 
{
	Q.push(root);
	while(!Q.empty())
	{
		int x = Q.front();
		Q.pop();
		a[cnt ++] = x;
		if(T[x].r)	Q.push(T[x].r);
		if(T[x].l) 	Q.push(T[x].l);
	}
}

void solve()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i ++)
		cin >> hx[i];
	for(int i = 1; i <= n; i ++)
		cin >> zx[i];
	int x = creat(1, n, 1, n);
	bfs(hx[n]); 
	for(int i = 0; i < cnt; i ++)
	{
		cout << a[i];
		if(i !=  cnt - 1) cout << " ";
	}
}

int main()
{
	solve();
	return 0;
}