三十天挑战数据结构（13）几种内部排序方法的通俗解释

1. 简单排序
   顾名思义最简单的排序方式，包括除了希尔排序之外的所有插入排序、冒泡排序和简单选择排序。其所需平均时间为O(n^2)，辅助存储为O(1)。
   **A. 直接插入排序：**在建立存储数据结构的时候便一个一个插入来建立，按照大小关系让每个数据起初就处于它“该在的位置”。或是若原先就有一个数据组，需要插入一些新的数据，则将这些数据插入到它应该在的位置。
   **B. 2-路插入排序：**可以理解有一个循环链表，将数据依次插入进去，比标记点大的插入到标记点右边的序列，反之插入左边的序列，再重复该过程最后让这些数据都插入合适的位置。所谓2-路我理解的就是除了原先存储数据的数组之外还需要单独建一个存储结构吧。
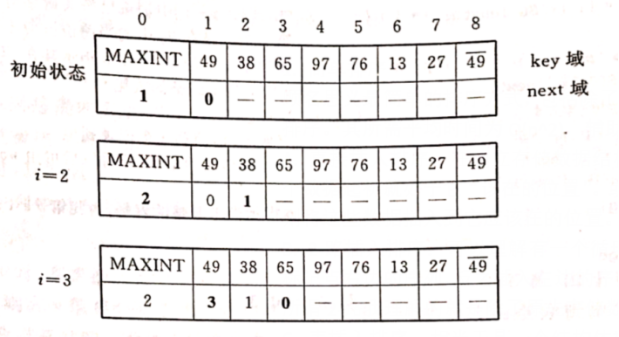
   **C. 表插入排序：**相当于是一个结构体数组，存放对应的数据和指向比它大的下一个的数据的指针。0号位置存放MAXINT，所有数据中最大的那个对应指针指向它，并且它指向整个数组中最小元素。可以用教材上的一张图比较直观地看出来：
   
   **D. 冒泡排序：**最好理解的一种排序算法，就好像冒泡一样，一个排列好的数组从第一个开始看起，如果大于它后面的那个就让它往后移一位，一直这样下去，移到最后又开始返回下一个数据继续冒泡…最终可以得到排序好的数组。
   **E. 简单选择排序：**最简单的一种交换排序，从第一个数据开始，和它之后的所有数据进行筛选，选出最小的那个数据和第一个交换位置，此时最小值便已经位于第一个位置上了；再从第二个开始…如此这样达到所有数据的排序。

2. 快速排序
   是对冒泡排序的一种改进，通过选中一个“标杆”来将整组数据分为两部分：大于它的和不大于它的，再对这两部分数据分别进行快速排序，直到排序范围缩小到一两个数据，便可直接判断交换位置。这时整组数据已经按照一定顺序排好了。
   快速排序的时间复杂度为O(nlogn)，最坏情况的时间需要O(n^2)，另需要辅助存储的空间为O(logn)。

3. 归并排序
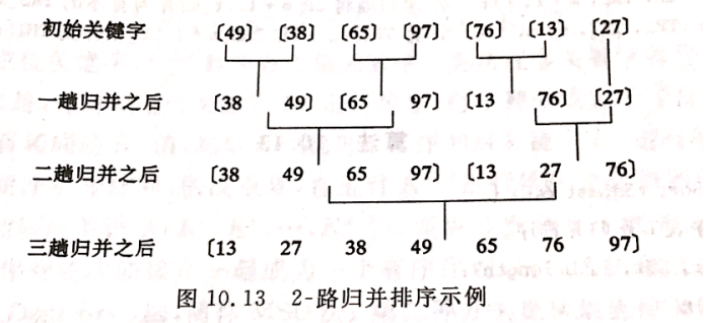
   归并排序是将两个或两个以上的有序表合成一个新的有序表。将数据均分为两个一组，再四个一组，再八个一组…如此每一趟归并都能将组内排序出来，最终合并成整个排序好的数组。
   归并排序的时间复杂度也是O(nlogn)，最坏情况的时间也是O(nlogn)，另外需要辅助存储空间为O(n)。
   还是放一张教材的图帮助理解：
   

4. 基数排序
   基数排序可以理解成一种关键字排序，每个元素可能含有多个关键字，这几个关键字有优先级的差距，在优先级相同的情况下再去比较下一优先级的关键字。
   基数排序的时间复杂度为O(d(n+rd))，需要辅助存储空间O(rd)，其中d为关键字数量，rd为关键字的取值范围。
   书上作业题的例子非常好帮助理解，便是通过基数排序来对数字进行排序，要做到其实就是将个位十位百位看做三个关键字，优先级：百位 > 十位 > 个位，列出表：
   
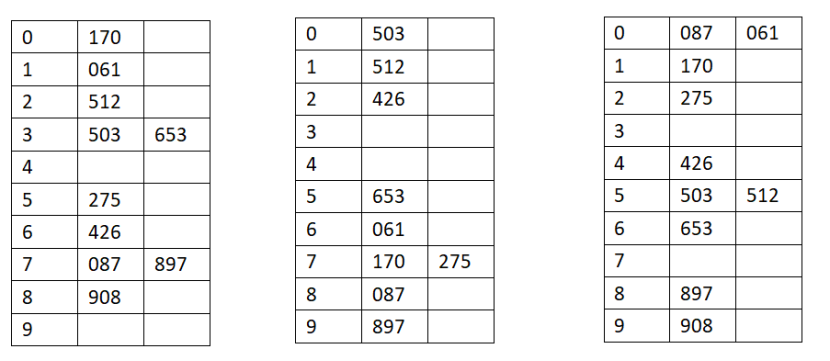
   再然后就可以很容易地得出排序：061 < 087 < 170 < 275 < 426 < 503 < 512 < 653 < 897 < 908

堆排序还没有太想明白了，所以可能拖一拖再来写，待我去问问同学们或者大佬们有没有可以指点一下的？欢迎和我一起讨论！

以上是我自己对几种排序的一个比较通俗的理解，如果有不妥的地方请指正！

最后

以上就是清爽嚓茶为你收集整理的三十天挑战数据结构（13）几种内部排序方法的通俗解释的全部内容，希望文章能够帮你解决三十天挑战数据结构（13）几种内部排序方法的通俗解释所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。