1.Linear regression with one variable——Gradient descent
通过昨天的学习,了解到了假设函数(hypothesis function),而且也有一种方法来衡量这个函数对于数据的适应性怎样。下面就需要估计假设函数中的参数,所以引进了梯度下降算法(Gradient Descent)。
1.1Gradient Descent介绍
假设我们有函数,J(θ0,θ1),想要取θ0和θ1的值,使J最小
Outline:
- Start with some θ0,θ1
- Keep changing θ0,θ1 to reduce J(θ0,θ1) until we hopefully end up at a minimum
把θ0放在x轴上,θ1在y轴上,成本函数在z轴上。绘成的图如下图所示。
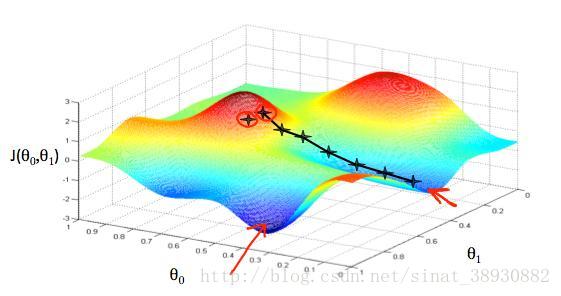
如图所示,随着θ0和θ1的变化,成本函数J可以用matlab画成彩色图,形成一个个小山包或者低谷。图上的黑点是假设我们从山上最高点出发,如果每次都沿着下降速度最快的方向下山,可以快速的达到图像中最凹陷的地方。通过数学中微积分和导数的知识可以知道,梯度的方向就是当前点下降最快的方向,所以每次都计算出所在位置的梯度,从而可以快速下山。我们每次都以下降速度最快的方向下山,同时规定好每一次下山的步伐大小,也就是被称为学习速率的α。图中,每两个黑点之间的距离就是由α确定的每次的步长。较小的α将导致较小的步长,较大的α导致较大的步长。
但是,梯度下降算法也有缺点。当你沿着梯度方向下降的时候,你是仅根据当前位置进行判断从而下降,可能不能达到全局最低点,只是达到局部最低点。而当你换一个位置的时候,你就可能达不到这个点,而达到另一个局部最低点。如图中所示的山顶的两个位置和所分别达到的最低点。
1.2Gradient descent algorithm步骤
repeat until convergence
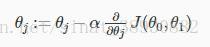
其中,j = 0,1表示特征索引号
注意:在每次迭代j中,应同时更新参数θ1,θ2,…,θn。如果在第j(th)次迭代计算另一个参数之前,更新了一个特定的参数,会导致错误。如下图所示。

注意:我们还需要调整参数α,以确保梯度下降算法在合理的时间内收敛。如下图所示,如果α太小了,梯度下降的可能就会慢;而如果α太大了算法可能就不收敛。
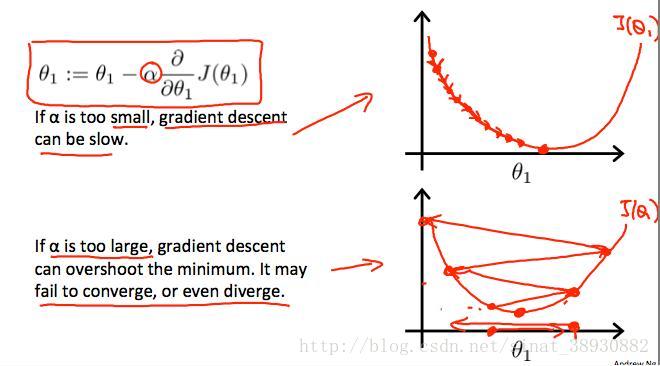
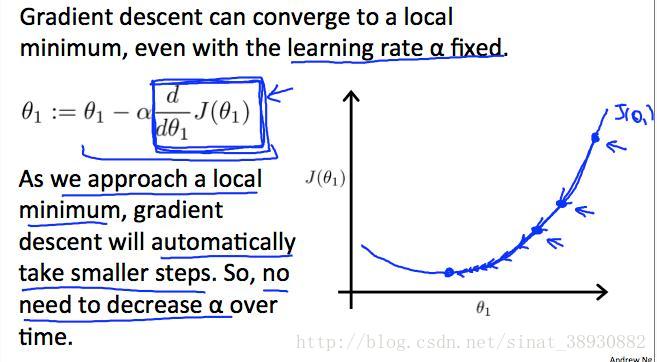
1.3Gradient Descent For Linear Regression
当梯度下降算法应用到线性回归中,我们能够推导出一种新的算法等式,如下图。
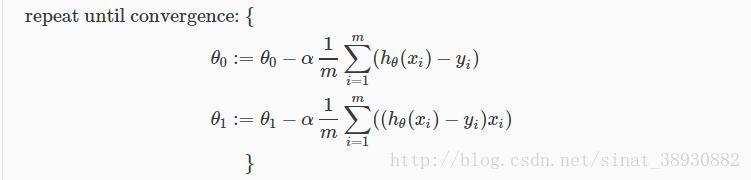
其中,m是训练集,θ0,θ1的值同时更新,xi和yi就是给定的训练集中的值,也就是数据。
注意到,上图中,把θj分为θ0,θ1,;而且对于θ1,我们在公式后面乘上一个xi。推导公示如下图。
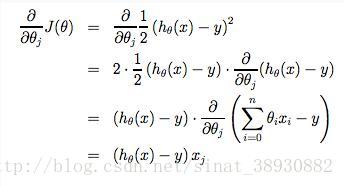
如果我们从给定的假设开始,然后重复应用这些梯度下降方程,我们的假设将变得越来越准确,接近真实值。这是对于成本函数J的梯度下降。这种方法使用到了整个训练集中的每个数据,称为批量梯度下降。注意,虽然梯度下降一般容易受到局部极小值的限制,但我们在此提出的线性回归的优化问题只有一个全局,没有其他局部最优;因此梯度下降总是收敛(假设学习速率α不是太大)到全局最小值。
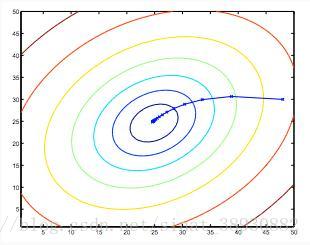
上面所示的椭圆是一个二次函数的轮廓。同时显示了由(48,30)开始使用梯度下降所采取的轨迹。图中的x(通过直线连接)标记梯度下降经过的θ的连续值,直到它收敛到最小值。
最后
以上就是不安日记本最近收集整理的关于Coursera机器学习第一周学习笔记(二)——Gradient descent1.Linear regression with one variable——Gradient descent的全部内容,更多相关Coursera机器学习第一周学习笔记(二)——Gradient内容请搜索靠谱客的其他文章。






![[Python]数据挖掘(1)、梯度下降求解逻辑回归——考核成绩分类ps:本博客内容根据唐宇迪的的机器学习经典算法 学习视频复制总结而来http://www.abcplus.com.cn/course/83/tasks逻辑回归](https://www.shuijiaxian.com/files_image/reation/bcimg14.png)

发表评论 取消回复