赴秦皇岛第三第四天集合

Sigmoid函数常被用作神经网络的阈值函数，将变量映射到0,1之间。
Sigmoid函数由下列公式定义

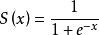
其对x的导数可以用自身表示:

摘要

几个主要的损失函数：MSE均方误差损失函数、SVM合页损失函数、Cross Entropy交叉熵损失函数、目标检测中常用的Smooth L1损失函数。其中还会涉及到梯度消失、梯度爆炸等问题：ESM均方误差+Sigmoid激活函数会导致学习缓慢；Smooth L1损失是为了解决梯度爆炸问题。仅供参考。

均方差损失函数
常用在最小二乘法中。它的思想是使得各个训练点到最优拟合线的距离最小（平方和最小）。以神经网络中激活函数的形式表达一下，定义如下：

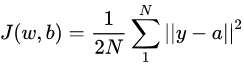
α=a=f(z)=f(w·x+b)：x是输出、w和b是网络的参数。f(·) 是激活函数。

2.2 ESM均方误差+Sigmoid激活函数：输出层神经元学习率缓慢

2.2.1 Sigmoid激活函数：

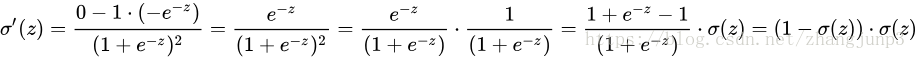
2.2.2 ESM均方误差+Sigmoid激活函数：输出层神经元学习率缓慢
我们以一个神经元，ESM均方误差损失 J=frac{1}{2}(y-a)^{2} ，Sigmoid激活函数 a=sigma (z) (其中 z=wx+b )为例，计算一下最后一层的反向传播过程，可得：

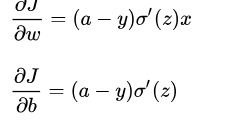
当神经元输出接近1时候，Sigmoid的导数 [公式] 变很小，这样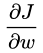 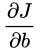很小，这就导致了MSE均方误差+Sigmoid激活函数使得神经网络反向传播的起始位置也就是说输出层神经元学习率缓慢。
想要解决这个问题，需要引入接下来介绍的交叉熵损失函数。交叉熵损失+Sigmoid激活函数可以解决输出层神经元学习率缓慢的问题，但是不能解决隐藏层神经元学习率缓慢的问题。
具体推导如下
交叉熵损失(Cross Entropy，CE)

多用于分类的损失函数。

***1、***交叉熵损失定义：

交叉熵损失的计算分为两个部分。

**（1）**softmax多分类器：

交叉熵损失是基于softmax计算来的，softmax将网络最后输出z通过指数转变成概率形式。首先看一下softmax计算公式：

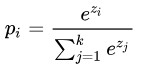
其中， 分子[公式] 是要计算的类别 [公式] 的网络输出的指数；分母是所有类别网络输出的指数和，共k个类别。这样就得到了类别i的输出概率 [公式] 。

→这里说点题外话，实际上，softmax是由逻辑斯的回归模型（用于二分类）推广得到的多项逻辑斯蒂回归模型（用于多分类）。具体可以参考李航大神的《统计学方法》第六章，这里给一个大致的过程。

（2）交叉熵损失：

公式定义如下： [公式]

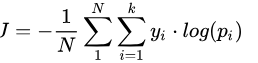
其中， [公式] 是类别 [公式] 的真实标签；[公式]是上面softmax计算出的类别 [公式] 的概率值；k是类别数，N是样本总数。

→这里看一个计算交叉熵损失的小例子：

假设共有三个类别cat、dog、bird，那么一张cat的图片标签应该为 [公式] 。并且训练过程中，这张cat的图片经过网络后得到三个类别网络的输出分别为3、1、-3。那么经过softmax可以得到对应的概率值，
3、交叉熵损失+Sigmoid激活函数：

（1）推导：

接着上一部分留下的问题，我们仍然以Sigmoid激活函数 [公式] (其中 [公式] )为例。这次我们引入交叉熵损失，并以二分类为例，那么s损失函数公式为：

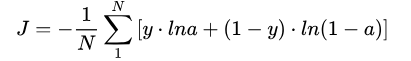
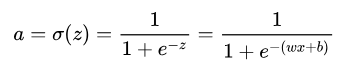
那么可以计算一下最后一层的反向传播过程，可得

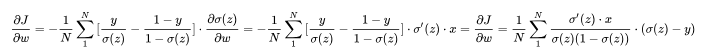
根据之前的推导已知
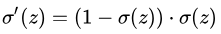[公式] ，那么上式可以化简为：


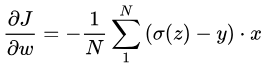
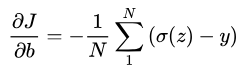
可以看到sigmoid的导数被约掉，这样最后一层的梯度中就没有[公式]。然而这只是输出层的推导，如果变成隐藏层的梯度sigmoid的导数不会被约掉，仍然存在[公式]。所以交叉熵损失+Sigmoid激活函数可以解决输出层神经元学习率缓慢的问题，但是不能解决隐藏层神经元学习率缓慢的问题。

（2）小结梯度消失问题：

其实损失函数包含两个部分：①计算方法（均方差、交叉熵等）②激活函数。

而之前我们遇到的是均方差损失+sigmoid激活函数造成了输出层神经元学习率缓慢，其实我们破坏任意一个条件都有可能解决这个问题：

①均方误差损失→交叉熵损失；

②sigmoid函数→不会造成梯度消失的函数，例如ReLU函数，不仅能解决输出层学习率缓慢，还能解决隐藏层学习率缓慢问题。

relu

结合生物神经元，采用任一非线性激活函数，都能使单层感知机具有求解线性不可分的能力。

以下摘自Physcal的博文ReLu(Rectified Linear Units)激活函数。

传统神经网络中最常用的两个激活函数，Sigmoid系（Logistic-Sigmoid、Tanh-Sigmoid）被视为神经网络的核心所在。

从数学上来看，非线性的Sigmoid函数对中央区的信号增益较大，对两侧区的信号增益小，在信号的特征空间映射上，有很好的效果。

从神经科学上来看，中央区酷似神经元的兴奋态，两侧区酷似神经元的抑制态，因而在神经网络学习方面，可以将重点特征推向中央区，将非重点特征推向两侧区。

2001年，神经科学家Dayan、Abott从生物学角度，模拟出了脑神经元接受信号更精确的激活模型。
这个模型对比Sigmoid系主要变化有三点：①单侧抑制 ②相对宽阔的兴奋边界 ③稀疏激活性（重点，可以看到红框里前端状态完全没有激活）

同年，Charles Dugas等人在做正数回归预测论文中偶然使用了Softplus函数，Softplus函数是Logistic-Sigmoid函数原函数。

按照论文的说法，一开始想要使用一个指数函数（天然正数）作为激活函数来回归，但是到后期梯度实在太大，难以训练，于是加了一个log来减缓上升趋势。

加了1是为了保证非负性。同年，Charles Dugas等人在NIPS会议论文中又调侃了一句，Softplus可以看作是强制非负校正函数

偶然的是，同是2001年，ML领域的Softplus/Rectifier激活函数与神经科学领域的提出脑神经元激活频率函数有神似的地方，这促成了新的激活函数的研究。

生物神经的稀疏激活性
在神经科学方面，除了新的激活频率函数之外，神经科学家还发现了神经元的稀疏激活性。

还是2001年，Attwell等人基于大脑能量消耗的观察学习上，推测神经元编码工作方式具有稀疏性和分布性。

2003年Lennie等人估测大脑同时被激活的神经元只有1~4%，进一步表明神经元工作的稀疏性。

从信号方面来看，即神经元同时只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽了，这样可以提高学习的精度，更好更快地提取稀疏特征。

从这个角度来看，在经验规则的初始化W之后，传统的Sigmoid系函数同时近乎有一半的神经元被激活，这不符合神经科学的研究，而且会给深度网络训练带来巨大问题。

Softplus照顾到了新模型的前两点，却没有稀疏激活性。因而，校正函数

人类中枢神经系统中约含1000亿个神经元；人眼有约1.2亿个视杆细胞，600万~700万的视锥细胞 。

几乎所有的神经元都是相互联系在一起，组成一个复杂的网络。

如果没有激活机制，信号的传递和网络训练将消耗巨大。ReLU激活函数使得神经元低于阈值时处于沉默状态。

ReLU相对于Sigmoid一方面大大降低运算（生物运算也有成本）；另一方面在输入信号较强时，仍然能够保留信号之间的差别。

3. ReLu的反向传播
   以下为《Notes on Convolutional Neural Networks》中的输出层反向传播公式。

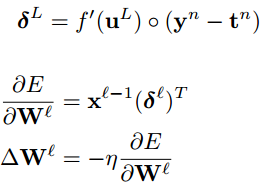
最后

以上就是疯狂诺言为你收集整理的赴秦皇岛第三第四天集合的全部内容，希望文章能够帮你解决赴秦皇岛第三第四天集合所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。