day02-回归定义和应用

心得体会

李宏毅老师的讲课幽默风趣，举了宝可梦的例子帮助理解，带入其中来解决实际问题。学到了很多之前没注意到的知识点，例如在做正则化操作时，不需要考虑bias的影响（bias的调整只是将目标函数的图像上下移动，不影响平滑度）。学习了回归问题的模型，首先进行模型假设，然后模型评估，选出优秀模型，最后进行模型优化。解决了如何避免陷入鞍点梯度下降如何跳过局部最优等问题。

在这里感谢datawhale开源社区的小伙伴们给予的学习帮助，今后的学习也要一样加油呀

提示：以下是本篇文章正文内容

模型步骤

• step1：模型假设，选择模型框架（线性模型）
• step2：模型评估，如何判断众多模型的好坏（损失函数）
• step3：模型优化，如何筛选最优的模型（梯度下降）

一、模型假设 - 线性模型

分清单个特征与多个特征
在实际应用中找到合适的输入特征

二、模型评估 - 损失函数

• 收集和查看训练数据
• 损失函数（Loss function） 来衡量模型的好坏

将 $w$, $b$ 在二维坐标图中展示

• 图中每一个点代表着一个模型对应的 $w$ 和 $b$
• 颜色越深代表模型更优

三、最佳模型 - 梯度下降

单个模型参数$w$
从最简单的只有一个参数$w$入手，定义$w^{\ast }=arg\underset{x}{\min }L(w)$

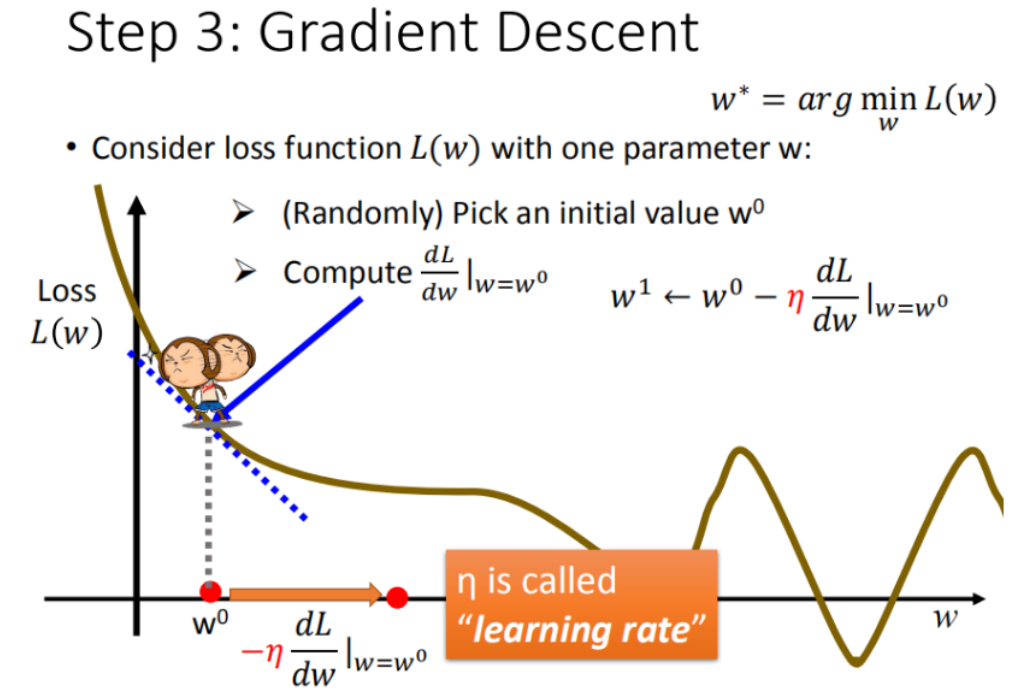
首先在这里引入一个概念 学习率 ：移动的步长，如图中 $\eta$

• 步骤1：随机选取一个 $w^0$
• 步骤2：计算微分，也就是当前的斜率，根据斜率来判定移动的方向
  • 小于0向右移动（增加$w$）
  • 大于0向左移动（减少$w$）
• 步骤3：根据学习率移动
• 重复步骤2和步骤3，直到找到最低点

2个模型参数 $w$ 和 $b$
通过梯度下降gradient descent不断更新损失函数的结果，公式如下：

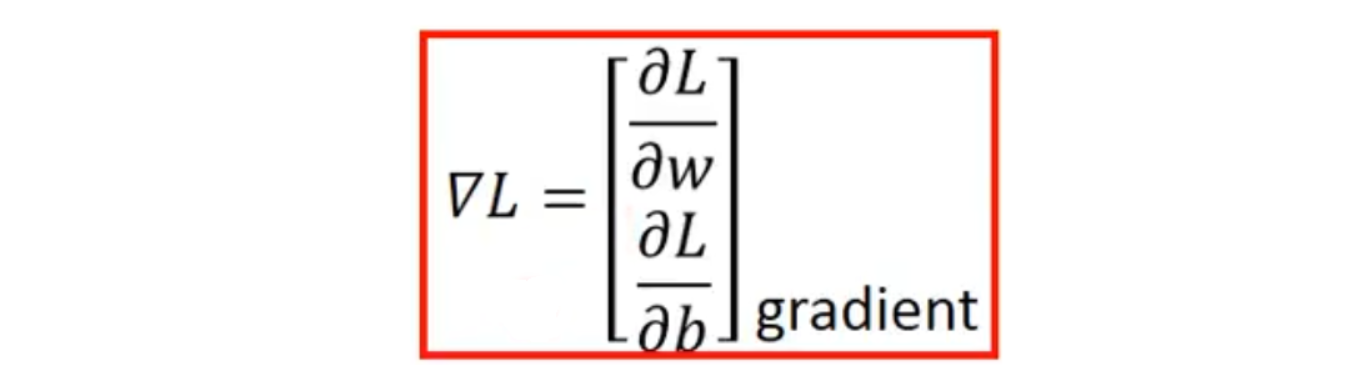
如何验证训练好的模型的好坏：使用训练集和测试集的平均误差来验证模型的好坏
在模型上，我们还可以进一部优化，选择更复杂的模型，使用更高次方的模型，可能会出现过拟合的问题。在训练集上面表现更为优秀的模型，在测试集上效果反而变差了

四、模型优化

• Step1优化：2个input的四个线性模型是合并到一个线性模型中
  通过对 Pokemons种类 判断，将 4个线性模型 合并到一个线性模型中

• Step2优化：如果希望模型更强大表现更好（更多参数，更多input）
  加入更多的特征，但数据量相对较少，故发生过拟合

• Step3优化：加入正则化
  更多特征，但是权重 $w$ 可能会使某些特征权值过高，仍旧导致overfitting，所以加入正则化
  权重 $w$ 越小，随着相同的$x$的变化，$y$的变化会更小，意味着function更加平滑。

回归演示

现在假设有10个x_data和y_data，x和y之间的关系是y_data=b+w*x_data。b，w都是参数，是需要学习出来的。现在我们来练习用梯度下降找到b和w。这里给出b和w特制化两种learning rate的代码：

# linear regression
b = -120
w = -4
lr = 1
iteration = 100000

b_history = [b]
w_history = [w]

lr_b=0
lr_w=0
import time
start = time.time()
for i in range(iteration):
    b_grad=0.0
    w_grad=0.0
    for n in range(len(x_data)):
        b_grad=b_grad-2.0*(y_data[n]-n-w*x_data[n])*1.0
        w_grad= w_grad-2.0*(y_data[n]-n-w*x_data[n])*x_data[n]
    
    lr_b=lr_b+b_grad**2
    lr_w=lr_w+w_grad**2
    # update param
    b -= lr/np.sqrt(lr_b) * b_grad
    w -= lr /np.sqrt(lr_w) * w_grad

    b_history.append(b)
    w_history.append(w)

问题补充与解决

如何避免陷入鞍点（局部最小）？

（1）以多组不同参数值初始化多个神经网络，去其中误差最小的作为结果

（2）使用“模拟退火”技术

模拟退火在每一步都以一定的概率接受比当前解更差的结果，从而有助于跳出局部最小值。在每次迭代过程中，接受’“次优解”的概率要随着时间的推移而逐渐降低，从而保证算法稳定。

（3）使用随机梯度下降

每次随机选取一个样本进行梯度下降，在梯度下降时加入了随机因素。即便陷入了局部最小点，它计算出的梯度可能仍不为零，这样就有机会跳出局部最小继续搜索。

如何解决梯度下降法的局部最优问题？
梯度下降本质上是一个贪心算法，容易陷入局部最优。通过梯度下降算法迭代得到的最优解（局部极小值）位置与待优化参数的初始值密切相关。此时解决该问题的一个简单办法是：在计算梯度时加入随机的因素，于是即便其陷入到局部的极小值点，他计算的梯度仍可能不为0，这样就有可能跳出局部的极小值而继续进行搜索。

梯度下降如何跳过局部最优（其他的方法）
下面列出了一些深度学习的优化方法（转载自一篇知乎大佬的文章）：

• SGD就是每一次迭代计算mini-batch的梯度，然后对参数进行更新。缺点：选择合适的learning rate比较困难且容易收敛到局部最优
• momentum是模拟物理里动量的概念，积累之前的动量来替代真正的梯度。
• nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度。
• Adagrad是对学习率进行了一个约束。依赖于人工设置一个全局学习率
  [公式]设置过大的话，会使regularizer过于敏感，对梯度的调节太大
  中后期，分母上梯度平方的累加将会越来越大，使得训练提前结束
• Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

参考资料：
深度学习最全优化方法总结比较：https://zhuanlan.zhihu.com/p/22252270
机器学习视频：https://www.bilibili.com/video/BV1Ht411g7Ef

最后

以上就是美满小兔子为你收集整理的day02-回归定义和应用的全部内容，希望文章能够帮你解决day02-回归定义和应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。