About Confidence Intervals

56 阅读 0 评论 37 点赞

我是靠谱客的博主默默西牛，最近开发中收集的这篇文章主要介绍About Confidence Intervals，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Much of machine learning involves estimating the performance of a machine learning algorithm on unseen data.

Confidence intervals are a way of quantifying the uncertainty of an estimate.

That a confidence interval is a bounds on an estimate of a population parameter.
That the confidence interval for the estimated skill of a classification method can be calculated directly.
That the confidence interval for any arbitrary population statistic can be estimated in a distribution-free way using the bootstrap.

1.1 Tutorial Overview

1. What is a Confidence Interval?

2. Interval for classfication Accuracy

3.Nonparametric Confidence Interval

1.2 What is a Confidence Interval?

A confidence interval is a bounds on the estimate of a population variable. It is an interval statistic used to quantify the uncertainty on an estimate.

A confidence interval is used to contain an unknown characteristic of the population or process. The quantity of interest might be a population property or “parameter”, such as the mean or standard deviation of the population or process.

A confidence interval is different from a tolerance interval that describes the bounds of data sampled from the distribution. It is also different from a prediction interval that describes the bounds on a single observation. Instead, the confidence interval provides bounds on a population parameter, such as a mean, standard deviation, or similar. In applied machine learning, we may wish to use confidence intervals in the presentation of the skill of a predictive model.

The value of a confidence interval is its ability to quantify the uncertainty of the estimate. It provides both a lower and upper bound and a likelihood. Taken as a radius measure alone, the confidence interval is often referred to as the margin of error and may be used to graphically depict the uncertainty of an estimate on graphs through the use of error bars. Often, the larger the sample from which the estimate was drawn, the more precise the estimate and the smaller (better) the confidence interval.

Smaller Confidence Interval: A more precise estimate.
Larger Confidence Interval: A less precise estimate.

1.3 Interval for Classification Accuracy

Classification problems are those where a label or class outcome variable is predicted given some input data. It is common to use classification accuracy or classification error (the inverse of accuracy) to describe the skill of a classification predictive model. For example, a model that makes correct predictions of the class outcome variable 75% of the time has a classification accuracy of 75%, calculated as:

This accuracy can be calculated based on a hold-out dataset not seen by the model during training, such as a validation or test dataset. Classification accuracy or classification error is a proportion or a ratio. It describes the proportion of correct or incorrect predictions made by the model. Each prediction is a binary decision that could be correct or incorrect.

We can use the assumption of a Gaussian distribution of the proportion (i.e. the classification accuracy or error) to easily calculate the confidence interval. In the case of classification error, the radius of the interval can be calculated as:

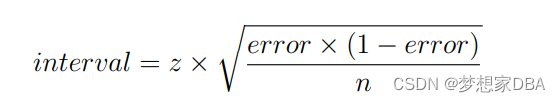
In the case of classification accuracy, the radius of the interval can be calculated as:

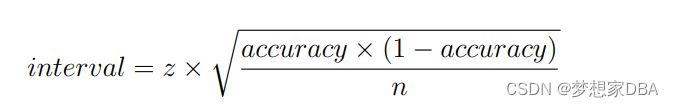
Consider a model with an error of 20%, or 0.2 (error = 0.2), on a validation dataset with 50 examples (n = 50). We can calculate the 95% confidence interval (z = 1.96) as follows:

# binomial confidence interval
from math import sqrt
# calculate the interval
interval = 1.96 * sqrt((0.2 * (1-0.2)) / 50)
print('%.3f'% interval)

Running the example, we see the calculated radius of the confidence interval calculated and printed.

We can then make claims such as:

The classification error of the model is 20% +/- 11%
The true classification error of the model is likely between 9% and 31%.

We can see the impact that the sample size has on the precision of the estimate in terms of the radius of the confidence interval.

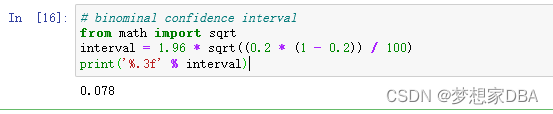
# binominal confidence interval
from math import sqrt
interval = 1.96 * sqrt((0.2 * (1 - 0.2)) / 100)
print('%.3f' % interval)

Running the example shows that the confidence interval drops to about 7%, increasing the precision of the estimate of the models skill.

The proportion confint() Statsmodels function an implementation of the binomial proportion confidence interval. By default, it makes the Gaussian assumption for the Binomial distribution, although other more sophisticated variations on the calculation are supported. The function takes the count of successes (or failures), the total number of trials, and the significance level as arguments and returns the lower and upper bound of the confidence interval. The example below demonstrates this function in a hypothetical case where a model made 88 correct predictions out of a dataset with 100 instances and we are interested in the 95% confidence interval (provided to the function as a significance of 0.05).

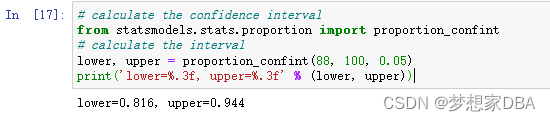
# calculate the confidence interval
from statsmodels.stats.proportion import proportion_confint
# calculate the interval
lower, upper = proportion_confint(88, 100, 0.05)
print('lower=%.3f, upper=%.3f' % (lower, upper))

Running the example prints the lower and upper bounds on the model’s classification accuracy.

1.4 Nonparametric Confidence Interval

Often we do not know the distribution for a chosen performance measure. Alternately, we may not know the analytical way to calculate a confidence interval for a skill score.

In these cases, the bootstrap resampling method can be used as a nonparametric method for calculating confidence intervals, nominally called bootstrap confidence intervals. The bootstrap is a simulated Monte Carlo method where samples are drawn from a fixed finite dataset with replacement and a parameter is estimated on each sample. This procedure leads to a robust estimate of the true population parameter via sampling. The bootstrap method was covered in detail in Chapter 17. We can demonstrate this with the following pseudocode.

statistics = []
for i in bootstraps:
sample = select_sample_with_replacement(data)
stat = calculate_statistic(sample)
statistics.append(stat)

The complete example is listed below:

# bootstrap confidence intervals
from numpy.random import seed
from numpy.random import rand
from numpy.random import randint
from numpy import mean
from numpy import median
from numpy import percentile
# seed the random number generation
seed(1)
# generate dataset
dataset = 0.5 + rand(1000) * 0.5
# bootstrap
scores = list()
for i in range(100):
    # bootstrap sample
    indices = randint(0, 1000, 1000)
    sample = dataset[indices]
    # calculate and store statistic
    statistic = mean(sample)
    scores.append(statistic)
print('50th percentile (median) = %.3f' % median(scores))
# calculate 95% confidence intervals (100 - alpha)
alpha = 5.0
# calculate lower percentile (2.5)
lower_p = alpha / 2.0
# retrieve observation at lower percentile
lower = max(0.0, percentile(scores,lower_p))
print('%.1fth percentile = %.3f' % (lower_p,lower))
#calculate upper percentile
upper_p = (100 - alpha) + (alpha / 2.0)
# retrieve observation at upper percentile
upper = min(1.0, percentile(scores, upper_p))
print('%.1fth percentile = %.3f' % (upper_p,upper))

Running the example summarizes the distribution of bootstrap sample statistics including the 2.5th, 50th (median) and 97.5th percentile.