台阶-Nim游戏台阶-Nim游戏

50 阅读 0 评论 33 点赞

我是靠谱客的博主谦让音响，最近开发中收集的这篇文章主要介绍台阶-Nim游戏台阶-Nim游戏，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

台阶-Nim游戏

题目描述

在这里插入图片描述

核心思路

结论：如果先手时奇数台阶上的值的异或值不为0，则先手必胜，反之先手必输。即对于先手来说，它面临的局面必须是奇数台阶上的数的异或值结果不为0，即 $A_1+A_3+cdots A_{i}+...$ 结果不为0

证明：

对于先手来说，如果它面临的局面是奇数台阶异或非0，根据经典Nim游戏定理可知，先手一定可以从某个奇数台阶中拿走一些石子，然后使得奇数台阶异或为0，即先手总有一种方式使奇数台阶异或为0，于是先手留了奇数台阶异或为0的状态给后手，也就是说后手面临的局面是奇数台阶异或值为0。

于是轮到了后手：

如果后手移动偶数台阶上的石子，那么先手只需将后手刚移动过的石子继续移到下一个台阶，这样奇数台阶的石子相当于没变，那么奇数台阶异或值仍然不变，于是留给后手的又是奇数台阶异或为0的状态。

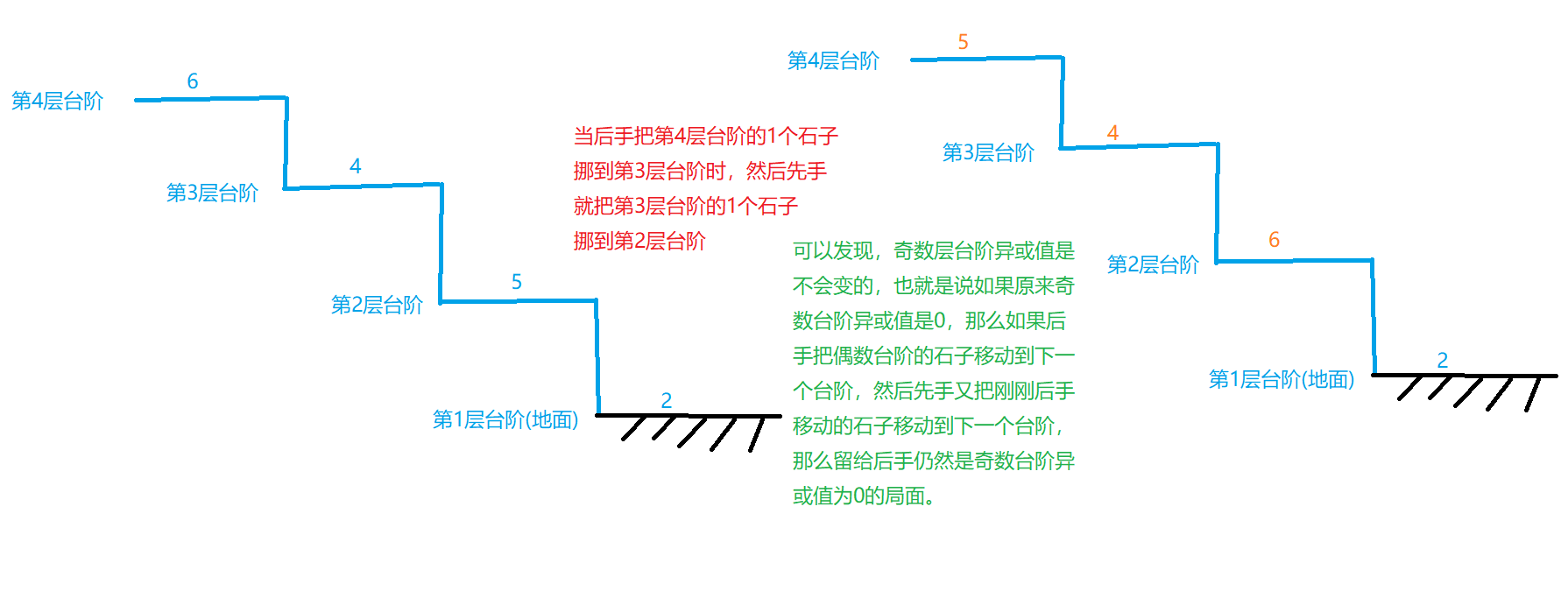
在这里插入图片描述

当后手移动奇数台阶上的石子时，由于后手它面临的是奇数台阶异或值为0的局面，由经典Nim定理可知，当后手随便拿出石子后，一定会得到奇数台阶异或值非0的局面。然后轮到了先手操作，此时先手面临奇数台阶异或值不为0的局面，由经典Nim定理可知，先手总能找出一种方案使奇数台阶异或为0。

因此，无论后手如何移动，先手总能通过操作把奇数台阶异或值为0的局面留给后手，一直循环这两种局面，先手面临的是奇数台阶异或值不为0的局面，后手面临的是奇数台阶异或值为0的局面。但是一定会有终止时刻，当奇数台阶全为0时，只留下偶数台阶上有石子。因为偶数台阶上的石子要想移动到地面，必然需要经过偶数次移动，又因为奇数台阶全0的情况是留给后手的，因此先手总是可以将石子移动到地面，当将最后一个（堆）石子移动到地面时，后手无法操作，即后手失败。也就是当先手把第一层台阶的石子挪到地面时，此时先手把奇数台阶异或值为0的局面抛给后手，但是此时由于没有石子可以移动了，因此后手无法操作，输了。

因此，这道题的做法就是：

求出奇数台阶异或值的结果res，判断res是否不为0，如果不为0，说明先手胜利，反之说明先手失败。

代码

#include<iostream>
typedef long long LL;
int n;
int main()
{
    scanf("%d",&n);
    LL res=0;   //记录奇数台阶异或值
    //从第1层台阶到第n层台阶
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        //处理奇数台阶的异或值
        if(i&1)
            res^=x;
    }
    //如果最终奇数台阶异或结果不为0,说明先手胜利
    if(res)
        puts("Yes");
    //如果最终奇数台阶异或结果为0,说明先手失败
    else
        puts("No");
    return 0;
}