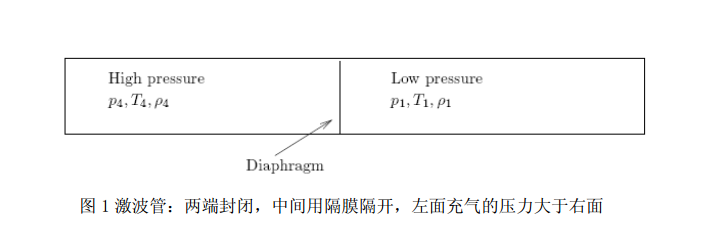
一、 简介: 一维激波管内流动是一个经典的流体问题,如图1,激波管左侧压强为p1,右侧压强为p2,中间用隔膜隔开,利用CFD技术模拟撤掉隔膜后管内的流动。
二、基础知识:
忽略粘性影响,运用欧拉方程:
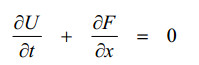
其中U和F均为矩阵形式。
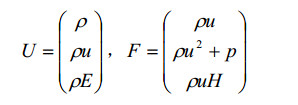
气体内能: e=CvT=RT/(γ-1);(γ=Cp/Cv为比热比)
气体 焓 : h=CpT=γRT/(γ-1);
气体总能: E=e+u²/2;
气体总焓: H=h+u²/2; H=E+p/ρ=E+RT;
采用CFD方法在计算机上模拟流体流动的本质是数值求解N-S方程,或忽略粘性的欧拉方程;而CFD的本质是流动控制方程的计算机程序。
三、CFD过程
① 准备工作:
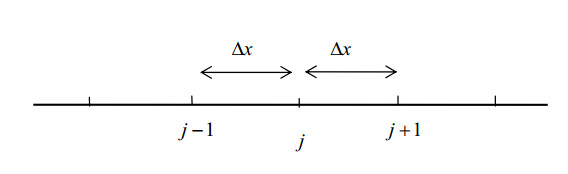
图 2 一维激波管网格划分
用差商代替偏微分形式:
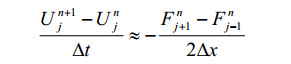
上述格式为FTCS格式(时间向前,空间差分的首字母缩写),若直接求解此方程会导致数值发散,所以需要改变形式。
所以,我们采用Lax格式求解:
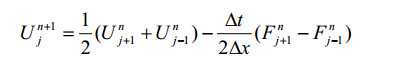
展开格式为:
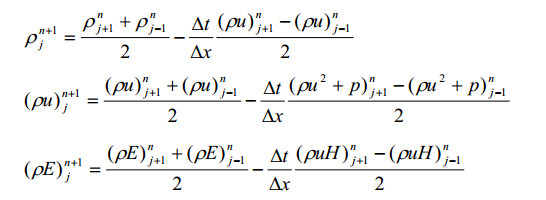
分析表明,Lax格式是条件稳定的,结果收敛的条件为:
CFL=|a|△t/△x<=1
②程序设计:
1.初始化各变量P,T,ρ,E,H,u,γ,∆x,R,计算音速a,CFL=0.98。P的前半段为P1=10bar,后半段为P2=1bar;T=300K;ρ由P1&P2以及R和T,分别计算出ρ1和ρ2;E1=e1+u²=e1=RT/γ-1,E2同理;H=E+p/ρ=E+RT;u=0;γ=1.4;∆x=0.1;R=287。
2.计算满足条件的∆t= CFL*∆x / max(a+u);
3.求解Lax格式的欧拉方程。
4.当达到所需物理时间时,停止计算,否则再次执行2、3步骤。
三、C++源码
//#include<iostream>
#include<fstream>#include<math.h>
#include<string>
#include<algorithm>
using namespace std;
double max(double *B, int n)//求数组B[n]中的最大值
{
double Max = *B;
for (int i = 0; i<n; ++i)
{
if (Max<*(B + i))
Max = B[i];
}
return Max;
}
int main()
{
const int nnod = 101;//节点数
ofstream out("out.txt");//将结果输出到该文件
double timeOut = 0.005;//要计算到该时间
double lendom = 10.0;//激波管长度
double dx = lendom / (nnod - 1);
double X[nnod];
X[0] = 0.0;
double Tini = 300.0;//温度
double PiniL = 10.0;//压力P1
double PiniR = 1.0;//压力P2
double uini = 0.0;//初始速度
double gamma = 1.4;//比热比
double R = 287.0;//理想气体常数J/kg/K
double CFL = 0.98;
double DiniL = 100000.0*PiniL / (R*Tini);//左边密度
double DiniR = 100000.0*PiniR / (R*Tini);//右边密度
double Eini = R*Tini / (gamma - 1.0);//初始内能
double Hini = Eini + R*Tini;//初始总焓
double aini = sqrt(gamma*R*Tini);//初始声速
double Den[nnod] = { 0 };
double Tem[nnod] = { 0 };
double Pre[nnod] = { 0 };
double Vel[nnod] = { 0 };
double M[nnod] = { 0 };
double Ene[nnod] = { 0 };
double Ent[nnod] = { 0 };
double a[nnod] = { 0 };
double a_v[nnod] = { 0 };
fill_n(Den, 101, 1.0);
fill_n(Tem, 101, 1.0);
fill_n(Pre, 101, 1.0);
fill_n(Vel, 101, 1.0);
fill_n(M, 101, 1.0);
fill_n(Ene, 101, 1.0);
fill_n(a, 101, 1.0);
double dt = CFL*dx / aini;
double U1[101] = { 0 };
double U2[101] = { 0 };
double U3[101] = { 0 };
fill_n(U1, 50, DiniL);
fill_n(U1+50, 51, DiniR);
fill_n(U2, 101, 0);
fill_n(U3, 50, DiniL*Eini);
fill_n(U3+50, 51, DiniR*Eini);
double Un[3][101] = { 0 };
double Un1[3][101] = { 0 };
memcpy(Un[0], U1, nnod*sizeof(double));
memcpy(Un[1], U2, nnod*sizeof(double));
memcpy(Un[2], U3, nnod*sizeof(double));
memcpy(Un1[0], Un[0], 101 * sizeof(double));
memcpy(Un1[1], Un[1], 101 * sizeof(double));
memcpy(Un1[2], Un[2], 101 * sizeof(double));
double F1[nnod] = { 0 };
double F2[nnod] = { 0 };
double F3[nnod] = { 0 };
double Fn[3][nnod];
fill_n(F2, 50, PiniL);
fill_n(F2+50, 51, PiniR);
memcpy(Fn[0], F1, nnod*sizeof(double));
memcpy(Fn[1], F2, nnod*sizeof(double));
memcpy(Fn[2], F3, nnod*sizeof(double));
double time = 0.0;
double DX(0);
for (int i(0); i<101; ++i)
{
X[i] = DX;
DX += dx;
}
while (time<timeOut)
{
time += dt;
for (int j(0); j<nnod; ++j)
{
if (j !=0 && j != (nnod-1))
{
Un1[0][j] = 0.5*(Un[0][j - 1] + Un[0][j + 1]);
Un1[1][j] = 0.5*(Un[1][j - 1] + Un[1][j + 1]);
Un1[2][j] = 0.5*(Un[2][j - 1] + Un[2][j + 1]);
Un1[0][j] = Un1[0][j]-dt/dx*(Fn[0][j + 1] - Fn[0][j - 1])*0.5;
Un1[1][j] = Un1[1][j]-dt/dx*(Fn[1][j + 1] - Fn[1][j - 1])*0.5;
Un1[2][j] = Un1[2][j]-dt/dx*(Fn[2][j + 1] - Fn[2][j - 1])*0.5;
}
}
for (int i(0); i<101; ++i)
{
Den[i] = Un1[0][i];
Vel[i] = Un1[1][i] / Den[i];
Ene[i] = Un1[2][i] / Den[i];
Tem[i] = (Ene[i] - 0.5*Vel[i] * Vel[i])*(gamma - 1.0) / R;
Pre[i] = R*Den[i] * Tem[i];
Ent[i] = Ene[i] + R*Tem[i];
a[i] = sqrt(gamma*R*Tem[i]);
M[i] = Vel[i] / a[i];
a_v[i] = a[i] + Vel[i];
}
dt = CFL*dx / (max(a_v, nnod));
//memcpy(Un1[0], Un[0], 3 * 101);
memcpy(Un[0], Un1[0], 101 * sizeof(double));
memcpy(Un[1], Un1[1], 101 * sizeof(double));
memcpy(Un[2], Un1[2], 101 * sizeof(double));
for (int j(0); j<101; ++j)
{
Fn[0][j] = Den[j] * Vel[j];
}
for (int j(0); j<101; ++j)
{
Fn[1][j] = Den[j] * Vel[j] * Vel[j]+Pre[j];
}
for (int j(0); j<101; ++j)
{
Fn[2][j] = Den[j] * Vel[j] * Ent[j];
}
}
out << "nnod"<< " "<<"dencity"<<" " << "pressure" << " " << "velocity" << " " << "Ma" << endl;
for (int i(0); i<101; ++i)
{
out << i << " " <<Den[i]<<" "<< Pre[i]<<" "<<Vel[i]<<" "<<M[i] << endl;
}
return 0;
}
最后
以上就是迷路往事最近收集整理的关于一维激波管内流动CFD实现(附C++源码)的全部内容,更多相关一维激波管内流动CFD实现(附C++源码)内容请搜索靠谱客的其他文章。








发表评论 取消回复