我是靠谱客的博主 炙热盼望,这篇文章主要介绍拟一维喷管流动的数值解——亚声速-超声速等熵喷管流动的非守恒型CFD解法(MacCormack方法)一、Matlab代码片二、计算结果展示,现在分享给大家,希望可以做个参考。
一、Matlab代码片
%亚声速-超声速等熵喷管流动 非守恒型麦考马克方法数值求解
clear; %清理内存变量
clc; %清理工作窗中的所有显示内容
r=1.4; %比热比
L=3; %喷管长度
i=31; %网格数目
C=0.5; %科朗数
x=linspace(0,L,i); %网格点横坐标
N=1401; %时间步
dx=L/(i-1); %空间步长
dt(1:N)=0; %时间步长
A=1+2.2*(x-1.5).*(x-1.5); %喷管面积
rho(N,i)=0; %流场密度赋值
T(N,i)=0; %流场温度赋值
V(N,i)=0; %流场速度赋值
%预分配内存
rhotav2(1:1400,1:30)=0; Vtav2(1:1400,1:30)=0;
%初始条件
rho(1,:)=1-0.3146*x; %流场密度初值
T(1,:)=1-0.2314*x; %流场温度初值
V(1,:)=(0.1+1.09*x).*(1-0.2314*x).^0.5; %流场速度初值
%按时间步长推进
for k=1:N-1
%计算预估步偏导数
rhot(1:i-1)=-V(k,1:i-1).*(rho(k,2:i)-rho(k,1:i-1))/dx-rho(k,1:i-1)...
.*(V(k,2:i)-V(k,1:i-1))/dx-rho(k,1:i-1).*V(k,1:i-1).*(log(A(2:i))-log(A(1:i-1)))/dx;
Vt(1:i-1)=-V(k,1:i-1).*(V(k,2:i)-V(k,1:i-1))/dx-1/r.*((T(k,2:i)...
-T(k,1:i-1))/dx+T(k,1:i-1)./rho(k,1:i-1).*(rho(k,2:i)-rho(k,1:i-1))/dx);
Tt(1:i-1)=-V(k,1:i-1).*(T(k,2:i)-T(k,1:i-1))/dx-(r-1).*T(k,1:i-1)...
.*((V(k,2:i)-V(k,1:i-1))/dx+V(k,1:i-1).*(log(A(2:i))-log(A(1:i-1)))/dx);
%确定最小时间步长
t=C*dx./(V(k,:)+sqrt(T(k,:)));
dt(k)=min(t);
%计算预估值
rho_(1:i-1)=rho(k,1:i-1)+rhot(1:i-1).*dt(k);
V_(1:i-1)=V(k,1:i-1)+Vt(1:i-1).*dt(k);
T_(1:i-1)=T(k,1:i-1)+Tt(1:i-1).*dt(k);
%校正偏导数
rhot_(2:i-1)=-V_(2:i-1).*(rho_(2:i-1)-rho_(1:i-2))/dx-rho_(2:i-1)...
.*(V_(2:i-1)-V_(1:i-2))/dx-rho_(2:i-1).*V_(2:i-1).*(log(A(2:i-1))-log(A(1:i-2)))/dx;
Vt_(2:i-1)=-V_(2:i-1).*(V_(2:i-1)-V_(1:i-2))/dx-1/r.*((T_(2:i-1)...
-T_(1:i-2))/dx+T_(2:i-1)./rho_(2:i-1).*(rho_(2:i-1)-rho_(1:i-2))/dx);
Tt_(2:i-1)=-V_(2:i-1).*(T_(2:i-1)-T_(1:i-2))/dx-(r-1).*T_(2:i-1)...
.*((V_(2:i-1)-V_(1:i-2))/dx+V_(2:i-1).*(log(A(2:i-1))-log(A(1:i-2)))/dx);
%时间导数平均值
rhotav(2:i-1)=0.5*(rhot(2:i-1)+rhot_(2:i-1)); rhotav2(k,2:i-1)=abs(rhotav(2:i-1));
Vtav(2:i-1)=0.5*(Vt(2:i-1)+Vt_(2:i-1));Vtav2(k,2:i-1)=abs(Vtav(2:i-1));
Ttav(2:i-1)=0.5*(Tt(2:i-1)+Tt_(2:i-1));
%流场变量校正值
rho(k+1,2:i-1)=rho(k,2:i-1)+rhotav(2:i-1)*dt(k);
V(k+1,2:i-1)=V(k,2:i-1)+Vtav(2:i-1)*dt(k);
T(k+1,2:i-1)=T(k,2:i-1)+Ttav(2:i-1)*dt(k);
%入流边界值
V(k+1,1)=2*V(k+1,2)-V(k+1,3);
rho(k+1,1)=1;
T(k+1,1)=1;
%出流边界值
rho(k+1,i)=2*rho(k+1,i-1)-rho(k+1,i-2);
V(k+1,i)=2*V(k+1,i-1)-V(k+1,i-2);
T(k+1,i)=2*T(k+1,i-1)-T(k+1,i-2);
%马赫数
Ma=V(1:k+1,1:i)./(sqrt(T(1:k+1,1:i)));
%流场压强
P=rho(1:k+1,1:i).*T(1:k+1,1:i);
end
%绘图 喷管喉道处密度、温度、压力和马赫数的变化
figure;
subplot(2,2,1),plot(1:1401,rho(1:1401,16),'b-');
ylabel('rho/rho_0'),xlabel('Timestep'); title('无量纲密度变化');
subplot(2,2,2),plot(1:1401,T(1:1401,16),'r-');
ylabel('T/T_0'),xlabel('Timestep');title('无量纲温度变化');
subplot(2,2,3),plot(1:1401,P(1:1401,16),'k-');
ylabel('P/P_0'),xlabel('Timestep');title('无量纲总压变化');
subplot(2,2,4),plot(1:1401,Ma(1:1401,16),'m-');
ylabel('Ma'),xlabel('Timestep');title('马赫数变化');
%绘图 喷管喉道处无量纲密度和速度时间导数的变化
figure;
plot(1:1400,rhotav2(1:1400,16),'k-');
ylabel('残差'),xlabel('Timestep');
title('喷管喉道处无量纲密度和速度时间导数的变化');
hold on;
plot(1:1400,Vtav2(1:1400,16),'k--');
%绘图 无量纲质量流量在六个不同时刻的瞬时分布
figure;
plot(x,rho(1,1:i).*V(1,1:i).*A(1:i),'k--');
hold on;
plot(x,rho(51,1:i).*V(51,1:i).*A(1:i),'r-');
hold on;
plot(x,rho(101,1:i).*V(101,1:i).*A(1:i),'b-');
hold on;
plot(x,rho(151,1:i).*V(151,1:i).*A(1:i),'g-');
hold on;
plot(x,rho(201,1:i).*V(201,1:i).*A(1:i),'y-');
hold on;
plot(x,rho(701,1:i).*V(701,1:i).*A(1:i),'m-');
title('不同时刻质量流量的变化');
ylabel('无量纲质量流量'),xlabel('无量纲轴向距离');
text(2.4,0.63,'700Deltat');
text(2.4,0.75,'150Deltat');
text(2.4,0.53,'200Deltat');
text(2.4,0.9,'50Deltat');
text(2.4,1.05,'100Deltat');
text(2.4,1.3,'0Deltat');
二、计算结果展示
1.喷管喉道处密度、温度、压力和马赫数的变化
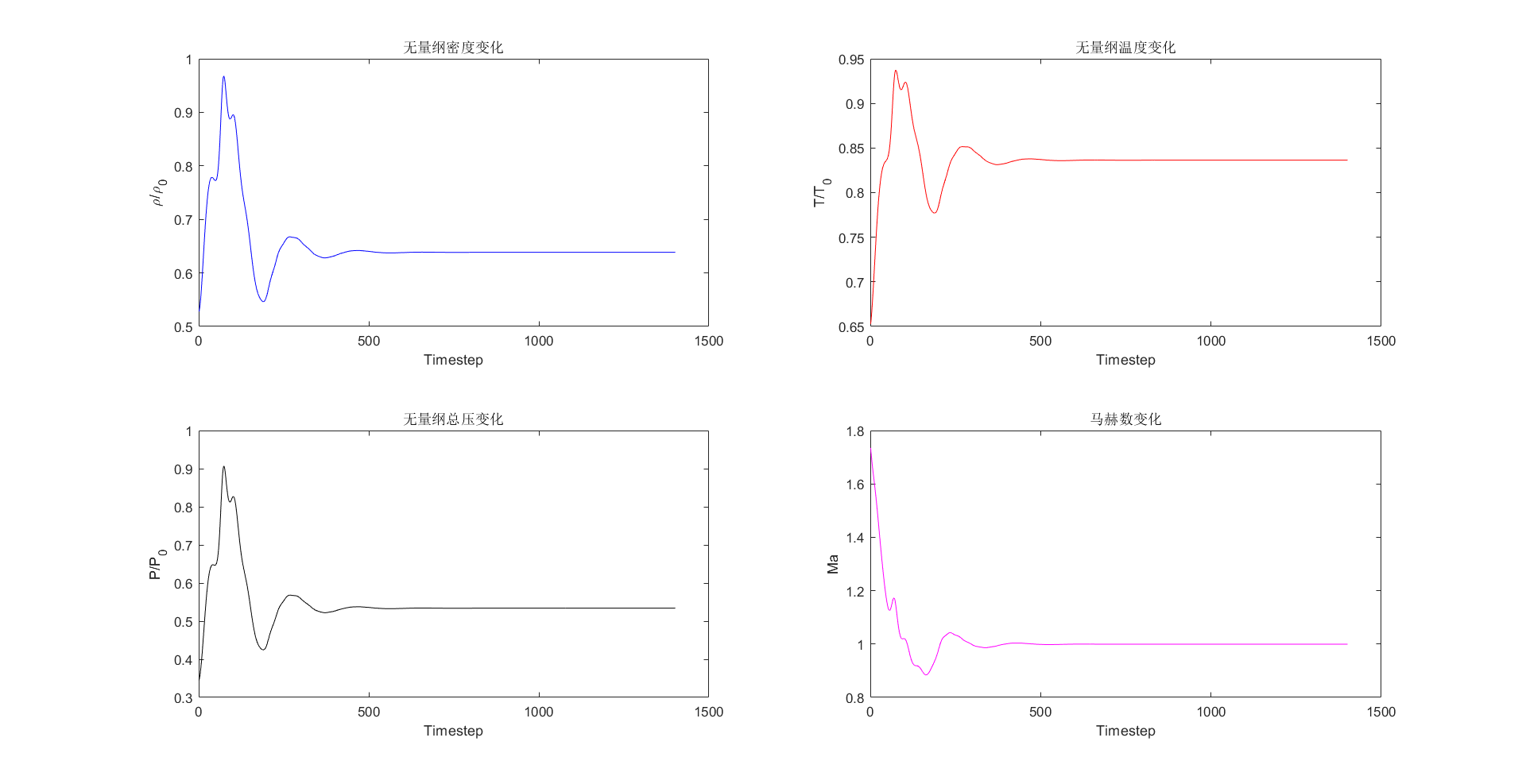
2.喷管喉道处无量纲密度和速度时间导数的变化
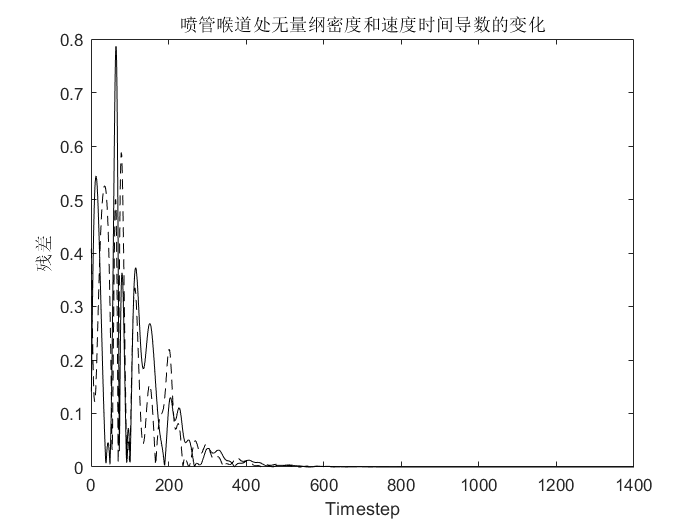
3.无量纲质量流量在六个不同时刻的瞬时分布
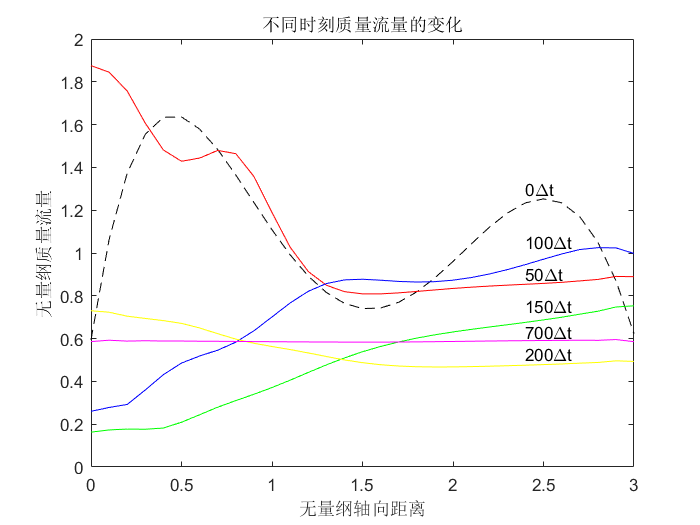
最后
以上就是炙热盼望最近收集整理的关于拟一维喷管流动的数值解——亚声速-超声速等熵喷管流动的非守恒型CFD解法(MacCormack方法)一、Matlab代码片二、计算结果展示的全部内容,更多相关拟一维喷管流动内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复