Reapted Games

之前学的基础模型几乎都是静态的（同时决策），除了斯坦伯格模型稍微带了点动态（领导者带领着跟随者）

重复博弈有以下特点：
1.和同一个人重复进行交互
2.动态的持续的
例子：
借给朋友钱，短期内可能是负收益，但是长期博弈的话，你借他，他以后可能也会帮你，也算是一个重复博弈（不包括那些…的人）

重复博弈，a （simultaneous-move）normal-form game(指普通的博弈) is played over and again by the same players.每玩一轮看到结果后，继续重复博弈，如持续的石头剪子布。（被重复的阶段称为重复博弈中的stage game）；

如果重复博弈不考虑重复，那么其实就还是一个normal-form博弈，也就是说只求解stage game的均衡就可以，但重复博弈中会考虑到历史数据，并且会更多的考虑到long time payoff（比如朋友请你帮忙，你会想着如果不帮记仇了怎么办巴拉巴拉，或者剪子石头布里一直用同样的策略，长期下来很有可能被对方猜到，然后被KO）’

（要有效利用历史信息）
（可能因为考虑长期利益而放弃短期利益）

策略1：grim trigger

grim trigger（冷酷出发，以牙还牙）
（参与人在开始时选择合作，在接下来的博弈中，如果对方合作则继续合作，而如果对方一旦背叛，则永远选择背叛，永不合作，只选择纳什均衡战略。）
（这是对grim trigger策略的一个解释，下边研究的模型更多的是假设知道玩家1用这个策略，另一个玩家会怎么办）

假如两个人进行重复博弈，stage game为囚徒困境，grim trigger就是说，如果第一次对方选了招，背叛了你，那你就以仇报仇，下次也会选背叛（但是如果考虑到长期利益，我背叛一次，对方也会背叛，那么两败俱伤，所以很可能不会选择背叛；另外从警察的角度来看，这样定惩罚可能以后犯人都不招了，所以警察可能会换一换惩罚值-这个就是题外话了）；

所以grim triger策略的第一种纳什均衡即为：双方两个人一直选合作（如果都有足够的耐心的话）；
另一种纳什均衡为全选背叛，因为任何一个人改变策略就会吃亏；（但是大概率考虑到自己利益会在一开始选择合作而不是背叛）

但是假如是有限重复博弈的话，且招带来的利益特别特别大，那么玩家2也可以在一定时刻改为招，即使后边两个人都是背叛，但他也因为那一局获得了很大的利益；如果是无限的话即使利益特别大，但是后边是无限的，也还是会考虑到从而不招

折扣因子discount

上一块有提到过，如果两个参与人都足够有耐心的话倾向于一直选择合作，但具体怎么衡量？
接下来引入一个折扣因子，可以理解为对每一局重复博弈有$1-\delta$的概率结束。

grim trigger

在有策略因子的情况下，假设玩家1采用grim trigger策略且初始态为合作，玩家2选择一直采用合作策略，假设收益为2，那么玩家2的期望收益为(用等比数列求和公式)：
$$u_2(h)=\sum _{t=0}^{\infty }{\delta }^{t}u(a_2^t)=\sum _{t=0}^{\infty }{\delta }^{t}2=\frac{2}{1-\delta }$$
如果玩家2选择背叛（也就是不采用冷酷触发策略），则玩家1由于grim trigger也会开始选择背叛从而达到另一种均衡，假设这是玩家2的收益序列为：3，1，1，1，1…
则期望收益为：
$$u_2(h)=\sum _{t=0}^{\infty }{\delta }^{t}u(a_2^t)=3+\delta +{\delta }^2+\dots =\frac{3-2\delta }{1-\delta }$$

令$\frac{2}{1-\delta }>\frac{3-2\delta }{1-\delta }$，即$\delta \ge \frac{1}{2}$时，玩家2选择合作带来的利益大，所以双方会保持一直合作的纳什均衡。

有限惩罚策略

在以上的grim trigger策略中，只要被背叛一次，那么玩家1接下来就会一直背叛，如果加一个条件，也就是有限惩罚，玩家1被背叛后选择k次背叛后无论对方选择什么会继续转向合作，用图表示的话就是这样：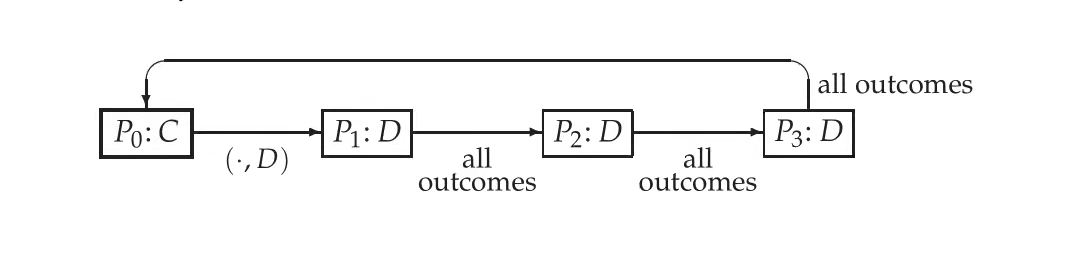
接下来继续引入折扣银子，分析假如玩家1选择有限惩罚策略，玩家2是个什么情况：
1.假如玩家2一开始就选择背叛，玩家1接着选择背叛，k个回合后，玩家1、2都开始（玩家2知道对手会开始合作，所以开始合作）继续选择合作，那么前k+1个回合的期望收益：
$$3+\delta +{\delta }^2+\dots +{\delta }^k=2+\frac{1-{\delta }^{k+1}}{1-\delta }$$
2.假如玩家12一直都是合作状态，则前k+1个回合期望收益为：
$$2+2\delta +2{\delta }^2+\dots +2{\delta }^k=\frac{2(1-{\delta }^{k+1})}{1-\delta }$$

令$\frac{2(1-{\delta }^{k+1})}{1-\delta }\ge 2+\frac{1-{\delta }^{k+1}}{1-\delta }$，得${\delta }^{k+1}-2\delta +1\le 0$，也就是说当$\delta$满足这个条件时，玩家2会选择一直合作；
下边讨论下这个条件何时有解：
1.k=1时，永远不成立，也就是说只惩罚1次太轻了，导致背叛的行为会发生；
2.k=2时，$\delta \ge 0.62$;
2.k=3时，$\delta \ge 0.55$;
当k增加时，$\delta$的下界会降低，降低意味着更重视长远利益。

以牙还牙策略

以牙还牙策略感觉比grim trigger放松了点，不是别人一背叛就自己也一直背叛了，而是会随着别人的策略调整，别人背叛也背叛，别人又合作了，自己就也合作了。

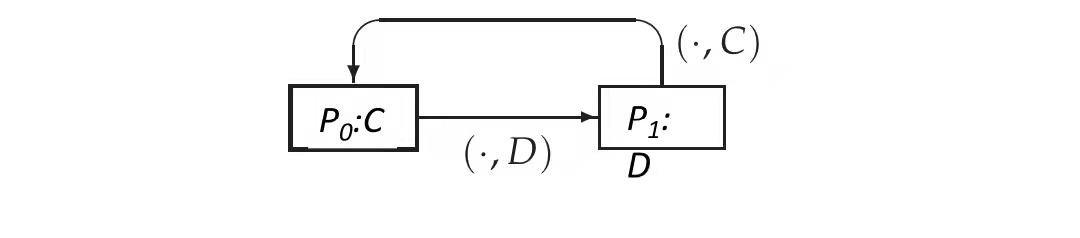
接下来继续引入折扣银子，分析假如玩家1选择以牙还牙策略（初始态选择合作），玩家2初始选择背叛是个什么情况：
1.玩家2一直选择背叛，计算得期望收益：
$$\frac{3-2\delta }{1-\delta }$$
2.玩家2选择初始背叛以及以牙还牙策略一会背叛一会合作的，也就是收益为3，0，3，0，3，0…,则期望收益为：
$$\frac{3}{(1-\delta )(1+\delta )}$$
3.玩家2初始不选择背叛以及以牙还牙策略，双方一直合作，之前已经算过了,期望收益为：
$$\frac{2}{1-\delta }$$
通过计算可以得到当$\delta \ge \frac{1}{2}$时，在玩家1初始选择合作的情况下玩家2一直选择合作是最好的策略，也就是双方都选择互相信任，以牙还牙策略。

总结or补充

1.精炼纳什均衡：只有当参与人的策略在每一个子博弈中都构成的纳什均衡叫做精炼纳什均衡，或者说组成精炼纳什均衡的策略必须在每一个子博弈中都是最优的，比如说一直选择背叛；
2.重复博弈理论对人们之间的合作提供了理性解释，比如囚徒困境，一次博弈的唯一纳什均衡为互相背叛，但是无限次的话，在一定条件下，二者可能就会选择合作；
3.如果stage game具有唯一纳什均衡，他被重复有限次，那么无论折现因子数值大小，它都将有唯一的子博弈完美均衡；如果被重复无穷多次，就不一定了;
4.无名氏定理（Folk Theorem）即在重复博弈中，只要博弈人具有足够的耐心（折现因子足够大），那么在满足博弈人个人理性约束的前提下，博弈人之间就总有多种可能达成合作均衡。存在无穷多对有限自动机策略，可以成为无限重复博弈的平衡点，并同时实现双方的合作。无名氏定理之所以得名，是由于重复博弈促进合作的思想，早就有很多人提出，以致无法追溯到其原创者，于是以“无名氏”命名之。

题目小结

1.采用grim trigger时，策略组合（strategy profile）：背叛，背叛是否是一个纳什均衡？
是（两个玩家从始至终一直都选择背叛，精炼纳什均衡），互为最优响应；
2.当玩家1采用grim策略，玩家2的最优响应是grim策略吗？
是；

最后

以上就是感动黑猫为你收集整理的重复博弈reapted gamesReapted Games总结or补充题目小结的全部内容，希望文章能够帮你解决重复博弈reapted gamesReapted Games总结or补充题目小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。