0. 引言

在强化学习问题中，探索和利用是一对矛盾： 探索 尝试不同的行为继而收集更多的信息，利用 则是做出当前信息下的最佳决定。

探索可能会牺牲一些短期利益，通过搜集更多信息而获得较为长期准确的利益估计；利用则侧重于对根据已掌握的信息而做到短期利益最大化。探索不能无止境地进行，否则就牺牲了太多的短期利益进而导致整体利益受损;同时也不能太看重短期利益而忽视一些未探索的可能会带来巨大利益的行为。因此如何平衡探索和利用是强化学习领域的一个课题。

根据探索过程中使用的数据结构，可以将 探索 分为: 依据状态行为空间的探索 (state-actionexploration)和 参数化搜索(parameter exploration)。前者 针对当前的每一个状态，以一定的算法 尝试 之前该状态下没有尝试过的 行为; 后者 直接针对参数化的策略函数，表现为 尝试 不同的 参数设置，进而得到具体的行为。

本章结合多臂赌博机实例一步步从理论角度推导得到一个有效的探索应该具备什么特征,随后介绍三类常用的探索方法:包括在前几章常用的 衰减的$ϵ$-贪婪探索 、 不确定优先探索 以及 利用信息价值进行探索 等。

1. 多臂赌博机

多臂赌博机游戏如下图所示。它由多个拉杆组成，每拉下一个拉杆，会获得一定的奖励（它不是一个恒定的值，而是一个概率分布），拉了一次后，状态序列结束。因此多臂赌博机中的一个完整状态序列就由一个行为和一个即时奖励构成，与状态无关。

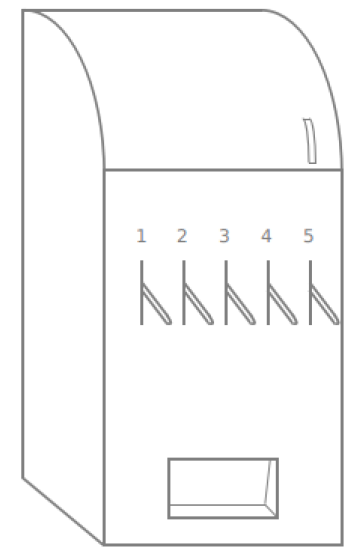
从上文的描述可以得出，多臂赌博机可以看成是由行为空间和奖励组成的元组$<A,R>$，假如一个多臂赌博机有m个拉杆，那么行为空间将由m个具体行为组成，每一个行为对应拉下某一个拉杆。个体采取行为$a$得到的即时奖励$r$服从一个个体未知的概率分布：

$$R^a(r)=P[r|a]$$

即：在$t$时刻，个体从行为空间$A$中选择一个行为$a_t\in A$,随后环境产生一个即时奖励$r_t\sim R^{a_t}$。

个体可以持续多次的与多臂赌博机进行交互，那么个体每次选择怎样的行为才能最大化来自多臂赌博机的累积奖励$({\sum }_{\tau =1}^t{r}_{\tau })$呢?

为了解决这个问题，首先定义 行为价值$Q(a)$ ：采取行为$a$获得的奖励期望（其实这就是之前的状态行为价值$Q$，只不过这个问题里没有状态而已），即:

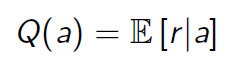
假设能够事先知道哪一个拉杆能够给出最大即时奖励，那可以每次只选择对应的那个拉杆。如果用$V^{\ast }$表示这个 最优价值，$a^{\ast }$表示能够带来最优价值的 行为，那么:

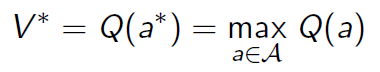
事实上不可能事先知道拉下哪个拉杆能带来最高奖励，因此采取动作$a_t$获得的奖励期望$Q(a_t)$都与最优价值$V^{\ast }$存在一定的差距，定义这个差距为 后悔值(regret):

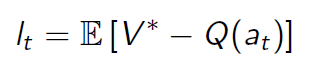
每执行一次拉杆行为都会产生一个后悔值$l_t$，随着拉杆行为的持续进行，将所有的后悔值加起来，形成一个 总后悔值:

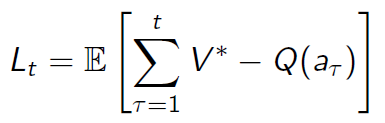
这样最大化累计奖励的问题就可以转化为 最小化总后悔值 了。之所以要进行这样的转换，是由于使用后悔值来分析问题较为简单、直观。

上式可以以另一种方式来重写。令$N_t(a)$为到$t$时刻时已执行行为$a$的次数，${\Delta }_a$为最优价值$V^{\ast }$与行为$a$对应的价值之间的差，那么总后悔值可以表示为;

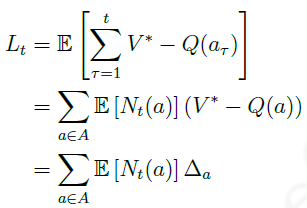
对于一个动作$a$的价值$Q(a)$，可以用蒙特卡罗算法得到的近似行为价值${\hat{Q}}_t(a)$来估计，即：

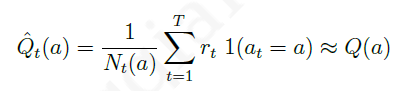
理论上$V^{\ast }$和$Q(a)$由环境动力学确定，因而都是静态的，随着 交互次数t的增多，可以认为蒙特卡罗评估得到的行为近似价值${\hat{Q}}_t(a)$ 越来越接近 真实的行为价值$Q(a)$。

下图是不同探索程度的贪婪策略 总后悔值 与 交互次数 的关系：

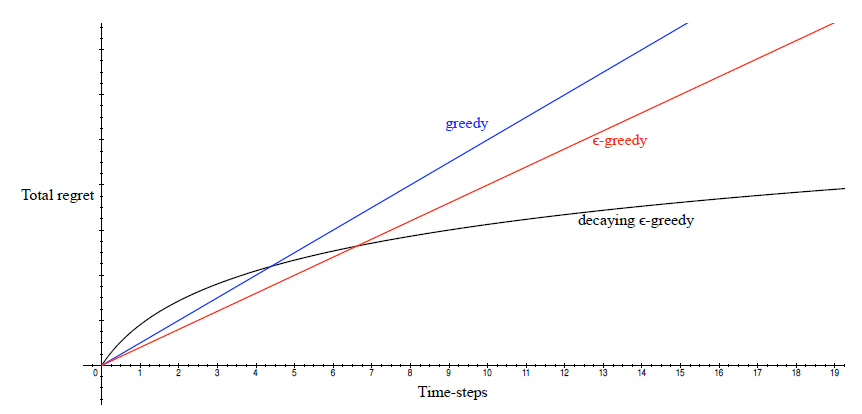
对于 完全贪婪 的探索方法，其总后悔值是线性的，这是因为该探索方法的行为选择可能会锁死在一个不是最佳的行为上;

对于 $ϵ$-贪婪 的探索方法，总后悔值也是呈线性增长，这是因为每一个时间步，该探索方法有一定的几率选择最优行为，但同样也有一个固定小的几率采取完全随机的行为，导致总后悔值也呈现与时间之间的线性关系。 softmax探索 方法与此类似。

总体来说，如果一个算法 永远存在探索 或者 从不探索，那么其总后悔值与时间的关系都是 线性增长 的。

能否找到一种探索方法，其对应的总后悔值与时间是 次线性增长，也就是随着时间的推移总后悔值的增加越来越少呢?答案是肯定的，上图中 衰减$ϵ$-贪婪方法 就是其中一种。下文将陆续介绍一些实际常用的探索方法。

2. 常用的探索方法

2.1 衰减$ϵ$-贪婪方法

衰减的$ϵ$-贪婪探索是在$ϵ$-贪婪探索上改进的，其核心思想是随着时间的推移，采用 随机行为的概率$ϵ$越来越小。理论上随时间改变的$ϵ-t$由下式确定︰

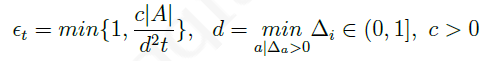
其中$d$是 次优行为 与 最优行为价值 之间的相对差距。

衰减的$ϵ$-贪婪探索能够使得总的后悔值呈现出与时间步长的 对数关系，但该方法需要事先知道每个行为的差距${\Delta }_a$，实际使用是无法按照该公式来准确确定${ϵ}_t$的，通常采用一些近似的衰减策略，这在之前几章已经有过介绍，比如单纯地就让$ϵ=1/k$，其中$k$是采样次数。

2.2 不确定行为优先探索

不确定行为优先探索 的基本思想是，当个体不清楚一个行为的价值时，个体有较高的几率选择该行为。

具体在实现时可以使用 乐观初始估计、 可信区间上限 以及 概率匹配 三种形式。

2.2.1 乐观初始估计

乐观初始估计给行为空间中的每一个行为在 初始 时赋予一个 足够高的价值，在选择行为时使用 完全贪婪 的探索方法，使用递增式的蒙特卡罗评估来更新这个价值:

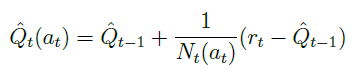
而上述中，足够高的价值通常是设为：

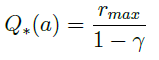
不难理解，乐观初始估计由于给每一个行为都赋予了一个足够高的价值，在实际交互时根据奖励计算得到的价值多数低于初始估计，一旦某行为由于尝试次数较多其价值降低时，贪婪的探索将选择那些行为价值较高的行为。

这种方法使得 每一个可能的行为都有机会被尝试，由于其本质仍然是完全贪婪的探索方法，因而 理论上 这仍是一个后悔值线性增长的探索方法，但 在实际应用中 乐观初始估计一般效果都不错。

2.2.2 置信区间上限

若存在几个拉杆在大部分的时候奖励相近，但是少数时候奖励忽高忽低，那么这时候应该选择哪个拉杆？

这时候可以通过比较两个拉杆 价值的差距($\Delta$) 以及描述其奖励分布相似程度的 KL散度($KL(R^a||R^{a^{\ast }}))$ 来判断总后悔值的下限。

一般来说，差距越大后悔值越大;奖励分布的相似程度越高，后悔值越低。针对多臂赌博机，存在一个 总后悔值下限，没有任何一个算法能做得比这个下限更好:

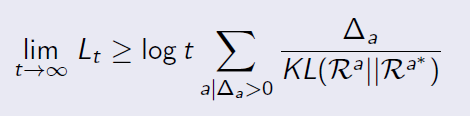
其中$t$是时间步长。

假设现在有一个三个拉杆的多臂赌博机，每一个拉杆给出的奖励服从一定的个体未知分布，先经过一定次数的对三个拉杆的尝试后，根据给出的奖励信息绘制得到如下图所示的奖励分布图：

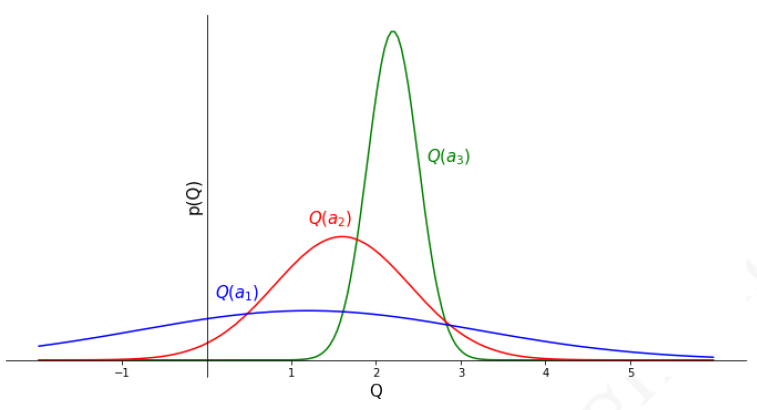
从上图可以看到，虽然$Q(a_3)$的均值最大，但是行为$a_1$存在一些远大于$Q(a_3)$的奖励，因此接下来应该优先地尝试行为$a_1$来弄清楚$a_1$的奖励分布，以减少奖励分布的方差。

从上面的分析可以看出，单纯用行为的奖励均值 作为行为价值的估计进而指导后续行为的选择会因为采样数量的原因而 不够准确，更加准确的办法 是估计行为价值 在一定可信度上的价值上限，比如可以设置一个行为价值95%的可信区间上限，将其作为指导后续行为的参考。如此一个行为的价值$Q(a)$将有较高的可信度不高于某一个值，即:

$$Q(a)\le {\hat{Q}}_t(a)+{\hat{U}}_t(a)$$

因此当一个行为的计数较少时，由均值估计的该行为的价值${\hat{Q}}_t(a)$将不可靠，对应的一定比例的价值可信区间上限$({\hat{Q}}_t(a)+{\hat{U}}_t(a))$将偏离均值较多；随着针对某一行为的奖励数据越来越多，该行为价值在相同可信区间的上限将接近均值，即：${\hat{U}}_t(a)\approx 0$。

因此，可以使用 置信区间上限(upper confidence bound,UCB) 作为行为价值的估计指导行为的选择。令:

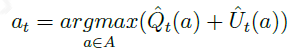
上式表示，每次采取行为时都用置信区间上限$({\hat{Q}}_t(a)+{\hat{U}}_t(a))$最大的行为$a_t$，而那些没采样或者采样次数较少的动作，其${\hat{U}}_t(a)$较大，从而会更优先被选择，这也是一种探索策略。

如果奖励的真实分布是明确已知的，那么置信区间上限可以较为容易地根据均值进行求解。例如对于高斯分布95%的置信区间上限是均值与约两倍标准差的和。

对于分布未知的置信区间上限的计算可以使用下式进行计算:

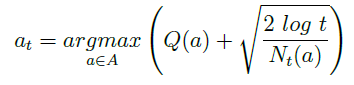
上式中$Q(a)$是根据交互经历得到的行为价值估计，$N_t(a)$是行为$a$被执行的次数，$t$是时间步长。这一公式的推导过程省略。

2.2.3 概率匹配

另一个基于不确定有限探索的方法是 概率匹配(probability matching)，它通过个体与环境的实际交互的 历史信息$h_t$ 估计行为空间中的 每一个行为 是 最优行为的概率，然后根据这个概率来采样后续行为:

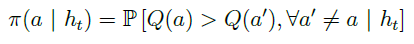
实际应用中常使用 汤姆森采样(Thompson sampling)，它是一种基于采样的概率匹配算法，具体行为$a$被选择的概率由下式决定︰

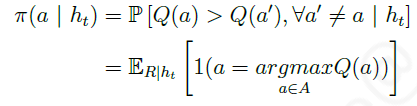
以具有$n$个拉杆的多臂赌博机为例，假设选择第$i$个拉杆的行为$a_i$一共有$m_i$次获得了历史最高奖励，那么使用汤姆森采样算法的个体将按照下式:

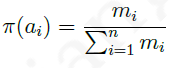
给出的策略来选择后续行为。汤姆森采样算法能够获得随时间 对数增长 的总后悔值。

2.3 基于信息价值的探索

探索之所以有价值是因为它会带来更多的信息，那么能否量化 被探索信息的价值 和 探索本身的开销 ，以此来决定是否有探索该信息的必要呢?这就涉及到信息本身的价值。

如果我们有充足的探索机会，比如还能够拉1000次拉杆，那么我们可以花费一定的次数（比如100次）去弄清楚那些不确定的拉杆的奖励分布，尽管可能会带来一些后悔值，但是后悔值是可控的，且一旦发现这个动作是能够获得很大的奖励时，能够大幅增加我们的最终奖励。如果我们本身就没有很多的探索机会，那么总是倾向于选择准确价值分布中，价值最大的动作。

为了能够确定信息本身的价值，可以设计一个 MDP，将信息作为MDP的状态构建对其价值的估计:

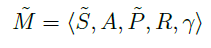
以有2个拉杆的多臂赌博机为例，一个信息状态对应于分别采取了行为$a_1$和$a_2$的次数，例如$S_0=<5,3>$可以表示一个信息状态，它意味着个体在这个状态时已经对行为$a_1$执行了5次，$a_2$执行了3次。随后个体又执行了一个行为$a_1$，那么状态转移至$S_1=<6,3>$。

由于基于信息状态空间的MDP其状态规模随着交互的增加而逐渐增加，因此使用表格式或者精确的求解这样的MDP是很困难的，通常使用近似价值和函数以及构建一个基于信息状态的模型并通过采样来近似求解。

虽然前文的这些探索方法都是基于与状态无关的多臂赌博机来讲述，但其均适用于存在不同状态转换条件下的 MDP问题，只需将状态$s$代入相应的公式即可。

参考文献：

1. David Silver强化学习视频.

2. 叶强《强化学习入门——从原理到实践》

最后

以上就是陶醉白羊为你收集整理的强化学习知识要点与编程实践（8）——探索与利用0. 引言1. 多臂赌博机2. 常用的探索方法的全部内容，希望文章能够帮你解决强化学习知识要点与编程实践（8）——探索与利用0. 引言1. 多臂赌博机2. 常用的探索方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。