衰减的$ϵ$-贪婪探索

衰减的$ϵ$-贪婪探索是在$ϵ$-贪婪探索上的改进，其核心思想是随着时间的推移，采用随机行为的概率$ϵ$越来越小。理论上随时间改变的$ϵ$-$t$由下式确定：
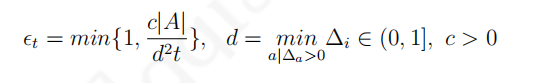其中$d$是次优行为与最优行为价值之间的相对差距。衰减的$ϵ$-贪婪探索能够使得总得后悔值呈现出与时间步长的对数关系，但该方法需要事先知道每个行为的差距${\Delta }_a$，实际使用是无法按照该公式来准确确定${ϵ}_t$的，通常采用一些近似的衰减策略。

不确定行为优先探索

不确定行为优先探索的基本思想是，当个体不清楚一个行为价值时，个体有较高的几率选择该行为。具体实现时可以使用乐观初始估计、可信区间上限以及概率匹配三种形式。

乐观初始估计

乐观初始估计给行为空间中的每一个行为在初始时赋予一个足够高的价值，在选择行为时使用完全贪婪的探索方法，使用递增式的蒙特卡罗评估来更新这个价值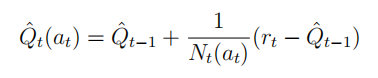：实际应用时，通常初始分配的行为价值为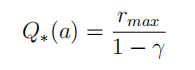：乐观初始估计由于给每一个行为都赋予了一个足够高的价值，在实际交互时根据奖励计算得到的价值多数低于初始估计，一旦某行为由于尝试次数较多其价值降低时，贪婪的探索将选择那些行为价值较高的行为，这种方法使得每一个可能的行为都有机会被尝试，由于其本质是完全贪婪的探索方法，因而理论上这仍是一个后悔值线性增长的探索方法，但在实际应用中乐观初始估计一般效果都还不错。

可信区间上限

以多臂赌博机为例，如果某一个拉杆一直给以较高的奖励而其他拉杆一直给出相对较低的奖励，那么行为的选择就容易多了。如果多个拉杆奖励的方差较大，忽高忽低，但这些拉杆实际给出的奖励多数情况下比较接近时，那么选择一个价值高的拉杆就不那么容易了，也就是说这些拉杆虽然给出的奖励接近，但实际上每一个拉杆奖励分布的均值却差距较大。 可以通过比较两个拉杆价值的差距($\Delta$)以及描述奖励分布相似程度的$KL$散度($KL(R^a||R^{a^{\ast }})$)来判断总后悔值的下限。一般来说，差距越大后悔值越大；奖励分布的相似程度越高，后悔值越低。针对多臂赌博机，存在一个总后悔值下限，没有任何一个算法能做得比这个下限更好：
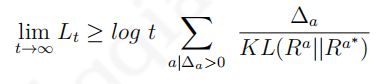假设现在有一个三个拉杆的多臂赌博机，每一个拉杆给出的奖励服从一定的个体未知分布，先经过一定次数的对三个拉杆的尝试后，根据给出的奖励信息绘制得到下图所示的奖励分布图。
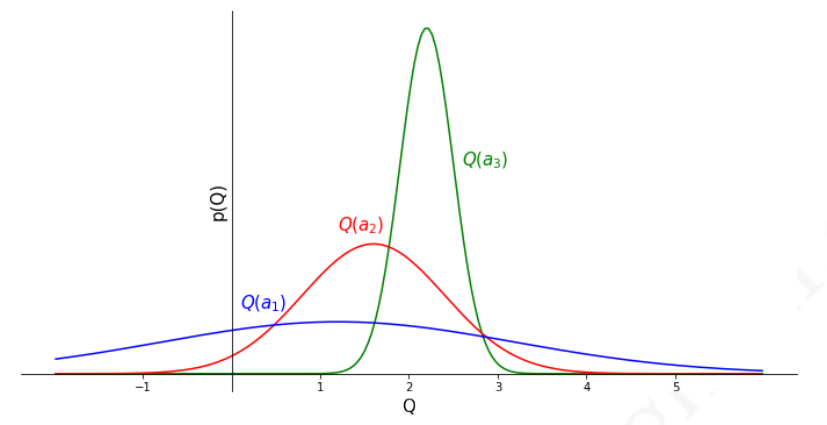从图中给出的三个拉杆奖励之间的相对关系，可以得出行为$a_3$的奖励分布较为集中，均值最高；行为$a_1$的奖励分布较为分散，均值最低；而行为$a_2$介于两者之间。虽然行为$a_1$对应的奖励均值最低，但其奖励分布较为分散，还有不少奖励超过了均值最高的行为$a_3$的平均均值，说明对行为$a_1$的价值估计较不准确，此时为了弄清楚行为$a_1$的奖励分布，应该优先尝试更多次行为$a_1$，以尽可能缩小其奖励分布的方差。
从上面的分析可以看出，单纯用行为的奖励均值作为行为价值的估计进而指导后续行为的选择会因为采样数量的原因而不够准确，更加准确的办法是估计行为价值在一定可信度上的价值上限，比如可以设置一个行为价值$95\%$的可信区间上限，将其作为指导后续行为的参考。如此一个行为的价值将有较高的可信度不高于某一个值：
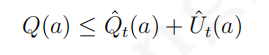因此当一个行为的计数较少时，由均值估计的该行为的价值将不可靠，对应的一定比例的价值可信区间上限将偏离均值较多；随着针对某一行为的奖励数据越来越多，该行为价值在相同可信区间的上限将接近均值。因此，可以使用置信区间上限($upperconfidencebound,UCB$)作为行为价值的估计指导行为的选择。令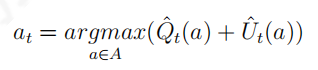：如果奖励的真实分布是明确已知的，那么置信区间上限可以较为容易地根据均值进行求解。例如对于高斯分布$95\%$的置信区间上限是均值与约两倍标准差的和。对于分布未知的置信区间上限的计算可以使用下式计算：
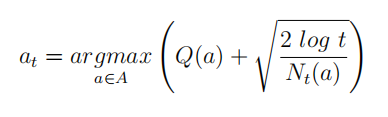式中$Q(a)$是根据交互经历得到的行为价值估计，$N_t(a)$是行为$a$被执行的次数，$t$是时间步长。公式的推导过程如下：
定理： 令$X_1,X_2,...,X_t$是值在区间$[0,1]$上独立同分布的采样数据，令$\overline{X_t}=\frac{1}{\tau }{\sum }_{\tau =1}^t{X}_{\tau }$是采样数据的平均值，那么下面的不等式成立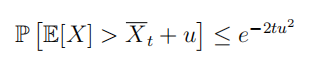：该不等式称为霍夫丁不等式。它给出了总体均值与采样均值之间的关系。根据该不等式可以得到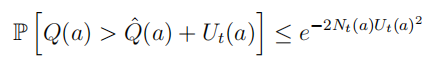：该不等式同样描述了一个置信区间上限，假定某行为的真实价值有$p$的概率超过设置的可信区间上限，即令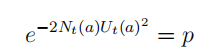：那么可以得到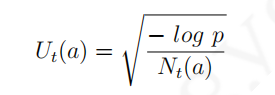：随着时间步长的增加，$p$值逐渐减少，假设令$p=t^{-4}$，上式则变为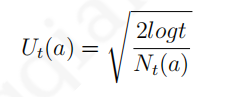：由此得证。
根据置信区间上限$UCB$算法原理设计的探索方法可以使得总后悔值随时间步长满足对数渐进关系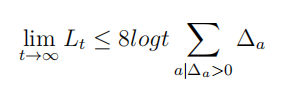：经验表明，$ϵ$-贪婪探索的参数如果调整得当可以有很好的表现，而$UCB$在没有掌握任何信息的前提上也可以表现很好。
如果多臂赌博机中的每一个拉杆奖励服从相互独立的高斯分布，即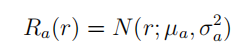：那么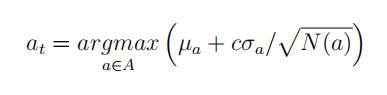：由于自然界许多现象都可以用高斯分布来近似描述，因此许多情况下可以使用上式来指导探索。

概率匹配

概率匹配通过个体与环境的实际交互的历史信息$h_t$估计行为空间中的每一个行为是最优行为的概率，然后根据这个概率来采样后续行为：
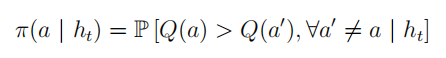实际应用中常使用汤姆森采样，它是一种基于采样的概率匹配算法，具体行为$a$被选择的概率由下式决定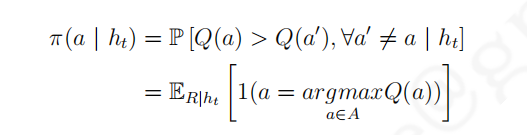：以具有$n$个拉杆的多臂赌博机为例，假设选择第$i$个拉杆的行为$a_i$一共有$m_i$次获得了历史最高奖励，那么使用汤姆森采样算法的个体将按照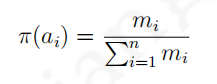：给出的策略来选择后续行为。汤姆森采样算法能够获得随时间对数增长的总后悔值。

基于信息价值的探索

为了能够确定信息本身的价值，可以设计一个$MDP$，将信息作为$MDP$的状态构建对其价值的估计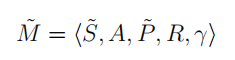：以有$2$个拉杆的多臂赌博机为例，一个信息状态对应于分别采取了行为$a_1$和$a_2$的次数，例如$S_0<5,3>$可以表示一个信息状态，它意味着个体在这个状态时已经对行为$a_1$执行了$5$次，$a_2$执行了$3$次。随后个体又执行了一个行为$a_1$，那么状态移至$S_1<6,3>$。
由于基于信息状态空间的$MDP$其状态规模随着交互的增加而逐渐增加，因此使用表格式或者精确的求解这样的$MDP$是很困难的，通常使用近似架子和函数以及构建一个基于信息状态的模型并通过采样来近似求解。
虽然前文的这些探索方法都是基于与状态无关的多臂赌博机讲述，但其均适用于存在不同状态转换条件下的$MDP$问题，只需将状态$s$代入相应的公式即可。

最后

以上就是俊秀酒窝为你收集整理的强化学习之探索与利用(二)衰减的 ϵ \epsilon ϵ-贪婪探索不确定行为优先探索基于信息价值的探索的全部内容，希望文章能够帮你解决强化学习之探索与利用(二)衰减的 ϵ \epsilon ϵ-贪婪探索不确定行为优先探索基于信息价值的探索所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。