【算法】完全二叉树的节点数计算

再讲完全二叉树节点数计算之前，我们先来看什么是完全二叉树

完全二叉树就是，树的高度差最多为1，且最后一层的节点都是紧凑靠左排列的。

满二叉树就是一种特殊的完全二叉树**，每层都是满的，除叶子结点外，每一层都有两个子节点**：

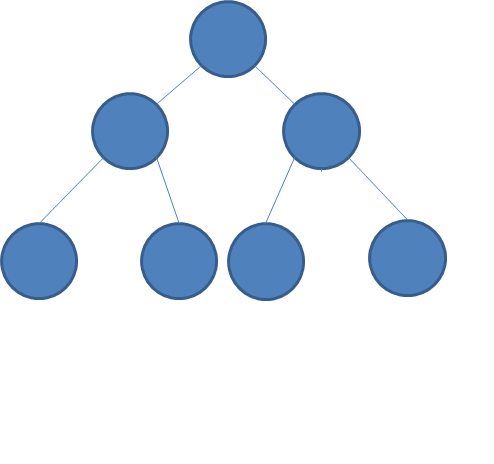
我们现在来看如何计算完全二叉树的节点个数呢？

如果是一个普通的二叉树，显然只要向下遍历一遍就行，时间复杂度为 O(N)

int countNodes(TreeNode* root)
{
	if(root == nullptr) 
		return 0 ;
	return 1 + countNodes(root->left) + countNodes(root->right);
}

那么如果是一个满二叉树，节点总数与高度呈指数关系，时间复杂度为O(logN)

int countNodes(TreeNode* root)
{
	int h = 0;
	while(root != nullptr)
	{
		root = root->left;
		h++;
	}
	return pow(2,h) - 1;
}

完全二叉树，比普通二叉树普通，但是又没有满二叉树那么特殊所以它分情况看用哪一种算法。

int coutNodes(TreeNode *root)
{
	TreeNode* l = root;
	TreeNode* r = root;
	int hleft = 0;
	int hright = 0;
	while(l != nullptr)
	{
		l = l->left;
		hleft++;
	}
	while(r != nullptr)
	{
		r = r->right;
		hright++;
	}
	//如果左右子树的高度相同，则是一颗满二叉树
	if(hleft == hright)
		return pow(2,hleft) - 1;
	
	else //按照普通二叉树的逻辑进行计算
		return 1 + countNodes(root->left) + countNodes(root->right);
}

最后

以上就是眯眯眼指甲油为你收集整理的【算法】完全二叉树的节点数计算的全部内容，希望文章能够帮你解决【算法】完全二叉树的节点数计算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。