C. 【UER #7】套路

反攻正在进行中，按照套路，跳蚤国将会很快获得最终的胜利。跳蚤国的情报局也没闲下来，他们正打算派遣一批“菲克蚤”前往跳晚国窃取有关三星 note7 的资料。

Fake Yang 是这批“菲克蚤”的教练，他教会他们各种 Fake 的技术，以便更好混入敌方内部。共  n n 只菲克蚤，由  1 1 到  n n 编号。Fake Yang 给每个菲克蚤都算了特征值  a1,…,an a1,…,an，两个菲克蚤的相似度定义成这两个菲克蚤的特征值的差的绝对值，即第  i i 只菲克蚤与第  j j 只菲克蚤的相似度为  ∣ai−aj∣ ∣ai−aj∣。

现在这批菲克蚤排成一列在 Fake Yang 面前，Fake Yang 需要在其中选出一些菲克蚤合成一个行动小队。按照套路，他会选取连续一整段的菲克蚤  al,al+1,…,ar al,al+1,…,ar。很显然，这个行动小队越大越好，但是按照套路，小队内的跳蚤最好都各不相同，假如有两只跳蚤长得很像的话很可能会引起跳晚们的怀疑。为此 Fake Yang 将小队的相似度定义为小队中的跳蚤两两之间的最小的相似度，用  s(l,r) s(l,r) 表示。

为保证安全，现在他想选取至少  k k 只跳蚤，且使得安全值最大。其中安全值定义如下：

但是，他并不知道最优解是什么，于是按照套路你需要帮助他求得这个值。

输入格式

按照套路，第一行三个正整数  n,m,k n,m,k。 k k 的意义如前所述， n n 表示跳蚤的只数。

接下来一行  n n 个整数，按照套路依次表示  n n 只跳蚤的特征值  a1,…,an a1,…,an，保证  1≤ai≤m 1≤ai≤m。

输出格式

按照套路，一行一个整数，表示答案。

样例一

input

10 10 2
1 4 2 6 1 9 6 8 10 3

output

8

explanation

一种方案是选取区间[5,6],相似度为8,那么答案为(6-5）×8=8

限制与约定

由于一些原因，本题我们需要按照套路使用捆绑测试。每个子任务有若干个测试点，分为  5 5 个子任务，你只有通过一个子任务的所有测试点才能按照套路得到这个子任务的分数。

【题解】

【分成两部分来搞，然而为什么？？？窝不知道，感性的理解下伐。ATP和zyf说：不分开搞怎么保证时间复杂度。。。（好伐，貌似好有道理诶！）】

【题解上说：】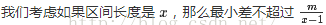

【PART 1】【考虑k<=S的情况，一部分近乎暴力，i枚举的是有多少个跳蚤包含在小组里，j枚举的是当前小组的起点，每次用小组的最后一个元素减去第一个元素并与当前小组的最小差比较、更新（因为i从2开始枚举，前面的数之间的差都已经算过）】

【PART 2】【这一段是固定右边界和最小差值，寻找左边界，i枚举右边界，j枚举最小差值j+1。每次用已固定的右边界的值上下浮动j,查找最大区间 】

#include<cstdio>
#include<cstring>
#include<algorithm>
#define S 500
using namespace std;
int a[200010],n,m,k,ans;
int r[200010],f[200010],l[200010];
inline int abss(int x)
{
	if(x>=0) return x;
	return -x;
}
int main()
{
	int i,j;
	scanf("%d%d%d",&n,&m,&k);
	for(i=1;i<=n;++i) scanf("%d",&a[i]);
	memset(f,127,sizeof(f));
	for(i=2;i<=S;++i)
	 for(j=1;j+i-1<=n;++j)
	  {
	  	int x=abss(a[i+j-1]-a[j]);
	  	f[j]=(f[j]<f[j+1]?f[j]:f[j+1]); 
		f[j]=(f[j]<x?f[j]:x);
		if(i>=k) ans=max(ans,f[j]*(i-1));
	  }
	//PART 1
    int N=(k>S?k:S);
	for(i=1;i<=n;++i)
	 {
	 	for(j=0;j<=S;++j)
	 	 {
	 	 	int x=(j==0?0:l[j-1]);
	 	 	l[j]=(l[j]>x?l[j]:x);
	 	 	if(a[i]-j>=1) l[j]=(l[j]<r[a[i]-j]?r[a[i]-j]:l[j]);
	 	 	if(a[i]+j<=m) l[j]=(l[j]<r[a[i]+j]?r[a[i]+j]:l[j]);
	 	 	if(i-l[j]>=N) ans=max(ans,(i-l[j]-1)*(j+1));
		  }
		r[a[i]]=i;//因为在超过N的区间大小里可能有重复元素，所以要每次尽量将最右端右移,这样可以使下一次枚举区间时满足条件的区间尽量大 
	  } 
	//PART 2 
	printf("%dn",ans);
	return 0;
}

最后

以上就是迷人毛衣为你收集整理的【UOJ 测试】C. 【#246 UER #7】套路（乱搞+枚举） C. 【UER #7】套路的全部内容，希望文章能够帮你解决【UOJ 测试】C. 【#246 UER #7】套路（乱搞+枚举） C. 【UER #7】套路所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。