LC-6255. 两个城市间路径的最小分数（BFS、DFS）【周赛322】6255. 两个城市间路径的最小分数

69 阅读 0 评论 46 点赞

我是靠谱客的博主唠叨信封，最近开发中收集的这篇文章主要介绍LC-6255. 两个城市间路径的最小分数（BFS、DFS）【周赛322】6255. 两个城市间路径的最小分数，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

6255. 两个城市间路径的最小分数

难度中等2

给你一个正整数 n ，表示总共有 n 个城市，城市从 1 到 n 编号。给你一个二维数组 roads ，其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条双向道路，道路距离为 distancei 。城市构成的图不一定是连通的。

两个城市之间一条路径的分数定义为这条路径中道路的最小距离。

城市 1 和城市 n 之间的所有路径的最小分数。

注意：

一条路径指的是两个城市之间的道路序列。
一条路径可以多次包含同一条道路，你也可以沿着路径多次到达城市 1 和城市 n 。
测试数据保证城市 1 和城市n 之间至少有一条路径。

示例 1：
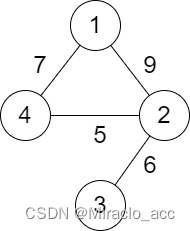
在这里插入图片描述

输入：n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出：5
解释：城市 1 到城市 4 的路径中，分数最小的一条为：1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。

示例 2：

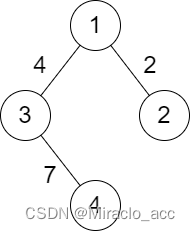
在这里插入图片描述

输入：n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出：2
解释：城市 1 到城市 4 分数最小的路径是：1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。

提示：

2 <= n <= 105
1 <= roads.length <= 105
roads[i].length == 3
1 <= ai, bi <= n
ai != bi
1 <= distancei <= 104
不会有重复的边。
城市 1 和城市 n 之间至少有一条路径。

BFS

取连通块中最小的边

class Solution {
    int ans = (int)1e9;
    List<int[]>[] g;
    public int minScore(int n, int[][] roads) {
        g = new ArrayList[n+1];
        Arrays.setAll(g, e -> new ArrayList<int[]>());
        for (var e : roads) {
            int u = e[0], v = e[1], cnt = e[2];
            g[u].add(new int[]{v, cnt});
            g[v].add(new int[]{u, cnt}); // 建图
        }
        Deque<Integer> dq = new ArrayDeque<>();
        boolean[] visited = new boolean[n+1];
        dq.addLast(1);
        visited[1] = true;
        while(!dq.isEmpty()){
            int size = dq.size();
            while(size-- > 0){
                int idx = dq.pollLast();
                List<int[]> list = g[idx];
                for(int[] edge : list){
                    int to = edge[0], val = edge[1];
                    ans = Math.min(ans,val);
                    if(!visited[to]){
                        visited[to] = true;
                        dq.addFirst(to);
                    }
                }
            }
        }
        
        return ans;
    }
    
    
}

DFS

class Solution {
    int ans = (int)1e9;
    boolean[] visited;
    public int minScore(int n, int[][] roads) {
        List<int[]>[] g = new ArrayList[n+1];
        Arrays.setAll(g, e -> new ArrayList<int[]>());
        for (var e : roads) {
            int u = e[0], v = e[1], cnt = e[2];
            g[u].add(new int[]{v, cnt});
            g[v].add(new int[]{u, cnt}); // 建图
        }
        
        visited = new boolean[n+1];
        dfs(1, g);
        return ans;
    }

    public void dfs(int idx, List<int[]>[] g){
        visited[idx] = true;
        List<int[]> list = g[idx];
        for(int[] arr : list){
            int to = arr[0], val = arr[1];
            ans = Math.min(ans,val);
            if(!visited[to]){
                dfs(to,g);
            }
        }
    }
}