动态规划详解数塔问题

112 阅读 0 评论 74 点赞

我是靠谱客的博主贤惠火龙果，最近开发中收集的这篇文章主要介绍动态规划详解数塔问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

下图是一个数塔，从顶部出发在每一个节点可以选择向左或者向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大. (f[i][j]表示数塔所在位置的数字)
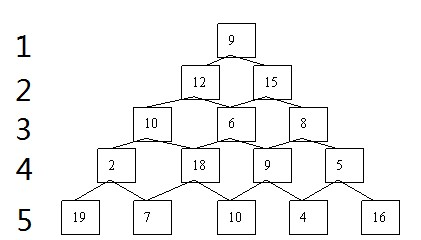
在这里插入图片描述

1.用动态规划方法解决的问题有两个特征：

（1）重叠子问题：如果一个问题可以被分解为若干个子问题，且这些子问题重复出现，那么称这个问题拥有重叠子问题。
（2）最优子结构：一个问题的最优解可以由其子问题的最优解有效的构造出来。
动态规划将一个复杂的问题分解为若干个子问题，通过综合子问题的最优解来得到原问题的最优解。需要注意的是动态规划会将每个求解过的子问题的解记录下来，下次遇到同样的子问题可以直接使用记录的结果。用这种方法提高计算效率。

思考一

从数塔顶部向下走，每次都有两种路径选择：向左下走或右下走，最简单的方法可以枚举所有路径走法，求出所有路径中到达底层时走过的最大值。可以由dfs递归搜索的方式设计程序（时间复杂度为指数级）
dfs(i,j)表示从第i层第j个元素出发到达最底层时走过路径的最小和。dfs(1,1)就是我们要求的结果。
在这里插入图片描述

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int f[100][100];
int dfs(int i,int j){
    if(i==n) return f[i][j];         //走到最底层直接返回底层数字结果
    else{
        int ans1=dfs(i+1,j)+f[i][j];  //向左下方走
        int ans2=dfs(i+1,j+1)+f[i][j];//向右下方走
        return max(ans1,ans2);
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>f[i][j];
        }
    }
    cout<<dfs(1,1)<<endl;
    return 0;
}

递归的方式实现动态规划

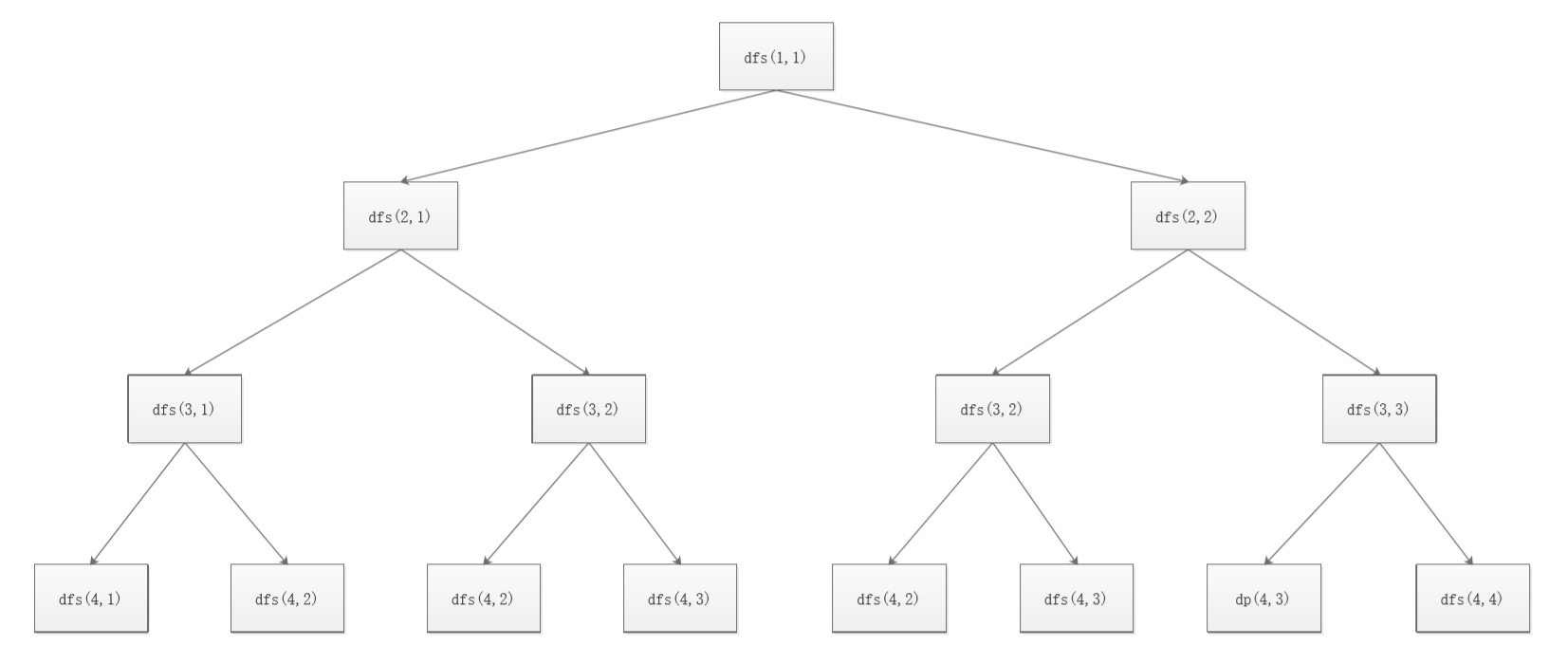
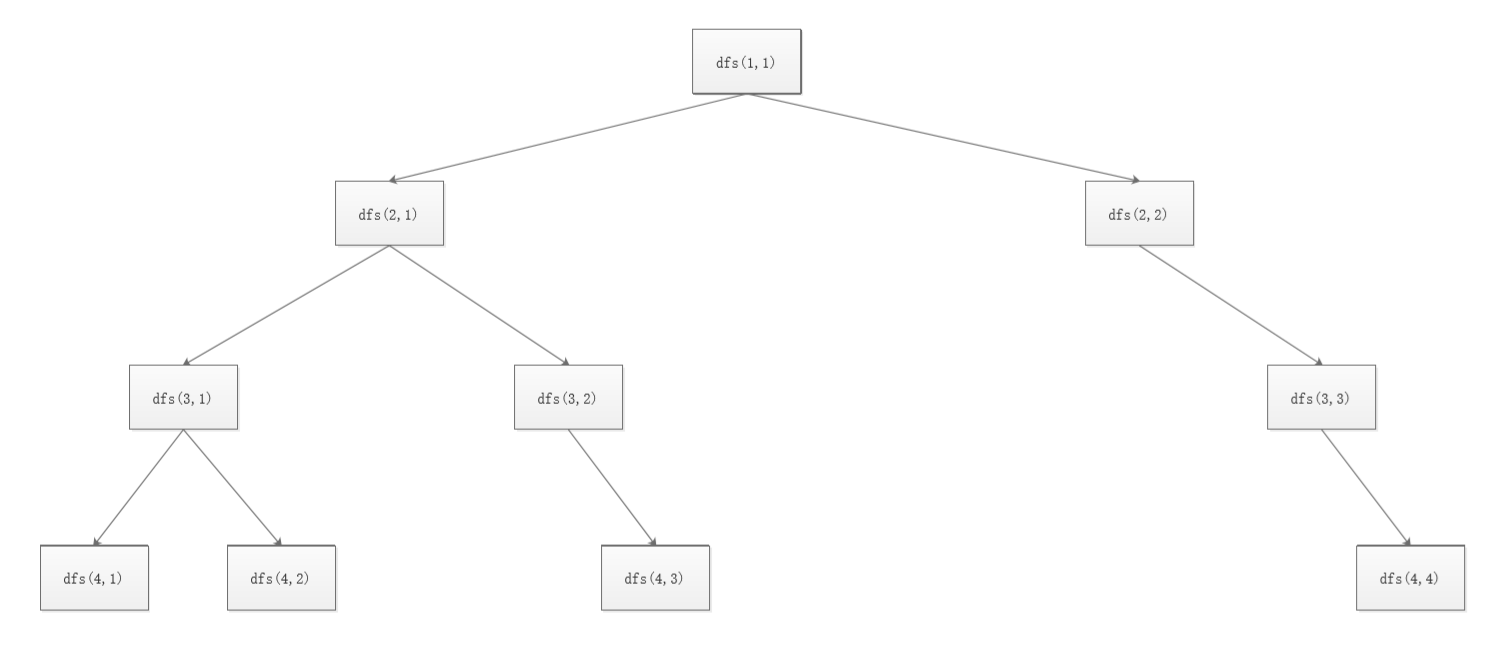
直接搜索会有重叠子问题，我们画出状态搜索树:可以看出dp(3,2),dp(4,2),dp(4,3)被重复计算。因此我们可以保存每次搜索时的结果，避免重复计算。即用数组dp[i][j]记录dfs(i,j)每次搜索时的结果,这种记录结果再利用的方式称为记忆化搜索。可以看出避免了重复计算，时间复杂度为O（n）。
动态规划会将每个求解过的子问题的解记录下来，下次遇到同样的子问题可以直接使用记录的结果。这种用递归实现的方式就成为记忆化搜索。我们要求解的问题是dfs(1,1)。求解问题直接从dfs(1,1)出发向下计算，这种递归向下搜索的方式称为自顶向下的方法。
在这里插入图片描述

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int f[100][100],m[100][100];
int dp(int i,int j){
    if(i==n) return f[i][j];
    if(m[i][j]!=-1) return m[i][j];
    else{
        m[i][j]=max(dp(i+1,j),dp(i+1,j+1))+f[i][j];
        return m[i][j];
    }
}
int main()
{
    cin>>n;
    ///记忆化搜索
    fill(m[0],m[0]+100*100,-1);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>f[i][j];
        }
    }
    cout<<dp(1,1)<<endl;
    return 0;
}

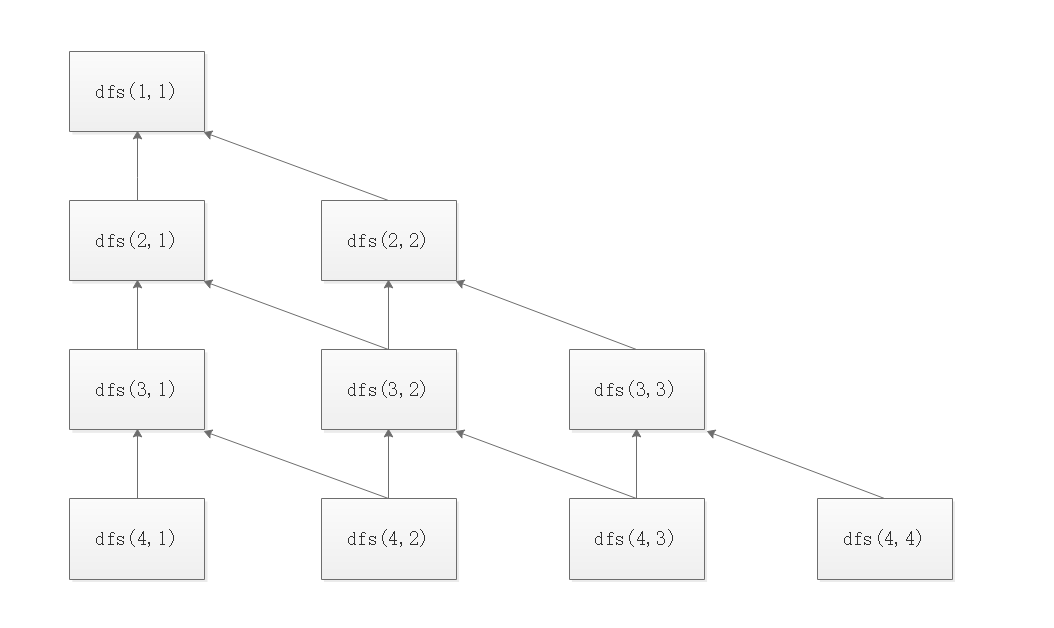
递推的方式实现动态规划

1.寻找递推表达式：令dp[i][j]表示从第i行第j个数字出发的到达最底层的所有路径中的最大和。
2.要求解从位置（1,1）出发到达最底层的最大和dp[1][1],那么一定要计算它的两个子问题:“从位置（2,1）到达最底层的最大和dp[2][1]”和从“从位置（2,2）到达最底层的最大和dp[2][2]”。，即进行了一次决策：向左下走还是右下走。可以推出状态转移方程：
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j]; dp[i][j]称为问题的状态，可以知道数塔最后一层值总是等于元素本身（dp[n][j]=f[n][j]）,而动态规划的递推写法正是从这些边界出发，通过状态转移方程扩散到整个数组。
3.这种从边界开始不断向上解决问题，直到解决了目标问题的计算方式称为自底向上的计算方式。
在这里插入图片描述

#include<iostream>
#include<cstring>
using namespace std;
int n;
int f[100][100],dp[100][100]={0};
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>f[i][j];
        }
    }
    //初始化边界
    for(int j=1;j<=n;j++){
        dp[n][j]=f[i][j];
    }
    for(int i=n-1;i>=1;i--){
        for(int j=1;j<=n;j++){
            dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+f[i][j];
        }
    }
    cout<<dp[1][1]<<endl;
    return 0;
}