数塔问题（C语言）

104 阅读 0 评论 69 点赞

我是靠谱客的博主害怕咖啡豆，最近开发中收集的这篇文章主要介绍数塔问题（C语言），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目：如下图出示了一个数字三角形，请编写一个程序计算从顶自底的某一条路径，使该路径经过的数字总和最大。（动态规划问题）

每一步可沿左斜线向下或右斜线向下
三角形行数（1~100，不一定是如图中的5行）
三角形中数字为整型

动态规划是一种通过将原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划的求解方式大多是递推，也会有一些问题必须用递归求解，通常首先确定问题的状态表示，再推出状态之间的转移方程，从而求出最终状态的解。

动态规划的前提：

最优子结构：局部最优解能够决定全局最优解（通常需要多个局部最优来决定全局解）
无后效性：子问题的解一旦确定，就不会再因为其它子问题的求解而改变
重叠子问题：对于必须要用递归求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次，通过记录子问题的解而提升效率

递推算法：

#include<iostream>
using namespace std;

int main(){
	int n; //行数 
	int a[100][100];	
	do{
		cout<<"请输入数塔的行数(1<n<=100)：";
		cin>>n;	
	}while(n <= 1 || n > 100);
	
	cout<<"请按行依次输入数塔中的值(整型，第i层有i个节点)："<<endl;
	for(int j = 0; j < n; j++){          //用下三角形存数塔
		for(int i = 0; i <= j; i++){
			cin>>a[j][i];
		}
	}
	//递推算法(自底向上运算)：
	for(int i = n-2; i >= 0; i--){
		for(int j = 0; j <= n-2; j++){
			a[i][j] += (a[i+1][j] > a[i+1][j+1])?(a[i+1][j]):(a[i+1][j+1]);
		}
	}  
	cout<<"最大路径的值："<<a[0][0]<<endl;
}

递归算法：

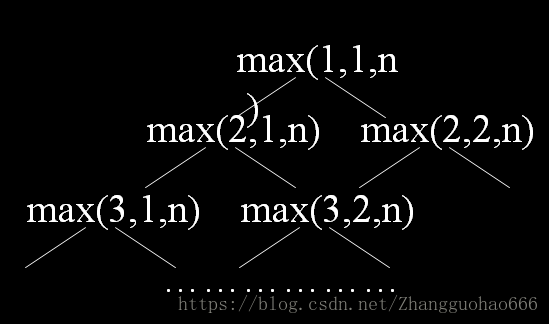
在这里插入图片描述

#include<iostream>
using namespace std;

int a[100][100];   //数塔放在全局里面 

//递归算法（自顶向下） 

int max(int i, int j, int n){
	int left, right;
	if (i == n-1) //到达底层
         return a[i][j];
    left = max(i+1,j,n); //左边
    right = max(i+1,j+1,n); //右边
    return (left>right) ? (left+a[i][j]) : (right+a[i][j]);
	//这个算法，路径中的许多值被重复计算了（重叠子问题） 
} 

int main(){
	int n; //行数 		
	do{
		cout<<"请输入数塔的行数(1<n<=100)：";
		cin>>n;	
	}while(n <= 1 || n > 100);
	
	cout<<"请按行依次输入数塔中的值(整型，第i层有i个节点)："<<endl;
	for(int j = 0; j < n; j++){
		for(int i = 0; i <= j; i++){
			cin>>a[j][i];
		}
	}
	cout<<"最大路径的值:"<<max(0,0,n)<<endl;	
}

记忆性递归（解决重叠子问题）：

#include<iostream>
using namespace std;

#define MarkerValue -1 //MarkerValue是标记值，假定标记值为 -1 
					    
int a[100][100], //数塔放在全局里面 
	f[100][100];	   //存储中间计算结果，如果是标记值（-1）则继续计算，
	 				   //如果不是标记值（-1），直接返回，避免重复计算 

int max(int i, int j, int n){
	int left, right;
	
	if (i == n-1) f[i][j] = a[i][j]; 
	if (f[i][j] != -1) return f[i][j];
	left = max(i+1,j,n); //左边
	right = max(i+1,j+1,n); //右边
	
    return (left > right) ? (left + a[i][j]) : (right + a[i][j]);
} 

int main(){
	int n; //行数 		
	do{
		cout<<"请输入数塔的行数(1<n<=100)：";
		cin>>n;	
	}while(n <= 1 || n > 100);
	
	cout<<"请按行依次输入数塔中的值(整型，第i层有i个节点)："<<endl;
	for(int j = 0; j < n; j++){
		for(int i = 0; i <= j; i++){
			cin>>a[j][i];
			f[j][i] = MarkerValue;  //把标记值放到f[][]中 
		}
	}
	
	cout<<"最大路径的值:"<<max(0,0,n)<<endl;	
}