数据结构-二维数组-三角矩阵压缩存储

一、什么是三角矩阵

前情提要

三角矩阵也是属于一类特殊的二维数组矩阵，同样也用压缩的存储方式，能够更好的节约存储空间，二维数组的三角矩阵分为上三角矩阵和下三角矩阵，其实现的原理差不多类似，下面就细细道来。

三角矩阵的特点

此处讨论的三角矩阵的行数和列数是一样的，不妨设都设为$n$。如下所示：

$$begin{bmatrix} {a_{11}}&{a_{12}}&{a_{13}}&{a_{14}}&cdots&{a_{1n-1}}&{a_{1n}}\ {}&{a_{22}}&{a_{23}}&{a_{24}}&cdots&{a_{2n-1}}&{a_{2n}}\ {}&{}&{a_{33}}&{a_{34}}&cdots&{a_{3n-1}}&{a_{3n}}\ {}&{}&{}&{a_{44}}&cdots&{a_{4n-1}}&{a_{4n}}\ {}&{}&delta&{}&ddots&vdots&vdots\ {}&{}&{}&{}&{}&{a_{n-1n-1}}&{a_{n-1n}}\ {}&{}&{}&{}&{}&{}&{a_{nn}} end{bmatrix}$$
如上所示，为上三角矩阵，矩阵的对角线以下的所有元素均为同一常数$delta$,或者无效的数据。从上往下逐行的元素总数是比上一行少一个，构成等差数列条件，以下会用的等差数列数学知识。若$delta$为常数，则需要在所有元素的最后一个另外加一个元素位置单独存放该数据，毕竟只要是有效数据就需要存储的嘛。对于下三角矩阵有类似的特点，这里放到公式推导里面去介绍。

二、三角矩阵压缩存储

上三角矩阵的存储

如下所示：

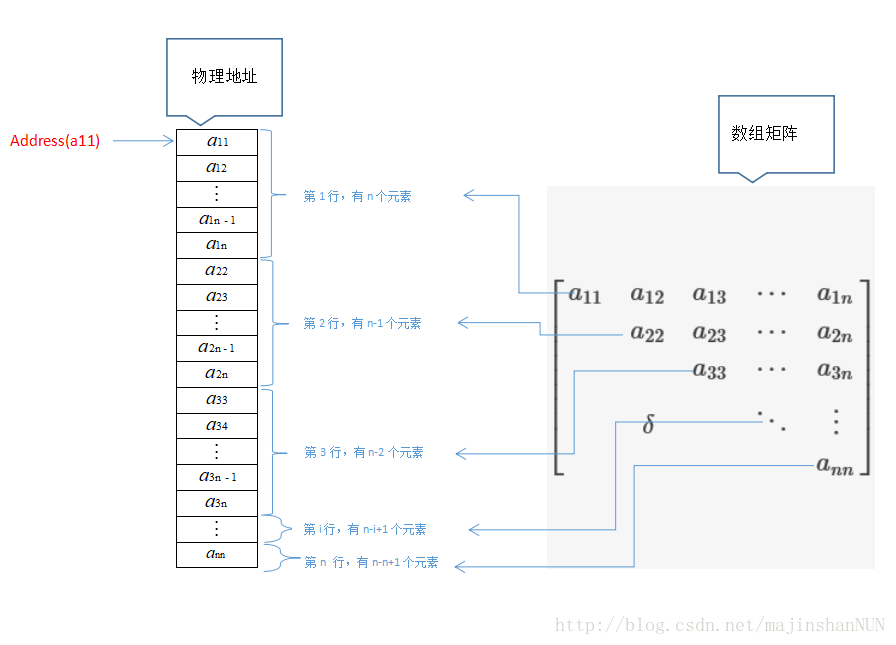
对于元素处于上三角区域，即元素$a_{ij}$，其中$i le j$，可得如下规律：
第$1$行有$n$个元素，第$2$行有$(n-1)$个元素，第$3$行有$(n-2)$个元素，第$i$行有$(n-i+1)$个元素，…第$n$行有$(n-n+1)$(即只有$1$个元素)个元素；可得对于元素$a_{ij}$，第$(i-1)$行（即元素$a_{ij}$前一行）共有：

$$sum_{k=1}^{i-1}(n-k+1)=frac {(i-1)(2n-i+2)}{2}$$ 个元素，元素 ${a_{ij}}$,在第i行中是第 $(j-i+1)$个元素，规定：每个元素所占的长度为 $e$，所以： $$address({a_{ij}})=address({a_{11}})+(frac {(i-1)(2n-i+2)}{2}+j-i)e$$
对于元素处于下三角区域，即元素 $a_{ij}$，其中 $i gt j$，因为下三角区的元素值都一样（如果元素的值有效），则把它放到存储区的最后一个单元,即： $frac {(n+1)n}{2}+1$的位置，可得地址公式： $$address(a_{ij})=address(a_{11})+(frac {(n+1)n}{2})e$$

下三角矩阵的存储

如下所示：

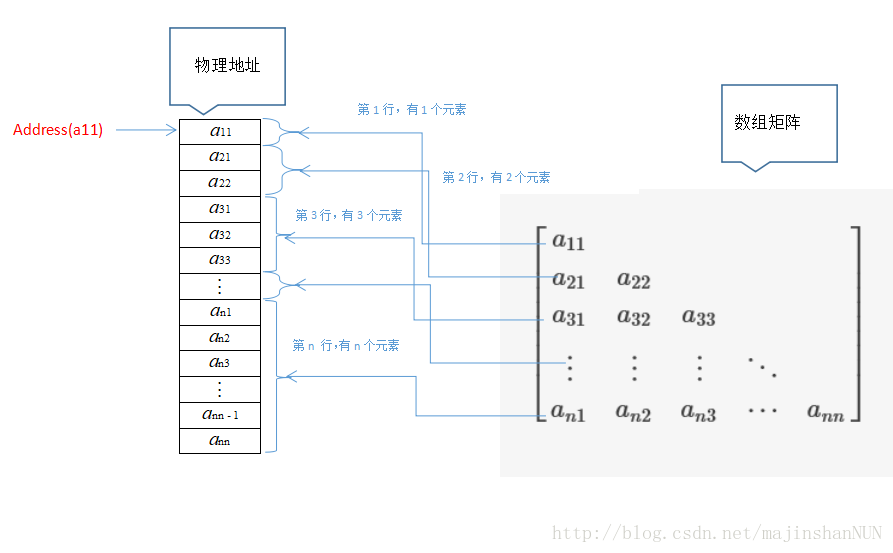
对于元素处于下三角区域，即元素$a_{ij}$，其中$i ge j$，可得如下规律：
第$1$行有$1$个元素，第$2$行有$2$个元素，第$3$行有$3$个元素，第$i$行有$i$个元素，…第$n$行有$n$个元素；可得对于元素$a_{ij}$，第$(i-1)$行（即元素$a_{ij}$前一行）共有：

$$sum_{k=1}^{i-1}k=frac {(i-1)(1+i-1)}{2}=frac {(i-1)i}{2}$$ 个元素,元素 ${a_{ij}}$在第 $i$行为第$j$个元素，现规定每个元素占用的单位为 $e$，可得：
$$address({a_{ij}})=address({a_{11}})+(frac {(i-1)i}{2}+j-1)e$$ ,对于上三角区的元素将其放到存储区的最后一个单元，即 $frac {(n+1)n}{2}+1$的位置，可得地址公式： $$address(a_{ij})=address(a_{11})+(frac {(n+1)n}{2})e$$ ，和上三角存储的一样。

矩阵的压缩存储暂时写到这，写得不好，多多指教哈。

最后

以上就是沉静灰狼为你收集整理的数据结构-二维数组-三角矩阵压缩存储数据结构-二维数组-三角矩阵压缩存储二、三角矩阵压缩存储的全部内容，希望文章能够帮你解决数据结构-二维数组-三角矩阵压缩存储数据结构-二维数组-三角矩阵压缩存储二、三角矩阵压缩存储所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。