【注】致力于将知识讲明白！不懂请留言！

基本概念

压缩存储

指为多个值相同的元素只分配一个存储空间，而对于零元素不分配空间，其目的就是节省存储空间；

特殊存储

指具有很多相同的元素或者零元素，并且这些元素的分布具有一定的规律；常见的一些特殊矩阵有：对称矩阵，上（下）三角矩阵和对角矩阵。
特殊矩阵的压缩存储方法：找出特殊矩阵中值相等的元素的分布规律，把那些呈现规律性分布的，值相同的多个矩阵元素压缩存储到一个存储空间中：

下面介绍三种特殊矩阵

1.对称矩阵

在一个 n 阶方阵中，有$a_{ij}$ = $a_{ji}$ (即各数据元素沿主对角线对称的矩阵)，其中 1≤i，j≤n，则称该矩阵为对称矩阵，针对与这类矩阵，我们只需要存储上三角区或者下三角区就可以；
设有对称矩阵A[i][j]如下图示：

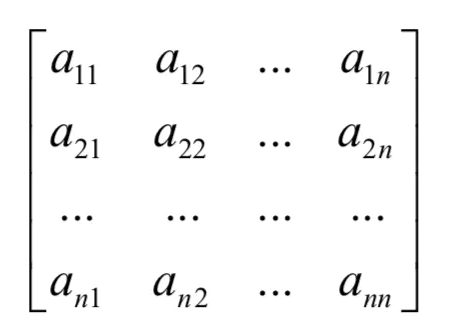
针对这种n阶对称方针n阶对称矩阵A，上三角区元素和下三角区元素的对应元素是相同的，若仍采用二维数组存放，则会浪费一半的存储空间。为此我们将该对称矩阵存放再一维数组B中，形式如下（只存放下三角部分元素）：
在数组B中，位于元素$a_{ij}$（i >= j）前面的元素个数为：
第 1 行：1个元素（$a_{1,1}$）；
第 2 行：2个元素（$a_{2,1}$，$a_{2,2}$）；
…
第 i-1 行：i-1 个元素（$a_{i-1,1}$，$a_{i-1,2}$，…，$a_{i-1,i-1}$） ;
第 i 行：j-1 个元素（$a_{i,1}$，$a_{i,2}$，…，$a_{i,j-1}$）;
由上面我们可以看出元素$a_{ij}$在数组B中的下标 k = 1+2+…+ （(i-1 )+（(j-1)=i(i-1)/2 + j-1；
因此元素下标之间的对应关系如下：

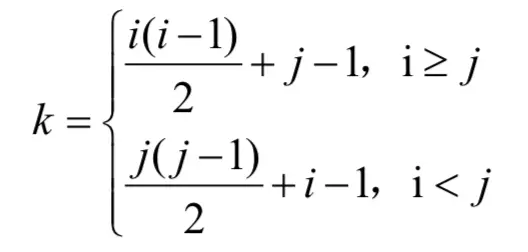
【注】数组下标从0开始；

2.三角矩阵

三角矩阵分为上三角矩阵和下三角矩阵，这个是根据是上三角区还是下三角区素有元素为同一常量来区分。

2.1下三角矩阵
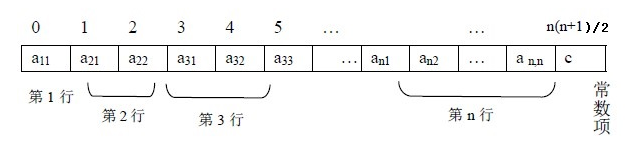
下三角矩阵是指上三角区所有元素均为同一常量，设有下三角矩阵 A[i][j]如下图所示：

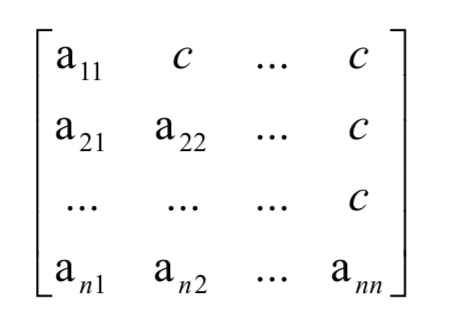
我们可以看出其存储思想和对称矩阵是类似的，不同的地方在于存储完不同的元素后，需要存储其他相同元素一次，故可以讲三角矩阵A[1…n][1…n]压缩存储在B[n(n+1)/2 + 1]中；
在下三角矩阵中,元素下标之间对应关系为：

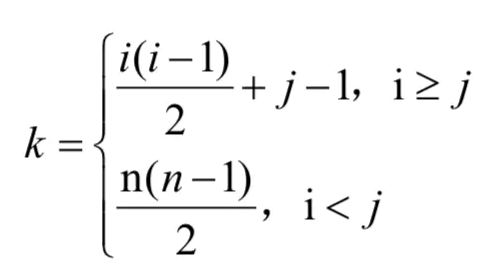
下三角矩阵在内存中的压缩存储形式如下：

2.2上三角矩阵
上三角矩阵是指下三角区所有元素均为同一常量，设有下三角矩阵 A[i][j]如下图所示：

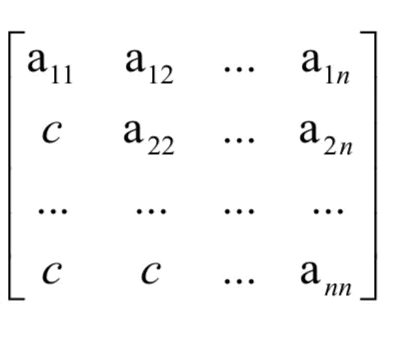
我们可以看出在存储上三角矩阵只需要存储上三角区，主对角线和下三角区的常量一次，可将其压缩存储在B[n(n+1)/2 + 1]；
我们来分析一下：
在数组B中，位于元素$a_{ij}$（i =< j ）前面的元素个数为：
第 1 行：n 个元素；
第 2 行： n -1 个元素；
…
第 i-1 行：n - i +2 个元素；
第 i 行：j - i 个元素；
因此，元素$a_{ij}$在数组B中的下标 k = n +(n-1) +…+(n-i+2) + (j-i+1) -1 = (i-2)(2n-i+2)/2 + (j-i)；
所以元素下标之间的对应关系如下：

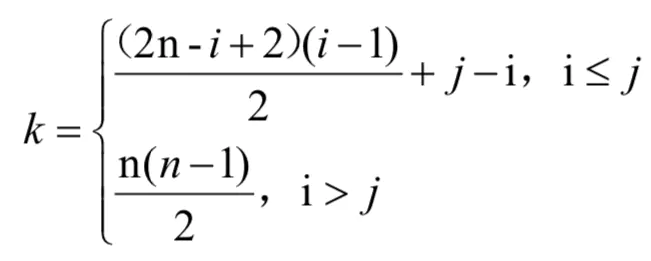
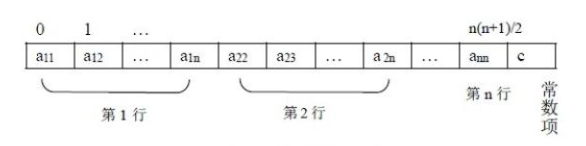
上三角矩阵在内存中的压缩存储形式如下：

【注】以上推导均假设数组的下标从0开始；

3.三对角矩阵

三对角矩阵也称带状矩阵，它是指所有非零元素都集中在以主对角线为中心的3条对角线的区域，其他区域均为零的矩阵；设有三对角矩阵 A[i][j]如下图所示：

三对角矩阵采用压缩存储时，是将3条对角线上的元素$a_{ij}$（1=<i，j= <n，|i - j| =<1）在一维数组B中存放下标为 k = 2i + j - 3；
三对角矩阵在内存中的压缩存储形式如下：

4.稀疏矩阵

如果一个矩阵中的非零元素的个数 t 相对于矩阵元素的个数 s 来说非常的少，此时我们就说该矩阵为稀疏矩阵；所以说如果采用正常的存储方法，那是非常浪费存储空间的，因此我们可以只存储非零元素，但又不像前面所讲的矩阵，这里的非零元素是没有规律的，而且仅仅存储非零元素的值是不够的，还需要存储它所在的行和列，那么根据这些我们想到可以将这些非零元素及其相应的行和列构成一个三元组（行标，列标，值）如下：

那构成三元组的稀疏矩阵就可以采用数组或者十字链表法存储了；
【注】稀疏矩阵压缩存储后就失去了随机存取的特性；

最后

以上就是超帅枫叶为你收集整理的特殊矩阵的压缩存储基本概念下面介绍三种特殊矩阵的全部内容，希望文章能够帮你解决特殊矩阵的压缩存储基本概念下面介绍三种特殊矩阵所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。