一.三角矩阵的概念

以主对角线划分三角矩阵有下三角矩阵和上三角矩阵

下三角矩阵：矩阵(除主对角线)的上三角部分的值均为一个常数C或者0

上三角矩阵：与下三角矩阵相反

图示：（图中蓝色主对角线部分元素（一般情况）永远不都为一个常数或者0）

二.压缩原理

根据上、下三角矩阵的特殊性(有一小半部分的元素都为一个常数C或者0)我们可以考虑将这一半的空间压缩到一个元素（多对一的映射)，然后另一半的部分就类似对称矩阵一半部分的压缩存储了。

三.矩阵坐标[i,j]转换为一维数组下标K的方法

1>下三角矩阵：

(1).首先考虑，非重复部分的存储，见图：

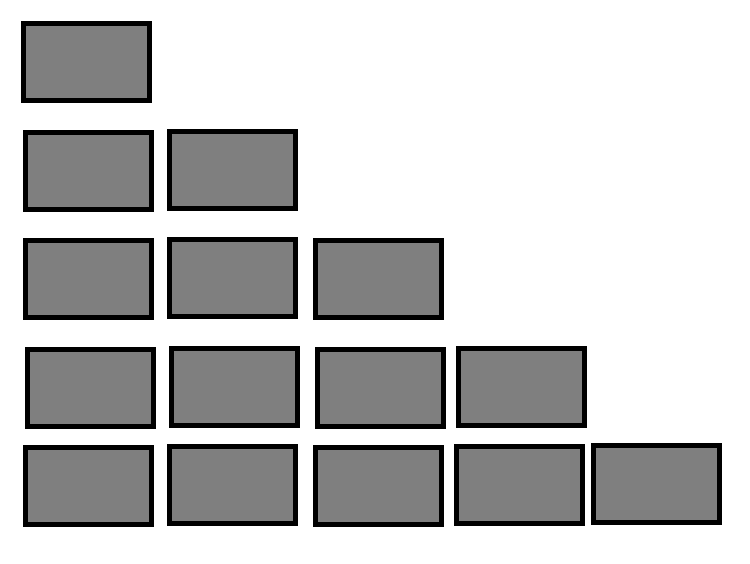
可以得出k = i(i-1)/2+j-1 （推导过程可以参考：对称矩阵的压缩https://blog.csdn.net/SWEENEY_HE/article/details/85951555）

(2).重复部分只需一个元素即可，为不影响前面的存储，考虑放到所有非重复元素的后面即可， 由于前面部分总共的元素个数为：

n(1+n)/2(等差数列求和，每行元素逐级递增）又由于数组以0为起点，所以放到n(1+n)/2的位置即可。

总结：

k = i(i-1)/2+j-1 (i<=j)  

k = n(n+1)/2 (i>j)   

2>上三角矩阵

(1).先考虑非重复部分的存储，图示：

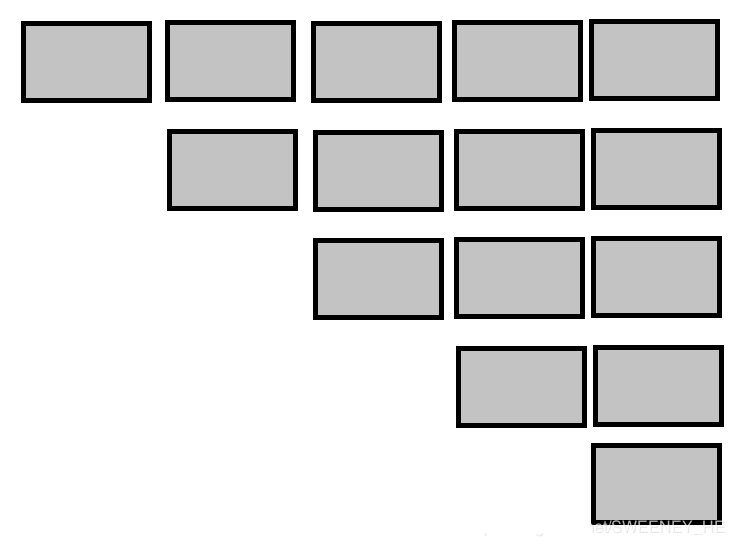
按行优先存储，矩阵中元素对应一维数组的元素规则为：

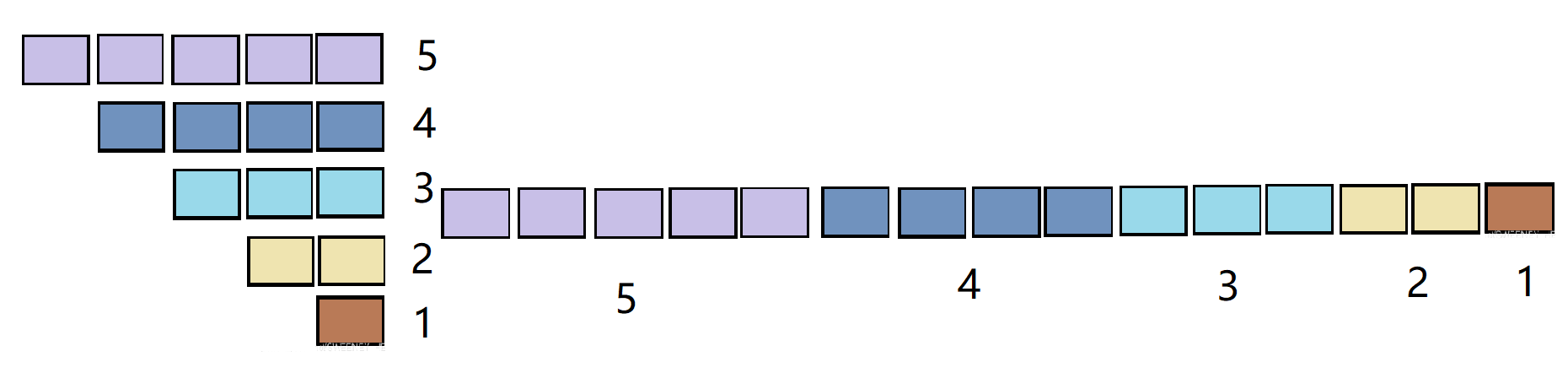
由图显而易见，某元素在一维数组中的下标就是它按行优先存储时在半个矩阵中的序号

(1-1)序号 = 所有在它前面元素的个数 = 它所在行前面行的所有元素+它所在行它前面的元素

由于每行元素个数逐级递减，构成一个等差数列，公差：d = 1,首项：a1 = n ,末项：an = n-(i-1) = n-i+1（经评论区提醒，已自纠）

(1-2)前i-1行元素个数为：sn = n(a1+an)/2 = (i-1){n+[n-(i-1)+1]}/2=(i-1)(2n-i+2)/2  

(1-3)第i行中在它前面的元素个数为：j-i  （元素逐行减少，可以看成从行首拿掉一个元素，所以第i行已经被拿走了i-1个元素，第i行的第j列元素前面就只有(j-1)-(i-1) = j-i个元素了）

(1-4)公式：K =(i-1)(2n-i+2)/2+j-i

(2).考虑重复部分元素和下三角一样：k = n(n+1)/2

总结：

K = (i-1)(2n-i+2)/2+j-i(i<=j)

K = n(n+1)/2 (i>j)

最后

以上就是拉长嚓茶为你收集整理的数据结构----三角矩阵压缩存储中下标的计算一.三角矩阵的概念二.压缩原理三.矩阵坐标[i,j]转换为一维数组下标K的方法的全部内容，希望文章能够帮你解决数据结构----三角矩阵压缩存储中下标的计算一.三角矩阵的概念二.压缩原理三.矩阵坐标[i,j]转换为一维数组下标K的方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。