概述
相信朋友们对矩阵应该不陌生，它贯穿了几乎所有计算机应用数学的所有课程。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。下面我们简单复习下。
什么是矩阵
1.矩阵定义
在数学中，矩阵（Matrix）是一个按照长方阵列排列的实数或复数的集合，最早来自于方程组的系数及常数所构成的方阵。
由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：
图1 矩阵
这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。而行和列都为n的矩阵我们称为n阶方阵。
2.对称矩阵
如果n阶矩阵中的元素满足： aij = aji ( i 为行标， j 为列标)，就称这个矩阵为对称矩阵。
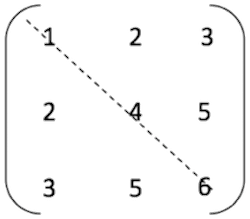图2 对称矩阵
图1 为 3 阶对称矩阵，图中的虚线为矩阵的 “主对角线” ，主对角线上方区域称为 “上三角” ；主对角线下方称为 “下三角” ，沿主对角线对称的数据元素一一相等。
3.上下三角矩阵
上下三角矩阵，和对称矩阵类似，不同在于，上三角矩阵是指主对角线下方的元素（不包括主对角线上的）都是常数C（包括数值 0 ）；同理，下三角矩阵是指主对角线上方的元素都是常数C。
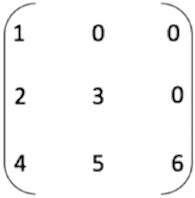图3 上三角矩阵
矩阵运算
1.矩阵转置
矩阵的转置实际上就是将数据元素的行标和列标互换，即 T(i,j) = M(j,i) 。例如：
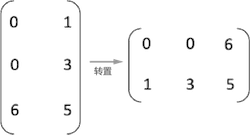图4 矩阵的转置
矩阵的转置，经历了三个步骤：
（1）矩阵的行数 n 和列数 m 的值交换；
（2）将数组中的i和j调换；
（3）转换之后的表同样按照行序（置换前的列序）为主序，进行排序；
2.矩阵加法
矩阵之间能够进行加法运算的前提条件是：各矩阵的行数和列数必须相等。矩阵相加的结果就是矩阵中对应位置的值相加所组成的矩阵，例如：
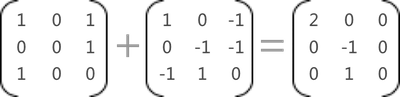图5 矩阵相加
3.矩阵乘法
矩阵相乘的前提条件是：
（1）当矩阵A的列数等于矩阵B的行数时，A与B可以相乘，且矩阵的乘法运算没有交换律，即 A*B 和 B*A 是不一样的。。
（2）矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
（3）乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。
如下所示：
矩阵基本运算封装
上面我们了解了矩阵的几个基本概念和运算，下面我将用Java的类封装来实现一个矩阵的基本运算。
public class Matrix {
private int[][] matrix;//矩阵数组容器
public Matrix(int rowNum,int colNum){
this.matrix=new int[rowNum][colNum];
}
public Matrix(int [][] arr){
this.matrix=arr;
}
//设置第row行第col列的值
public void set(int row,int col,int val){
this.matrix[row][col]=val;
}
//获取第row行第col列的值
public int get(int row,int col){
return this.matrix[row][col];
}
//数组转置
public Matrix transpose(){
int listNum = this.matrix[0].length; //列数
int lineNum = this.matrix.length; //行数
int [][] matrix = new int [listNum][lineNum];//构建转置后的数组
for (int i = 0; i < lineNum; i++) {
for (int j = 0; j < listNum; j++) {
matrix[j][i] = this.matrix[i][j];
}
}
return new Matrix(matrix);
}
//判断矩阵是上三角矩阵
public boolean isUpperTriangularMatrix() {
for(int i=1;i<this.matrix.length; i++){
for(int j=0;j<i;j++){
if(this.matrix[i][j] !=0){
return false;
}
}
}
return true;
}
//判断一个矩阵是否为下三角矩阵
public boolean isLowerTriangularMatrix(){
for(int i=0; i<this.matrix.length-1; i++){
for(int j=i+1; j<this.matrix[0].length; j++){
if(this.matrix[i][j] != 0){
return false;
}
}
}
return true;
}
//判断一个矩阵是否为对称矩阵
public boolean isSymmetricMatrix() {
int i,j;
for(i=1;i<this.matrix.length;i++){
for(j=0;j<i;j++){
if(this.matrix[i][j] != this.matrix[j][i]){
return false;
}
}
}
return true;
}
//矩阵加法
public Matrix plus(Matrix obj){
int[][] result = new int[obj.matrix.length][obj.matrix[0].length];
for(int i = 0; i < obj.matrix.length; i++){
for(int j = 0; j < obj.matrix[0].length; j++){
result[i][j] = this.matrix[i][j] + obj.matrix[i][j];
}
}
return new Matrix(result);
}
//矩阵相乘
public Matrix multiplict(Matrix obj){
int[][] result= new int[this.matrix.length][obj.matrix.[0].length];
for(int i = 0; i < this.matrix.length; i++){
for(int j = 0;j < obj.matrix.[0].length; j++){
result[i][j] = this.calculateSingleResult(this.matrix, obj.matrix, i, j);
}
}
return new Matrix(result);
}
/**
* 矩阵乘法a中result每个元素的单一运算
* @param matrix_a 矩阵a
* @param matrix_b 矩阵b
* @param row 参与单一运算的行标
* @param col 参与单一运算的列标
* @return result 运算结果
*/
private int calculateSingleResult(int[][] matrix_a, int[][] matrix_b, int row, int col){
int result = 0;
for(int i = 0; i < matrix_a[0].length; i++){
result += matrix_a[row][i] * matrix_b[i][col];
}
return result;
}
// 将矩阵输出
public void output() {
for (int i = 0; i < this.matrix.length; i++) {
for (int j = 0; j < this.matrix[i].length; j++) {
System.out.print(this.matrix[i][j] + "t") ;
}
System.out.println() ;
}
}
}上面的Matrix类就是一个简单的矩阵操作类，这里只是作为一个参考实例，有些逻辑不是很严格，需要的可以自行修改。
最后
以上就是冷艳季节为你收集整理的数据结构和算法--Java实现矩阵的全部内容，希望文章能够帮你解决数据结构和算法--Java实现矩阵所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复