1.1.knn对象实现
注意
下面的这段代码中，只需在命令行运行这个脚本bash get_datasets.sh，下载数据即即可。其他的应该是和Google云有关

# This mounts your Google Drive to the Colab VM.
from google.colab import drive
drive.mount('/content/drive', force_remount=True)

# Enter the foldername in your Drive where you have saved the unzipped
# assignment folder, e.g. 'cs231n/assignments/assignment1/'
FOLDERNAME = None
assert FOLDERNAME is not None, "[!] Enter the foldername."

# Now that we've mounted your Drive, this ensures that
# the Python interpreter of the Colab VM can load
# python files from within it.!bash
import sys
sys.path.append('/content/drive/My Drive/{}'.format(FOLDERNAME))

# This downloads the CIFAR-10 dataset to your Drive
# if it doesn't already exist.
%cd drive/My Drive/$FOLDERNAME/cs231n/datasets/
!bash get_datasets.sh
%cd /content/drive/My Drive/$FOLDERNAME

---------------------------------------------------------------------------

ModuleNotFoundError                       Traceback (most recent call last)

<ipython-input-4-df8148eadd1c> in <module>
      1 # This mounts your Google Drive to the Colab VM.
----> 2 from google.colab import drive
      3 drive.mount('/content/drive', force_remount=True)
      4 
      5 # Enter the foldername in your Drive where you have saved the unzipped


ModuleNotFoundError: No module named 'google'

k-Nearest Neighbor (kNN) exercise

Complete and hand in this completed worksheet (including its outputs and any supporting code outside of the worksheet) with your assignment submission. For more details see the assignments page on the course website.

The kNN classifier consists of two stages:

• During training, the classifier takes the training data and simply remembers it
• During testing, kNN classifies every test image by comparing to all training images and transfering the labels of the k most similar training examples
• The value of k is cross-validated

In this exercise you will implement these steps and understand the basic Image Classification pipeline, cross-validation, and gain proficiency in writing efficient, vectorized code.

# Run some setup code for this notebook.

import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt

# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0)     # 显示图像的最大范围
plt.rcParams['image.interpolation'] = 'nearest'  # 差值方式，设置 interpolation style
plt.rcParams['image.cmap'] = 'gray' # 灰度空间

# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

pwd

'/home/chenchao/workspace/cs231n.github.io/assignments/2021/assignment1'

# Load the raw CIFAR-10 data.
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'

# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
   del X_train, y_train
   del X_test, y_test
   print('Clear previously loaded data.')
except:
   pass

X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

# sanity check  -  完整性检查，可以理解为为了保险起见再次检查
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)

Clear previously loaded data.
Training data shape:  (50000, 32, 32, 3)
Training labels shape:  (50000,)
Test data shape:  (10000, 32, 32, 3)
Test labels shape:  (10000,)

# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):  # y是类别的索引，cls是列表的值
    idxs = np.flatnonzero(y_train == y)   # np.flatnonzero得到数组中非零元素的索引，其实这里就是找出训练集标签中与上面的列表相同的元素索引
    idxs = np.random.choice(idxs, samples_per_class, replace=False)  # 在这些索引中随机选出7个索引
    for i, idx in enumerate(idxs):   # 这里的绘图是按列绘图，即每一类的7张图片排成一列
        plt_idx = i * num_classes + y + 1   # i是绘图的第几行，也就是这类的7张图片中的第几张；y是列，也就是这是第几类的图片；+1是索引从1开始
        plt.subplot(samples_per_class, num_classes, plt_idx)  # 参数分别是 （行数，列数，序号），注意序号是从左向右数，到头换到下一行继续数
        plt.imshow(X_train[idx].astype('uint8'))  # 绘制图片，astype强制转化一下。经测试这句必须加，否则显示的图片不正常
        plt.axis('off')
        if i == 0:
            plt.title(cls)
plt.show()

print(range(10))

range(0, 10)

# Subsample the data for more efficient code execution in this exercise
# 在本练习中对数据进行二次采样以更有效地执行代码——即降低数据量，加快运算
num_training = 5000
mask = list(range(num_training))  # 生成0-5000的列表，注意这里range是生成一个生成器对象，需要list转化成列表。这和py2不同
X_train = X_train[mask]   # 使用列表选择数据 ？？？直接切片选择数据不行吗
y_train = y_train[mask]

num_test = 500
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]

# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))   # 将X_train数组进行维度变换，假设一个数据对象narray的总元素个数为N，如果我们给出一个维度为（m，-1）时，我们就理解为将对象变换为一个二维矩阵，矩阵的第一维度大小为m，第二维度大小为N/m。
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)

(5000, 3072) (500, 3072)

from cs231n.classifiers import KNearestNeighbor

# Create a kNN classifier instance. 
# Remember that training a kNN classifier is a noop: 
# the Classifier simply remembers the data and does no further processing 
classifier = KNearestNeighbor()
classifier.train(X_train, y_train)

We would now like to classify the test data with the kNN classifier. Recall that we can break down this process into two steps:

1. First we must compute the distances between all test examples and all train examples.
2. Given these distances, for each test example we find the k nearest examples and have them vote for the label

Lets begin with computing the distance matrix between all training and test examples. For example, if there are Ntr training examples and Nte test examples, this stage should result in a Nte x Ntr matrix where each element (i,j) is the distance between the i-th test and j-th train example.

Note: For the three distance computations that we require you to implement in this notebook, you may not use the np.linalg.norm() function that numpy provides.

First, open cs231n/classifiers/k_nearest_neighbor.py and implement the function compute_distances_two_loops that uses a (very inefficient) double loop over all pairs of (test, train) examples and computes the distance matrix one element at a time.

# Open cs231n/classifiers/k_nearest_neighbor.py and implement
# compute_distances_two_loops.

# Test your implementation:
dists = classifier.compute_distances_two_loops(X_test)
print(dists.shape)

(500, 5000)

# We can visualize the distance matrix: each row is a single test example and
# its distances to training examples
# 将距离矩阵可视化，越黑表示距离越接近，越白表示距离越远
plt.imshow(dists, interpolation='none')  
plt.show()

Inline Question 1

Notice the structured patterns in the distance matrix, where some rows or columns are visible brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)
注意距离矩阵中的结构化图案，其中某些行或列的可见亮度更高。 （请注意，使用默认的配色方案，黑色表示低距离，而白色表示高距离。）

数据中哪些是明显亮行背后的原因？
是什么原因造成了列？

• What in the data is the cause behind the distinctly bright rows?
• What causes the columns?

$\text{Y}ourAnswer:$ fill this in.
the answer of cc

• 1.行高亮：对于测试集中的当前行所处的图片，在训练集中所有的图片都与其不太相似，距离较远；
• 2.列高亮：与行高亮同理。

# Now implement the function predict_labels and run the code below:
# We use k = 1 (which is Nearest Neighbor).
y_test_pred = classifier.predict_labels(dists, k=1)

# Compute and print the fraction of correctly predicted examples
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 137 / 500 correct => accuracy: 0.274000

You should expect to see approximately 27% accuracy. Now lets try out a larger k, say k = 5:

y_test_pred = classifier.predict_labels(dists, k=5)
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 139 / 500 correct => accuracy: 0.278000

You should expect to see a slightly better performance than with k = 1.

Inline Question 2

We can also use other distance metrics such as L1 distance.
For pixel values $p_{ij}^{(k)}$ at location $(i,j)$ of some image $I_k$,

the mean $\mu$ across all pixels over all images is $$\mu =\frac{1}{nhw}\sum _{k=1}^n\sum _{i=1}^h\sum _{j=1}^w{p}_{ij}^{(k)}$$
And the pixel-wise mean ${\mu }_{ij}$ across all images is
$${\mu }_{ij}=\frac{1}{n}\sum _{k=1}^n{p}_{ij}^{(k)}.$$
The general standard deviation $\sigma$ and pixel-wise standard deviation ${\sigma }_{ij}$ is defined similarly.

Which of the following preprocessing steps will not change the performance of a Nearest Neighbor classifier that uses L1 distance? Select all that apply.

1. Subtracting the mean $\mu$ (${\tilde{p}}_{ij}^{(k)}=p_{ij}^{(k)}-\mu$.)
2. Subtracting the per pixel mean ${\mu }_{ij}$ (${\tilde{p}}_{ij}^{(k)}=p_{ij}^{(k)}-{\mu }_{ij}$.)
3. Subtracting the mean $\mu$ and dividing by the standard deviation $\sigma$.
4. Subtracting the pixel-wise mean ${\mu }_{ij}$ and dividing by the pixel-wise standard deviation ${\sigma }_{ij}$.
5. Rotating the coordinate axes of the data.

$\text{Y}ourAnswer:$

• 1.2.3.4.5

$\text{Y}ourExplanation:$

• 1.对每张图片的所有像素都减去同一个值，L1距离显然不变
• 2.对每张图片的每个像素都减去同一个值，但是不同的像素点减去的值不一样，最后每个像素点的L1距离还是不变，总的L1距离也不变
• 3.对每张图片的所有像素减去同一个值，再除以标准差。乘除法会影响L1距离，但是并不影响L1距离的排序，故也不影响KNN的结果
• 4.解释同3
• 5.图片旋转后像素的对应位置不变，因此L1距离不变？？？

# Now lets speed up distance matrix computation by using partial vectorization
# with one loop. Implement the function compute_distances_one_loop and run the
# code below:
dists_one = classifier.compute_distances_one_loop(X_test)

# To ensure that our vectorized implementation is correct, we make sure that it
# agrees with the naive implementation. There are many ways to decide whether
# two matrices are similar; one of the simplest is the Frobenius norm. In case
# you haven't seen it before, the Frobenius norm of two matrices is the square
# root of the squared sum of differences of all elements; in other words, reshape
# the matrices into vectors and compute the Euclidean distance between them.
difference = np.linalg.norm(dists - dists_one, ord='fro')
print('One loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

One loop difference was: 0.000000
Good! The distance matrices are the same

# Now implement the fully vectorized version inside compute_distances_no_loops
# and run the code
dists_two = classifier.compute_distances_no_loops(X_test)

# check that the distance matrix agrees with the one we computed before:
difference = np.linalg.norm(dists - dists_two, ord='fro')
print('No loop difference was: %f' % (difference, ))
if difference < 0.001:
    print('Good! The distance matrices are the same')
else:
    print('Uh-oh! The distance matrices are different')

No loop difference was: 0.000000
Good! The distance matrices are the same

# Let's compare how fast the implementations are
def time_function(f, *args):
    """
    Call a function f with args and return the time (in seconds) that it took to execute.
    """
    import time
    tic = time.time()
    f(*args)
    toc = time.time()
    return toc - tic

two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
print('Two loop version took %f seconds' % two_loop_time)

one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
print('One loop version took %f seconds' % one_loop_time)

no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
print('No loop version took %f seconds' % no_loop_time)

# You should see significantly faster performance with the fully vectorized implementation!

# NOTE: depending on what machine you're using, 
# you might not see a speedup when you go from two loops to one loop, 
# and might even see a slow-down.

Two loop version took 36.649009 seconds
One loop version took 30.127894 seconds
No loop version took 0.127495 seconds

Cross-validation

We have implemented the k-Nearest Neighbor classifier but we set the value k = 5 arbitrarily. We will now determine the best value of this hyperparameter with cross-validation.

num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []
################################################################################
# TODO:                                                                        #
# Split up the training data into folds. After splitting, X_train_folds and    #
# y_train_folds should each be lists of length num_folds, where                #
# y_train_folds[i] is the label vector for the points in X_train_folds[i].     #
# Hint: Look up the numpy array_split function.                                #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

X_train_folds = np.array_split(X_train, num_folds)   
y_train_folds = np.array_split(y_train, num_folds)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}


################################################################################
# TODO:                                                                        #
# Perform k-fold cross validation to find the best value of k. For each        #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times,   #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all     #
# values of k in the k_to_accuracies dictionary.                               #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
    accuracy = []
    for i in range(num_folds):
        X_tr = np.array(X_train_folds[:i] + X_train_folds[i+1:])     
        y_tr = np.array(y_train_folds[:i] + y_train_folds[i+1:]) 
        X_val = np.array(X_train_folds[i])
        y_val = np.array(y_train_folds[i])
#         print(X_tr.shape)  
        
        X_tr = np.reshape(X_tr,(X_tr.shape[0]*X_tr.shape[1],-1))  # 数据的展开，将每张图片都展开成行向量
        y_tr = np.reshape(y_tr,(y_tr.shape[0]*y_tr.shape[1],-1))  # 数据的展开         
#         X_val = np.reshape(X_val,(X_val.shape[0],-1))  # 数据的展开   这样得到的结果是一个二维的数组，只不过只有一行
#         y_val = np.reshape(y_val,(y_val.shape[0],-1))  # 数据的展开
#         print(y_val.shape) 
#         print(X_val.shape)  
        num_val = X_val.shape[0]   # 验证集的数量
#         print(num_test)
        
        classifier.train(X_tr, y_tr)
        dists = classifier.compute_distances_no_loops(X_val)
#         print(dists.shape)
        y_val_pred = classifier.predict_labels(dists, k=k)
#         print(y_val_pred.shape)
        num_correct = np.sum(y_val_pred == y_val)
#         print(num_correct)
        accuracy.append(float(num_correct) / num_val)
        
    k_to_accuracies[k] = accuracy
        
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Print out the computed accuracies
best_acc = 0
best_k = 1
for k in sorted(k_to_accuracies):   # 为什么要对字典进行排序？
    for accuracy in k_to_accuracies[k]:  # 访问字典的K键对应的值，也就是accuracy列表
        print('k = %d, accuracy = %f' % (k, accuracy))
        if(accuracy > best_acc):
            best_acc = accuracy
            best_k = k
print("best_k = %d while the acc is %.3f"%(best_k,best_acc))

k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.239000
k = 3, accuracy = 0.249000
k = 3, accuracy = 0.240000
k = 3, accuracy = 0.266000
k = 3, accuracy = 0.254000
k = 5, accuracy = 0.248000
k = 5, accuracy = 0.266000
k = 5, accuracy = 0.280000
k = 5, accuracy = 0.292000
k = 5, accuracy = 0.280000
k = 8, accuracy = 0.262000
k = 8, accuracy = 0.282000
k = 8, accuracy = 0.273000
k = 8, accuracy = 0.290000
k = 8, accuracy = 0.273000
k = 10, accuracy = 0.265000
k = 10, accuracy = 0.296000
k = 10, accuracy = 0.276000
k = 10, accuracy = 0.284000
k = 10, accuracy = 0.280000
k = 12, accuracy = 0.260000
k = 12, accuracy = 0.295000
k = 12, accuracy = 0.279000
k = 12, accuracy = 0.283000
k = 12, accuracy = 0.280000
k = 15, accuracy = 0.252000
k = 15, accuracy = 0.289000
k = 15, accuracy = 0.278000
k = 15, accuracy = 0.282000
k = 15, accuracy = 0.274000
k = 20, accuracy = 0.270000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.282000
k = 20, accuracy = 0.285000
k = 50, accuracy = 0.271000
k = 50, accuracy = 0.288000
k = 50, accuracy = 0.278000
k = 50, accuracy = 0.269000
k = 50, accuracy = 0.266000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.270000
k = 100, accuracy = 0.263000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.263000
best_k = 10 while the acc is 0.296

# plot the raw observations
for k in k_choices:
    accuracies = k_to_accuracies[k]
    plt.scatter([k] * len(accuracies), accuracies)  # scatter绘制散点图，[k] * len(accuracies)就是将[k]复制len(accuracies)份，变成[k,k,k,k,k]
 
# plot the trend line with error bars that correspond to standard deviation  用与标准偏差相对应的误差线绘制趋势线
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()

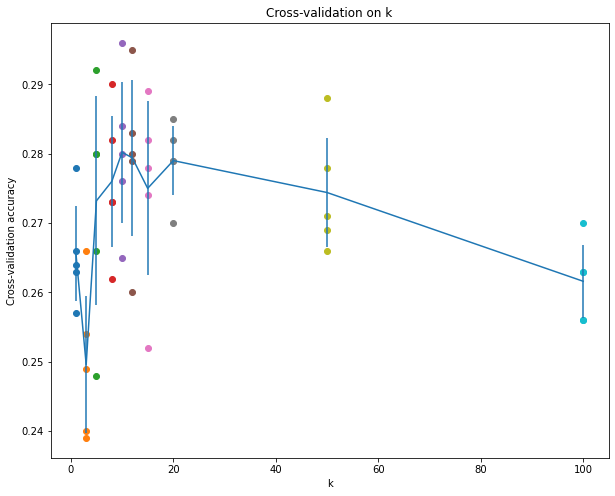
# Based on the cross-validation results above, choose the best value for k,   
# retrain the classifier using all the training data, and test it on the test
# data. You should be able to get above 28% accuracy on the test data.
best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)

# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

Got 141 / 500 correct => accuracy: 0.282000

Inline Question 3

Which of the following statements about $k$-Nearest Neighbor ($k$-NN) are true in a classification setting, and for all $k$? Select all that apply.

1. The decision boundary of the k-NN classifier is linear.
2. The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3. The test error of a 1-NN will always be lower than that of a 5-NN.
4. The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5. None of the above.

$\text{Y}ourAnswer:$
2.4

$\text{Y}ourExplanation:$

1.KNN不是线性的，看他的边界就知道，是由很多折线构成，也就是说它是局部线性的
2.这里的训练误差可以理解成将训练集记录下来之后，再拿出来部分训练集进行预测，得到的误差就是训练误差。
很明显，此时每张测试图片都能在训练集中找到与其完全相同的，所以1-NN的训练误差是0。而5-NN的误差可能是0，比如5张图片分类都是相同的，要或大于0
3.测试集误差1-NN总比5-NN小，很明显不对。测试集看的是数据的泛化能力。从前面的测试也能看出来，K属于超参数，需要调优，无法理论分析出哪个K最好
4.数据量变大，显然。

最后

以上就是含蓄冷风为你收集整理的1.knn.ipynbk-Nearest Neighbor (kNN) exercise的全部内容，希望文章能够帮你解决1.knn.ipynbk-Nearest Neighbor (kNN) exercise所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。