CS231n的assignment-1 实现（KNN部分，2022）

assignment-1作业地址如下：

https://cs231n.github.io/assignments2022/assignment1/

在导入训练集和测试集的时候遇到了：

FileNotFoundError: [Errno 2] No such file or directory: 'cs231n/datasets/cifar-10-batches-py\data_batch_1'

于是将数据集下到本地，这里我数据集在本地的相对于knn.ipynb的地址：cs231n/datasets/CIFAR10（下载数据可看：传送门）

第一个任务是完成compute_distances_two_loops部分：

Compute the distance between each test point in X and each training point in self.X_train using a nested loop over both the training data and the test data.

计算一下欧氏距离就好了，其实就是遍历X_test（500个）中的所有样本，计算每个样本与X_train（5000个）的距离，并把距离保存在dists数组中（dists数组的维度：500, 5000）：

dists[i, j] = np.sum((X[i] - self.X_train[j])**2)**0.5

一些numpy的文档可看：https://cs231n.github.io/python-numpy-tutorial/#jupyter-and-colab-notebooks

之后绘制热图（通过色差、亮度来展示数据的差异）长这样：

Inline Question 1

Notice the structured patterns in the distance matrix, where some rows or columns are visibly brighter. (Note that with the default color scheme black indicates low distances while white indicates high distances.)

• What in the data is the cause behind the distinctly bright rows?
• What causes the columns?

$\text{Y}ourAnswer:$

• 对于What in the data is the cause behind the distinctly bright rows?既然这一个测试集和其他所有的训练集差别都很大，那可能是这个测试集的特征比较诡异，或者背景颜色方面比较特殊
• 对于What causes the columns?那就说明这个训练集数据比较特殊，在所有的测试集中没有任何类似的点

之后完成predict_labels部分

在这里我对dists数组进行排序，从5000个点找到取距离最近的k个点，记为idx，之后在idx中统计每个类别的个数，即class0在idx中有几个样本，class1在idx中有几个样本等（这里一共10个class，idx个数为k）

第一个TODO为：

idx = np.argsort(dists[i])[:k]
closest_y = self.y_train[idx]

之后统计待标记样本的类别，就是在idx中样本个数最多的那个类别

第二个TODO为：

counter = np.zeros(10)

# 其实closest_y的大小就是k
for j in closest_y: 
  counter[j] += 1

# https://blog.csdn.net/t20134297/article/details/105007292/
y_pred[i] = np.argmax(counter)

也可以这么写：

counter = np.zeros(np.max(self.y_train) + 1)  # counter = np.zeros(10)

'''for j in closest_y: 
  counter[j] += 1'''
  
# https://blog.csdn.net/kingsure001/article/details/108168331
np.add.at(counter, closest_y, 1) # 按照上面的写法也可以

y_pred[i] = np.argmax(counter)

Inline Question 2

We can also use other distance metrics such as L1 distance.For pixel values $p_{ij}^{(k)}$ at location $(i,j)$ of some image $I_k$,

the mean $\mu$ across all pixels over all images is $$\mu =\frac{1}{nhw}\sum _{k=1}^n\sum _{i=1}^h\sum _{j=1}^w{p}_{ij}^{(k)}$$
And the pixel-wise mean ${\mu }_{ij}$ across all images is
$${\mu }_{ij}=\frac{1}{n}\sum _{k=1}^n{p}_{ij}^{(k)}.$$
The general standard deviation $\sigma$ and pixel-wise standard deviation ${\sigma }_{ij}$ is defined similarly.

Which of the following preprocessing steps will not change the performance of a Nearest Neighbor classifier that uses L1 distance? Select all that apply.

1. Subtracting the mean $\mu$ (${\tilde{p}}_{ij}^{(k)}=p_{ij}^{(k)}-\mu$.)
2. Subtracting the per pixel mean ${\mu }_{ij}$ (${\tilde{p}}_{ij}^{(k)}=p_{ij}^{(k)}-{\mu }_{ij}$.)
3. Subtracting the mean $\mu$ and dividing by the standard deviation $\sigma$.
4. Subtracting the pixel-wise mean ${\mu }_{ij}$ and dividing by the pixel-wise standard deviation ${\sigma }_{ij}$.
5. Rotating the coordinate axes of the data.

$\text{Y}ourAnswer:$

1，3

$\text{Y}ourExplanation:$

$L1$距离公式：$d_1\left(I_1,I_2\right)={\sum }_p\left|I_1^p-I_2^p\right|$

$L2$距离公式：$d_2\left(I_1,I_2\right)=\sqrt{{\sum }_p(I_1^p-I_2^p{)}^2}$

• 每个像素减去相同的平均值，$L1，L2$损耗值均减去相同常数项，相对损耗不变，$L1，L2$计算方式均不影响KNN性能
• 每个像素减去不同的平均值，$L1，L2$损耗值减去常数项不一定相同，$L1，L2$计算方式均影响KNN性能
• 距离缩放比相同，$L1，L2$损耗值均除以相同常数项，结果排名不变，$L1，L2$计算方式均不影响KNN性能
• 距离缩放比不同，$L1，L2$损耗值除以的常数项不一定相同，$L1，L2$计算方式均影响KNN性能
• 可以举一些简单例子证明，如点集$\{(0,0),(2,2)\}$逆时针转$45^{\circ }$后为$\{(0,0),\left(0,2\sqrt{2}\right)\}$，得出$L1$计算方式影响KNN性能，但$L2$计算方式不影响KNN性能

常用$L1$ Numpy实现：

for i in range(num_test):
  for j in range(num_train):
    a = X_test[i]-X_train[j]
    b = np.fabs(a)
    dists[i][j] = np.sum(b)

常用$L2$ Numpy实现：

for i in range(num_test):
  for j in range(num_train):
    a = X_test[i]-X_train[j]
    b = np.square(a)
    c = np.sum(b)
    dists[i][j] = np.sqrt(c)

之后完成compute_distances_one_loop部分，即实现运算的部分向量化：

dists[i] = np.sum((X[i] - self.X_train)**2, axis=1)**0.5

完成compute_distances_one_loop部分，即实现运算的完全向量化，这里直接把完全平方公式展开，用向量内积计算（dot函数可看：python中dot函数总结）：

假设 $X$ 是测试集$(m\ast d)$，训练集 $Y$ 是$(n\ast d)$，其中$m$是测试数据数量，$n$是训练数据数量，$d$是维度，计算两者公式如下：

$$\sum _{i=0}^m\sum _{j=0}^n\sqrt{{\left(p_2-c_j\right)}^2}=\sum _{i=0}^m\sum _{j=0}^n\sqrt{{\Vert p_i\Vert }^2+\left|\right|c_j{\left|\right|}^2-2\ast p_i{c}_j}$$

这里是np.sum(X**2, axis=1, keepdims=True)的结果是$(M,1)$的矩阵

设置keepidms=True，就是保持矩阵二维或者三维的特性，(结果保持其原来维数)

np.sum(self.X_train**2, axis=1)的结果是$(N,1)$的矩阵

X.dot(self.X_train.T)的结果是$(M,N)$的矩阵（$(M,d)\cdot (d,N)->(M,N)$）

dists = np.sum(X**2, axis=1, keepdims=True) + np.sum(self.X_train**2, axis=1) - 2*X.dot(self.X_train.T)
dists = dists**0.5

之后对比这3类循环的时间，发现完全向量化后的运算是最快的：

Two loop version took 60.576823 seconds
One loop version took 80.915230 seconds
No loop version took 0.343678 seconds

超参数优化

设置验证集

思路可借鉴：https://cs231n.github.io/classification/

我们将训练集一分为二：一个稍微小一点的训练集（training set），另一部分称为验证集（validation set）

以 CIFAR-10 为例，例如，我们可以使用 49，000 个训练图像进行训练，并留出 1，000 个用于验证，此验证集实质上用作假测试集来调整超参数，在此过程结束时，我们可以绘制一个图形来显示 k 的哪些值效果最好，然后，我们将一直使用此值，并在实际测试集上评估一次

交叉验证

其想法是通过设置不同的验证集并平均这些验证集的性能，可以获得更优，干扰更少的估计值 k 的工作效果，而不是任意选择前 1000 个数据点作为验证集，其他的作为训练集

例如，在 5 倍交叉验证中，我们将训练数据拆分为 5 个大小相等的部分，其中 4 个用于训练，1 个用于验证，然后，我们这 5 个部分分别设置为验证集，评估性能，最后平均这 5 个验证集的性能作为这个 k 值的工作效果

把训练集分成5份：

X_train_folds = np.array_split(X_train, num_folds)  # 分成5份
y_train_folds = np.array_split(y_train, num_folds)

之后循环5次进行训练，把每个k的结果放入对应的k_to_accuracies[k]中：

for k in k_choices:
    k_to_accuracies[k] = []
    for i in range(num_folds):
        X_train_cv = np.vstack(X_train_folds[:i] + X_train_folds[i + 1:])
        y_train_cv = np.hstack(y_train_folds[:i] + y_train_folds[i + 1:])
        X_test_cv = X_train_folds[i]
        y_test_cv = y_train_folds[i]

        classifier = KNearestNeighbor()
        classifier.train(X_train_cv, y_train_cv)
        dists = classifier.compute_distances_no_loops(X_test_cv)
        y_test_pred = classifier.predict_labels(dists, k)
        num_correct = np.sum(y_test_pred == y_test_cv)
        accuracy = float(num_correct) / X_test_cv.shape[0]
        k_to_accuracies[k].append(accuracy)

不同 k 值的结果：

k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.239000
k = 3, accuracy = 0.249000
k = 3, accuracy = 0.240000
k = 3, accuracy = 0.266000
k = 3, accuracy = 0.254000
k = 5, accuracy = 0.248000
k = 5, accuracy = 0.266000
k = 5, accuracy = 0.280000
k = 5, accuracy = 0.292000
k = 5, accuracy = 0.280000
k = 8, accuracy = 0.262000
k = 8, accuracy = 0.282000
k = 8, accuracy = 0.273000
k = 8, accuracy = 0.290000
k = 8, accuracy = 0.273000
k = 10, accuracy = 0.265000
k = 10, accuracy = 0.296000
k = 10, accuracy = 0.276000
k = 10, accuracy = 0.284000
k = 10, accuracy = 0.280000
k = 12, accuracy = 0.260000
k = 12, accuracy = 0.295000
k = 12, accuracy = 0.279000
k = 12, accuracy = 0.283000
k = 12, accuracy = 0.280000
k = 15, accuracy = 0.252000
k = 15, accuracy = 0.289000
k = 15, accuracy = 0.278000
k = 15, accuracy = 0.282000
k = 15, accuracy = 0.274000
k = 20, accuracy = 0.270000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.279000
k = 20, accuracy = 0.282000
k = 20, accuracy = 0.285000
k = 50, accuracy = 0.271000
k = 50, accuracy = 0.288000
k = 50, accuracy = 0.278000
k = 50, accuracy = 0.269000
k = 50, accuracy = 0.266000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.270000
k = 100, accuracy = 0.263000
k = 100, accuracy = 0.256000
k = 100, accuracy = 0.263000

绘制的图像：

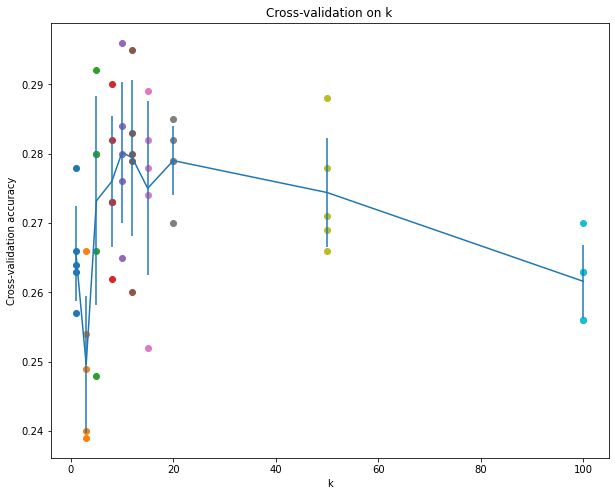
选择k = 7，测试集的正确率：

Got 137 / 500 correct => accuracy: 0.274000

选择k = 10，测试集的正确率：

Got 141 / 500 correct => accuracy: 0.282000

predict_labels函数优化（acc：27.4%->29.4%）

但是在官网说 k = 7的时候有最优解，于是想去优化predict_labels函数

链接：https://cs231n.github.io/classification/#summary-applying-knn-in-practice

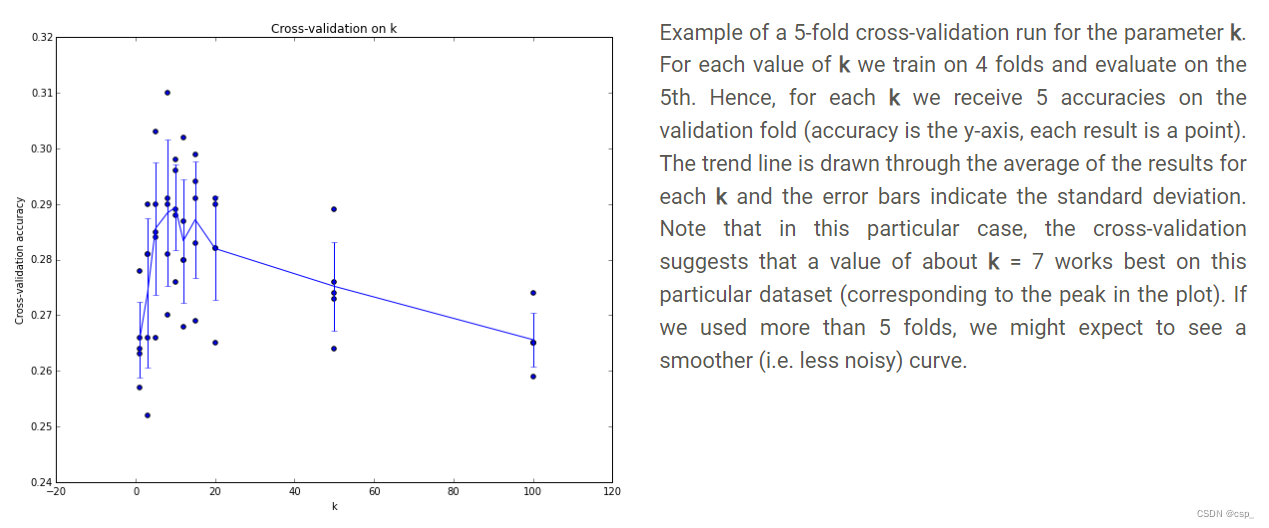
优化思路：

k数最大的类别不会重复，但可能有多个，这时是按照顺序选择的，也就是选择距离最小的那一个作为预测值，但是如果它的另一个同类距离较大，然而另一类距离均较小，这时另一类更有可能是正解，因此采取策略为：若最大类别出现重复，取这一类的均值作为评判指标

此时，predict_labels的第二个TODO改为：

counter = np.zeros(np.max(self.y_train) + 1)  # counter = np.zeros(10)

# 因为后面需要求最小值，所以bin_sum初始赋值为无穷大
bin_sum = np.zeros(np.max(self.y_train) + 1) + np.inf

# 其实closest_y的大小就是k
for j in closest_y[:k]: 
    counter[j] += 1
    
max_num=np.max(counter)

# https://www.jb51.net/article/207257.htm
# np.where()[0] 表示行索引，np.where()[1]表示列索引
class_idx=np.where(counter==max_num)[0] # 取出k数最大的类别，不会重复，但可能有多个

if len(class_idx)>1:
    dis_k=dists[i,idx] # 前k个距离
    for j in class_idx: # 将每个最大类别的欧几里得距离求总和
        idx_j=np.where(closest_y[:k]==j)[0]
        bin_sum[j]=np.sum(dis_k[idx_j])
    # 因为这里需要求最小值，所以bin_sum初始赋值为无穷大
    y_pred[i]=np.argmin(bin_sum)
else:
    y_pred[i]=class_idx[0]

此时不同 k 值的结果：

k = 1, accuracy = 0.263000
k = 1, accuracy = 0.257000
k = 1, accuracy = 0.264000
k = 1, accuracy = 0.278000
k = 1, accuracy = 0.266000
k = 3, accuracy = 0.257000
k = 3, accuracy = 0.263000
k = 3, accuracy = 0.273000
k = 3, accuracy = 0.282000
k = 3, accuracy = 0.270000
k = 5, accuracy = 0.263000
k = 5, accuracy = 0.274000
k = 5, accuracy = 0.292000
k = 5, accuracy = 0.297000
k = 5, accuracy = 0.288000
k = 8, accuracy = 0.271000
k = 8, accuracy = 0.298000
k = 8, accuracy = 0.284000
k = 8, accuracy = 0.301000
k = 8, accuracy = 0.291000
k = 10, accuracy = 0.270000
k = 10, accuracy = 0.305000
k = 10, accuracy = 0.288000
k = 10, accuracy = 0.295000
k = 10, accuracy = 0.286000
k = 12, accuracy = 0.268000
k = 12, accuracy = 0.304000
k = 12, accuracy = 0.286000
k = 12, accuracy = 0.290000
k = 12, accuracy = 0.276000
k = 15, accuracy = 0.259000
k = 15, accuracy = 0.307000
k = 15, accuracy = 0.289000
k = 15, accuracy = 0.294000
k = 15, accuracy = 0.281000
k = 20, accuracy = 0.267000
k = 20, accuracy = 0.291000
k = 20, accuracy = 0.293000
k = 20, accuracy = 0.290000
k = 20, accuracy = 0.283000
k = 50, accuracy = 0.274000
k = 50, accuracy = 0.289000
k = 50, accuracy = 0.282000
k = 50, accuracy = 0.267000
k = 50, accuracy = 0.274000
k = 100, accuracy = 0.260000
k = 100, accuracy = 0.271000
k = 100, accuracy = 0.266000
k = 100, accuracy = 0.260000
k = 100, accuracy = 0.266000
# plot the raw observations

绘制的图像：

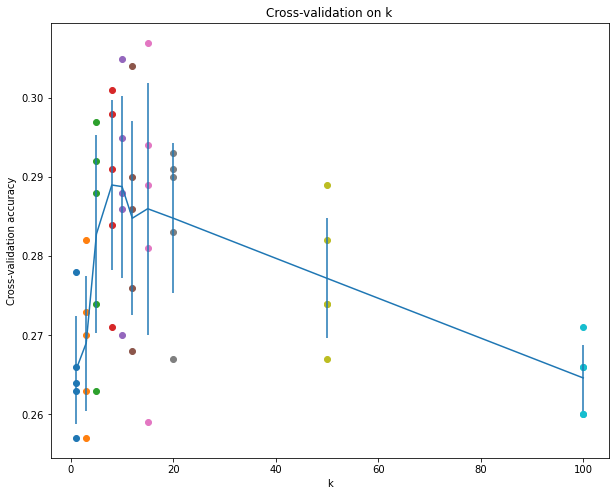
选择k = 7，测试集的正确率：

Got 148 / 500 correct => accuracy: 0.296000

选择k = 10，测试集的正确率：

Got 147 / 500 correct => accuracy: 0.294000

可以看出结果变好了

Inline Question 3

Which of the following statements about $k$-Nearest Neighbor ($k$-NN) are true in a classification setting, and for all $k$? Select all that apply.

1. The decision boundary of the k-NN classifier is linear.
2. The training error of a 1-NN will always be lower than or equal to that of 5-NN.
3. The test error of a 1-NN will always be lower than that of a 5-NN.
4. The time needed to classify a test example with the k-NN classifier grows with the size of the training set.
5. None of the above.

$\text{Y}ourAnswer:$

2，4

$\text{Y}ourExplanation:$

1. 因为输入和输出没有线性关系，所以KNN不是线性分类器，KNN的分界面由很多小的线性空间组成，分界面局部是线性的
2. 当k=1时表示只有最近的点做判断的依据，因此训练没有误差，k=5 的时候，根据vote（分类决策）的规则不同，会有不一样的训练误差
3. k越小，如果某些数据存在噪声，过拟合，则泛化能力就差，因此 k=1 不一定优于 k=5
4. 在测试中，KNN需要对整个数据集进行计算，并按距离对点进行排序，因此所需的时间随着数据的大小而增加

借鉴资料：

k-Nearest Neighbor (kNN) exercise

CS231N作业详解零基础版

Solutions to Stanford’s CS 231n Assignments 1 Inline Problems: KNN

最后

以上就是闪闪外套为你收集整理的CS231n的assignment-1 实现（KNN部分，2022）的全部内容，希望文章能够帮你解决CS231n的assignment-1 实现（KNN部分，2022）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。