3.k近邻算法
3.1 kNN算法的实现
k近邻算法(k-Nearest Neighbors)也称为kNN算法,它是算法中最简单、最基础的一种。kNN的基本思想:将数据集分为训练数据集和测试数据集,为了测试的准确率,两个数据集互异;计算测试数据集中每一个样本和训练数据集中每一个样本的距离,统计出距离值最小的k个样本(训练数据集),对k个样本中的标签值进行统计,最多的那个标签值为测试样本的预测;对测试数据集中所有的样本进行预测,并计算准确率。
3.1.1自己实现kNN算法
使用欧式距离进行计算,在n维空间中,点x和y的距离:
d(x,y) = 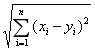
#程序3-1
import numpy as np
from sklearn import datasets
from math import sqrt
from collections import Counter
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
print(iris.keys())
np.random.seed(1)
random_index = np.random.permutation(len(iris.data))
proportion = 0.2
train_size = int((1-proportion)*len(iris.data))
train_index = random_index[:train_size]
test_index = random_index[train_size:]
#训练数据集
#或train_X = iris.data[train_index]不写列,只对行进行fancy indexing
X_train = iris.data[train_index,:]
y_train = iris.target[train_index]
#测试数据集
X_test = iris.data[test_index,:]
y_test = iris.target[test_index]
print('X_train:n',X_train.shape)
print('y_train:n',y_train.shape)
def distance(k,X_train,y_train,x):
#计算x到训练集X_train中每一个点的距离,索引排序后;
# 通过索引值取出y_train中的k个元素
# 对k个元素进行计数,返回计数最多值对应的target
distances = []
for x_train in X_train:
dist = sqrt(sum((x_train - x)**2))
distances.append(dist)
distances_arg = np.argsort(distances)
topK_y = [y_train[top_arg] for top_arg in distances_arg[:k]]
top_counter = Counter(topK_y)
top_most = top_counter.most_common(1)
return top_most[0][0]
y_predict = []
for x_test in X_test:
#对X_test中的每个元素求距离,将返回的target存入y_predict中
y_dis = distance(8,X_train,y_train,x_test)
y_predict.append(y_dis)
accuracy_rate = sum(y_predict==y_test)/len(y_test)
print('预测准确率: ',accuracy_rate)
运行结果:
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
X_train:
(120, 4)
y_train:
(120,)
预测准确率: 0.9666666666666667
3.1.2使用sklearn库封装的kNN
官方文档:https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier.fit
#程序3-2
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
print(iris.keys())
#train_size表示训练数据集所占比例
#test_size表示测试数据集所占比例
#train_size + test_size = 1,尽量使用test_size
#random_state表示随机种子
#相当于X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,
# train_size=0.8,random_state=123)
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,
test_size=0.2,random_state=123)
print('X_train:n',X_train.shape)
print('X_test:n',X_test.shape)
print('y_train:n',y_train.shape)
print('y_test:n',y_test.shape)
iris_kNNClassifier = KNeighborsClassifier(n_neighbors=8)
#训练数据集使用kNN算法进行训练,得到模型
iris_kNNClassifier.fit(X_train,y_train)
#使用模型对测试数据集进行预测
# y_predict = iris_kNNClassifier.predict(X_test)
# accuracy_rate = accuracy_score(y_test,y_predict)
accuracy_rate = iris_kNNClassifier.score(X_test,y_test)
print('预测准确率: ',accuracy_rate)
运行结果:
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
X_train:
(120, 4)
X_test:
(30, 4)
y_train:
(120,)
y_test:
(30,)
预测准确率: 0.9666666666666667
3.2超参数
对于同一个学习算法,当使用不同的参数配置时,也会产生不同的模型。因此,在使用学习算法时,如何调参是很重要的问题。
超参数是在算法运行前需要决定的参数;在kNN算法中,超参数有k、距离的权重、明可夫斯基距离参数p。模型参数是在算法过程中学习的参数;kNN算法中并没有模型参数。
3.2.1超参数k
当选取k为何值时,准确率最高?
#程序3-3
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
best_k = -1
best_score = 0.0
for k in range(1,11):
iris_kNNClassifier = KNeighborsClassifier(n_neighbors=k)
iris_kNNClassifier.fit(X_train,y_train)
score = iris_kNNClassifier.score(X_test,y_test)
if score > best_score:
best_score = score
best_k = k
print('k = %d 时准确率最高,score = %f'%(best_k,best_score))
运行结果:
k = 5 时准确率最高,score = 0.977778
3.2.2距离的权重
在训练数据集中有4个训练样本和测试样本最近,setosa有1个训练样本,距离为1,versicolor有2个训练样本,距离为4、5,virginica有1个训练样本,距离为3。
若考虑距离的权重,则setosa的权重是1,versicolor的权重是1/4 + 1/5 = 9/20,virginica的权重是1/3。因为setosa最大,所以预测结果是setosa。
在官方文档https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier中,KNeighborsClassifier的weights参数默认是uniform,即不考虑距离权重;若将weights设置为distance,则表示考虑距离权重。
#程序3-4
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
weights = ['uniform','distance']
best_weight = ''
best_k = -1
best_score = 0.0
for weight in weights:
for k in range(1,10):
iris_kNNClassifier = KNeighborsClassifier(n_neighbors=k,weights=weight)
iris_kNNClassifier.fit(X_train,y_train)
score = iris_kNNClassifier.score(X_test,y_test)
if score > best_score:
best_score = score
best_k = k
best_weight = weight
print('best_weight:%s,best_k:%d,best_score:%f'%(best_weight,best_k,best_score))
运行结果:
best_weight:uniform,best_k:5,best_score:0.977778
使用for循环进行最好参数的搜索非常麻烦,在sklearn.model_selection中提供了网格搜索的办法。官方文档:https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV。
#程序3-5
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split,GridSearchCV
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
print(X_train.shape)
print(y_train.shape)
kNN_Classifier = KNeighborsClassifier()
#kNN_grid = [
# {
# 'weights': ['uniform','distance'],
# 'n_neighbors': [i for i in range(1, 11)]
# }
# ]
kNN_grid = {
'weights': ['uniform','distance'],
'n_neighbors': [i for i in range(1, 11)]
}
kNN_grid_search = GridSearchCV(kNN_Classifier,kNN_grid,n_jobs=-1,iid='True',cv=3,verbose=2)
#训练数据集
kNN_grid_search.fit(X_train,y_train)
#最优参数的分类器
print('best_estimator_:',kNN_grid_search.best_estimator_)
#成员提供优化过程期间观察到的最高准确率
print('best_score_:',kNN_grid_search.best_score_)
#网格搜索中的最优参数值
print('best_params_:',kNN_grid_search.best_params_)
#预测测试数据集
iris_kNN = kNN_grid_search.best_estimator_
y_predict = iris_kNN.predict(X_test)
score = iris_kNN.score(X_test,y_test)
print('准确率:',score)
运行结果:
(105, 4)
(105,)
Fitting 3 folds for each of 20 candidates, totalling 60 fits
[Parallel(n_jobs=-1)]: Using backend LokyBackend with 8 concurrent workers.
[CV] n_neighbors=1, weights=uniform ..................................
[CV] ................... n_neighbors=1, weights=uniform, total= 0.0s
[CV] n_neighbors=2, weights=uniform ..................................
[CV] n_neighbors=1, weights=uniform ..................................
[CV] n_neighbors=1, weights=uniform ..................................
[CV] n_neighbors=1, weights=distance .................................
[CV] ................... n_neighbors=2, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=1, weights=distance, total= 0.0s
[CV] ................... n_neighbors=1, weights=uniform, total= 0.0s
[CV] ................... n_neighbors=1, weights=uniform, total= 0.0s
[CV] n_neighbors=2, weights=distance .................................
[CV] n_neighbors=2, weights=distance .................................
[CV] n_neighbors=2, weights=distance .................................
[CV] .................. n_neighbors=2, weights=distance, total= 0.0s
[CV] n_neighbors=1, weights=distance .................................
[CV] .................. n_neighbors=2, weights=distance, total= 0.0s
[CV] n_neighbors=3, weights=uniform ..................................
[CV] .................. n_neighbors=2, weights=distance, total= 0.0s
[CV] n_neighbors=3, weights=uniform ..................................
[CV] n_neighbors=1, weights=distance .................................
[CV] .................. n_neighbors=1, weights=distance, total= 0.0s
[CV] .................. n_neighbors=1, weights=distance, total= 0.0s
[CV] ................... n_neighbors=3, weights=uniform, total= 0.0s
[CV] n_neighbors=3, weights=uniform ..................................
[CV] n_neighbors=3, weights=distance .................................
[CV] .................. n_neighbors=3, weights=distance, total= 0.0s
[CV] n_neighbors=3, weights=distance .................................
[CV] ................... n_neighbors=3, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=3, weights=distance, total= 0.0s
[CV] n_neighbors=2, weights=uniform ..................................
[CV] n_neighbors=3, weights=distance .................................
[CV] n_neighbors=4, weights=uniform ..................................
[CV] n_neighbors=4, weights=uniform ..................................
[CV] n_neighbors=4, weights=uniform ..................................
[CV] n_neighbors=4, weights=distance .................................
[CV] .................. n_neighbors=3, weights=distance, total= 0.0s
[CV] ................... n_neighbors=3, weights=uniform, total= 0.0s
[CV] n_neighbors=4, weights=distance .................................
[CV] n_neighbors=4, weights=distance .................................
[CV] .................. n_neighbors=4, weights=distance, total= 0.0s
[CV] n_neighbors=5, weights=uniform ..................................
[CV] .................. n_neighbors=4, weights=distance, total= 0.0s
[CV] n_neighbors=5, weights=uniform ..................................
[CV] .................. n_neighbors=4, weights=distance, total= 0.0s
[CV] ................... n_neighbors=4, weights=uniform, total= 0.0s
[CV] n_neighbors=5, weights=uniform ..................................
[CV] ................... n_neighbors=4, weights=uniform, total= 0.0s
[CV] ................... n_neighbors=2, weights=uniform, total= 0.0s
[CV] ................... n_neighbors=5, weights=uniform, total= 0.0s
[CV] n_neighbors=5, weights=distance .................................
[CV] ................... n_neighbors=5, weights=uniform, total= 0.0s
[CV] n_neighbors=5, weights=distance .................................
[CV] n_neighbors=5, weights=distance .................................
[CV] ................... n_neighbors=4, weights=uniform, total= 0.0s
[CV] n_neighbors=6, weights=uniform ..................................
[CV] .................. n_neighbors=5, weights=distance, total= 0.0s
[CV] .................. n_neighbors=5, weights=distance, total= 0.0s
[CV] n_neighbors=6, weights=uniform ..................................
[CV] .................. n_neighbors=5, weights=distance, total= 0.0s
[CV] n_neighbors=6, weights=uniform ..................................
[CV] n_neighbors=6, weights=distance .................................
[CV] ................... n_neighbors=5, weights=uniform, total= 0.0s
[CV] n_neighbors=6, weights=distance .................................
[CV] ................... n_neighbors=6, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=6, weights=distance, total= 0.0s
[CV] n_neighbors=6, weights=distance .................................
[CV] ................... n_neighbors=6, weights=uniform, total= 0.0s
[CV] ................... n_neighbors=6, weights=uniform, total= 0.0s
[CV] n_neighbors=7, weights=uniform ..................................
[CV] .................. n_neighbors=6, weights=distance, total= 0.0s
[CV] .................. n_neighbors=6, weights=distance, total= 0.0s
[CV] n_neighbors=7, weights=uniform ..................................
[CV] n_neighbors=7, weights=uniform ..................................
[CV] ................... n_neighbors=7, weights=uniform, total= 0.0s
[CV] n_neighbors=7, weights=distance .................................
[Parallel(n_jobs=-1)]: Done 25 tasks | elapsed: 1.2s
[CV] ................... n_neighbors=7, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=7, weights=distance, total= 0.0s
[CV] n_neighbors=7, weights=distance .................................
[CV] ................... n_neighbors=7, weights=uniform, total= 0.0s
[CV] n_neighbors=7, weights=distance .................................
[CV] .................. n_neighbors=7, weights=distance, total= 0.0s
[CV] .................. n_neighbors=7, weights=distance, total= 0.0s
[CV] n_neighbors=8, weights=uniform ..................................
[CV] n_neighbors=8, weights=uniform ..................................
[CV] n_neighbors=8, weights=distance .................................
[CV] ................... n_neighbors=8, weights=uniform, total= 0.0s
[CV] n_neighbors=9, weights=uniform ..................................
[CV] n_neighbors=2, weights=uniform ..................................
[CV] ................... n_neighbors=8, weights=uniform, total= 0.0s
[CV] n_neighbors=9, weights=uniform ..................................
[CV] n_neighbors=9, weights=distance .................................
[CV] n_neighbors=8, weights=uniform ..................................
[CV] n_neighbors=8, weights=distance .................................
[CV] .................. n_neighbors=8, weights=distance, total= 0.0s
[CV] n_neighbors=8, weights=distance .................................
[CV] .................. n_neighbors=8, weights=distance, total= 0.0s
[CV] ................... n_neighbors=9, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=9, weights=distance, total= 0.0s
[CV] ................... n_neighbors=8, weights=uniform, total= 0.0s
[CV] ................... n_neighbors=9, weights=uniform, total= 0.0s
[CV] n_neighbors=9, weights=distance .................................
[CV] n_neighbors=9, weights=distance .................................
[CV] n_neighbors=9, weights=uniform ..................................
[CV] ................... n_neighbors=2, weights=uniform, total= 0.0s
[CV] .................. n_neighbors=8, weights=distance, total= 0.0s
[CV] .................. n_neighbors=9, weights=distance, total= 0.0s
[CV] .................. n_neighbors=9, weights=distance, total= 0.0s
[CV] n_neighbors=10, weights=uniform .................................
[CV] n_neighbors=10, weights=uniform .................................
[CV] n_neighbors=10, weights=distance ................................
[CV] ................... n_neighbors=9, weights=uniform, total= 0.0s
[Parallel(n_jobs=-1)]: Done 45 out of 60 | elapsed: 1.2s remaining: 0.3s
[CV] ................. n_neighbors=10, weights=distance, total= 0.0s
[CV] n_neighbors=10, weights=distance ................................
[CV] .................. n_neighbors=10, weights=uniform, total= 0.0s
[CV] n_neighbors=10, weights=uniform .................................
[CV] .................. n_neighbors=10, weights=uniform, total= 0.0s
[CV] n_neighbors=10, weights=distance ................................
[CV] ................. n_neighbors=10, weights=distance, total= 0.0s
[CV] ................. n_neighbors=10, weights=distance, total= 0.0s
[CV] .................. n_neighbors=10, weights=uniform, total= 0.0s
[Parallel(n_jobs=-1)]: Done 60 out of 60 | elapsed: 1.2s finished
best_estimator_: KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=6, p=2,
weights='distance')
best_score_: 0.9714285714285714
best_params_: {'n_neighbors': 6, 'weights': 'distance'}
准确率: 0.9777777777777777
为什么只使用训练数据集就可以得到best_score_?
因为函数GridSearchCV表示使用交叉验证。k折交叉验证将样本随机均匀的分为k份,轮流用k-1分训练模型,1份用于测试模型准确率,用k个准确率的均值作为最终的准确率。
函数原型:GridSearchCV(estimator, param_grid, scoring=None, fit_params=None, n_jobs=None, iid=’warn’, refit=True, cv=’warn’, verbose=0, pre_dispatch=’2*n_jobs’, error_score=’raise-deprecating’, return_train_score=’warn’)
参数estimator:所使用的分类器,如estimator=RandomForestClassifier(min_samples_split=100,min_samples_leaf=20,max_depth=8,max_features='sqrt',random_state=10),并且传入除需要确定最佳的参数之外的其他参数。每一个分类器都需要一个scoring参数,或者score方法。
参数param_grid:值为字典或元素为字典的列表,即需要最优化参数的取值。
参数scoring:准确度评价标准,默认None,需要使用score函数;或scoring='roc_auc',根据所选模型不同,评价准则不同。
参数cv:交叉验证参数,默认None,即使用三折交叉验证(指定fold数量为3)。
参数refit:默认为True,程序在搜索参数结束后,用最佳参数再次fit一遍全部数据集。
参数iid:默认True,表示各个样本fold概率分布一致,误差估计为所有样本之和,而非各个fold的平均。
参数verbose:日志冗长度(int),冗长度为0表示不输出训练过程;1表示偶尔输出;>1表示对每个子模型都输出。
参数n_jobs:并行数(int),默认为1,表示使用一个CPU核,-1表示使用所有的CPU核。
参考博客:https://blog.csdn.net/u012969412/article/details/72973055
3.2.3明可夫斯基距离参数p
在n维空间中,求取点a和b的距离,点a坐标(a1,a2,...,an),点b坐标(b1,b2,...,bn)。
曼哈顿距离:d(a,b) = ![]()
欧拉距离:d(a,b) = 
明可夫斯基距离:d(a,b) = 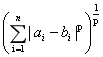
在KNeighborsClassifier中,参数p表示的就是明可夫斯基距离中的p,因此p也是超参数。由于只有当考虑距离时,即当weights=distance时,p才有意义。
#程序3-6
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split,GridSearchCV
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
kNN_Classifier = KNeighborsClassifier()
kNN_grid = [
{
'weights': ['uniform'],
'n_neighbors': [i for i in range(1, 11)]
},
{
'weights': ['distance'],
'n_neighbors': [i for i in range(1, 11)],
'p': [i for i in range(1, 7)]
}
]
kNN_grid_search = GridSearchCV(kNN_Classifier,kNN_grid,n_jobs=-1,iid='True',cv=3,verbose=0)
#训练数据集
kNN_grid_search.fit(X_train,y_train)
#最优参数的分类器
print('best_estimator_:',kNN_grid_search.best_estimator_)
#成员提供优化过程期间观察到的最高准确率
print('best_score_:',kNN_grid_search.best_score_)
#网格搜索中的最优参数值
print('best_params_:',kNN_grid_search.best_params_)
#预测测试数据集
iris_kNN = kNN_grid_search.best_estimator_
y_predict = iris_kNN.predict(X_test)
score = iris_kNN.score(X_test,y_test)
print('准确率:',score)
运行结果:
best_estimator_: KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=6, p=2,
weights='distance')
best_score_: 0.9714285714285714
best_params_: {'n_neighbors': 6, 'p': 2, 'weights': 'distance'}
准确率: 0.9777777777777777
3.3数据归一化
在机器学习领域,特征向量中的不同特征由于具有不同的量纲和量纲单位,会影响到数据分析的结果。因此,为了消除量纲不同带来的影响,需要对数据进行标准化处理,最典型的就是数据归一化。
在kNN算法中,需要求取样本之间的距离,以欧拉距离为例。对样本特征值差的平方求和,而不同特征值之间由于量纲的不同,因此需要对数据进行归一化处理。
数据归一化的目的是将所有的数据映射到同一尺度,常用方法最值归一化和均值方差归一化。
最值归一化是把所有的数据映射到0-1之间,公式为
![]()
最值归一化使用于有明显边界的数据集,如学生的分数;不适用于没有边界的数据集,如房价。
均值方差归一化是把所有数据归一到均值为0方差为1的分布中,公式为
![]()
其中,xmean为均值,s为方差。均值方差归一化使用于没有边界的数据集,或存在极端值的数据集;当时有边界的数据集使用均值方差归一化也是非常好的。
3.3.1自己实现数据归一化
#程序3-7:最值归一化
import numpy as np
X = np.random.randint(0,100,(20,2))
X = np.array(X,dtype=float)
col = X.shape[1]
i = 0
while i < col:
#最值归一化
X[:,i] = (X[:,i]-np.min(X[:,i]))/(np.max(X[:,i])-np.min(X[:,i]))
i += 1
print(X)
运行结果:
[[0.37209302 0. ]
[1. 0.38461538]
[0.48837209 1. ]
[0.1744186 0.59340659]
[0.61627907 0.96703297]
[0.55813953 0.49450549]
[0.77906977 0.93406593]
[0.97674419 0.52747253]
[0.43023256 0.87912088]
[0.18604651 0.1978022 ]
[0.45348837 0.8021978 ]
[0.89534884 0.36263736]
[0.61627907 0.56043956]
[0.05813953 0.35164835]
[1. 0.87912088]
[0.8255814 0.96703297]
[0.68604651 0.9010989 ]
[0. 0.68131868]
[0.24418605 0.7032967 ]
[0.90697674 0.28571429]]
#程序3-8:均值方差归一化
import numpy as np
X = np.random.randint(0,100,(20,2))
X = np.array(X,dtype=float)
col = X.shape[1]
i = 0
while i < col:
#均值方差归一化
X[:,i] = (X[:,i]-np.mean(X[:,i]))/np.std(X[:,i])
print('特征的均值:',np.mean(X[:,i]))
print('特征的方差:',np.std(X[:,i]))
i += 1
print(X)
运行结果:
特征的均值: -2.2204460492503132e-17
特征的方差: 1.0
特征的均值: 6.938893903907228e-17
特征的方差: 1.0
[[-0.83151186 2.08977336]
[-0.90197897 0.91751646]
[ 0.01409342 0.06086719]
[-1.50094937 -0.52526126]
[-0.76104475 1.05277687]
[-0.76104475 1.27821089]
[-0.05637369 0.01578038]
[-1.21908095 0.51173522]
[ 1.388202 -0.11948003]
[ 1.63483688 -0.20965364]
[ 1.03586647 0.01578038]
[ 0.29596185 -0.39000085]
[ 1.24726779 -1.51717095]
[ 0.47212962 -0.34491405]
[ 0.47212962 0.46664842]
[ 0.26072829 -0.48017446]
[ 1.8462382 -1.87786538]
[-1.00767963 1.27821089]
[-0.90197897 -1.74260497]
[-0.7258112 -0.48017446]]
3.3.2使用sklearn中的preprocessing
#程序3-9
import numpy as np
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:Program Files (x86)Pythonlibsite-packagessklearndatasetsdatairis.csv
'''
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=123)
stdScale = StandardScaler()
#使用训练数据集对StandardScaler对象进行训练,求的对应的均值和方差
stdScale.fit(X_train)
print('训练数据集的均值:',stdScale.mean_)
print('训练数据集的方差:',stdScale.scale_)
#对训练数据集和测试数据集进行转换,其使用的均值和方差都是训练数据集的均值、方差
X_train_std = stdScale.transform(X_train)
X_test_std = stdScale.transform(X_test)
kNN_Classifier = KNeighborsClassifier()
kNN_grid = [
{
'weights': ['uniform'],
'n_neighbors': [i for i in range(1, 11)]
},
{
'weights': ['distance'],
'n_neighbors': [i for i in range(1, 11)],
'p': [i for i in range(1, 7)]
}
]
kNN_grid_search = GridSearchCV(kNN_Classifier,kNN_grid,n_jobs=-1,iid='True',cv=3,verbose=0)
#训练数据集
kNN_grid_search.fit(X_train_std,y_train)
#最优参数的分类器
print('best_estimator_:',kNN_grid_search.best_estimator_)
#成员提供优化过程期间观察到的最高准确率
print('best_score_:',kNN_grid_search.best_score_)
#网格搜索中的最优参数值
print('best_params_:',kNN_grid_search.best_params_)
#预测测试数据集
iris_kNN = kNN_grid_search.best_estimator_
y_predict = iris_kNN.predict(X_test_std)
score = iris_kNN.score(X_test_std,y_test)
print('准确率:',score)
运行结果:
训练数据集的均值: [5.86952381 3.05047619 3.83714286 1.23238095]
训练数据集的方差: [0.792239 0.40710916 1.70608196 0.73568824]
best_estimator_: KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
best_score_: 0.9714285714285714
best_params_: {'n_neighbors': 5, 'weights': 'uniform'}
准确率: 0.9333333333333333
使用sklearn库的preprocessing模块中的类StandardScaler进行数据集的转换。
3.4评价kNN算法
优点:kNN算法适合解决多分类的任务,其实现简单、效果强大;除了分类任务,kNN算法还可以解决回归任务。
缺点:效率低下。当数据集有上万个特征,上百万个样本时,使用kNN算法是明显不合适的。
最后
以上就是优雅大炮最近收集整理的关于机器学习—k近邻算法3.k近邻算法的全部内容,更多相关机器学习—k近邻算法3内容请搜索靠谱客的其他文章。








发表评论 取消回复