前面提到的对极几何约束和单应矩阵可以求出相机的运动,然后接下来我们可以通过三角测量来获取空间地图点的深度(如下图)。
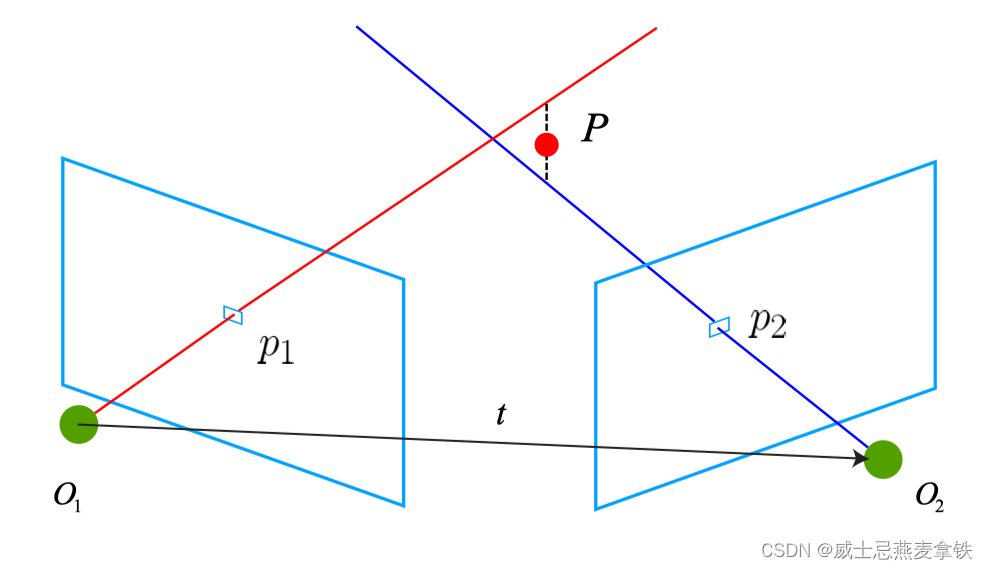
现在有图像 I 1 I_1 I1 和 I 2 I_2 I2 ,对应的相机光心分别为 O 1 O_1 O1 和 O 2 O_2 O2。在 I 1 I_1 I1 中有特征点 p 1 p_1 p1, I 2 I_2 I2 中有特征点 p 2 p_2 p2, p 1 p_1 p1 和 p 2 p_2 p2 是相匹配的特征点。
理想情况下,直线 O 1 p 1 O_1p_1 O1p1 与 O 2 p 2 O_2p_2 O2p2 会相交于一点 P boldsymbol{P} P,该点即是两个特征点所对应的地图点在三维场景中的位置。然而 由于噪声的影响,这两条直线往往无法相交。因此,通常通过最二小乘去求解。
按照对极几何中的定义,假设 x 1 boldsymbol{x}_{1} x1 和 x 2 boldsymbol{x}_{2} x2 是两个特征点的归一化坐标,那么它们满足:
s 1 x 1 = s 2 R x 2 + t (1) s_{1} boldsymbol{x}_{1}=s_{2} boldsymbol{R} boldsymbol{x}_{2}+boldsymbol{t} tag{1} s1x1=s2Rx2+t(1)
现在 R boldsymbol{R} R 和 t boldsymbol{t} t 已知,我们要求的是两个特征点 p 1 p_1 p1 和 p 2 p_2 p2 的深度 s 1 s_1 s1 和 s 2 s_2 s2。
对(1)式左乘一个 x 1 ∧ boldsymbol{x}_{1}^{wedge} x1∧ ,则有:
s 1 x 1 ∧ x 1 = 0 = s 2 x 1 ∧ R x 2 + x 1 ∧ t (2) s_{1} boldsymbol{x}_{1}^{wedge} boldsymbol{x}_{1}=0=s_{2} boldsymbol{x}_{1}^{wedge} boldsymbol{R} boldsymbol{x}_{2}+boldsymbol{x}_{1}^{wedge} boldsymbol{t} tag{2} s1x1∧x1=0=s2x1∧Rx2+x1∧t(2)
该式左侧为零,右侧是一个只包含未知量 s 2 s_2 s2 的一个方程,可以根据它直接求得 s 2 s_2 s2 ,然后再代入到(1)式中可以求出 s 1 s_1 s1 。
当然, 由于噪声的存在,我们估得的 R boldsymbol{R} R 和 t boldsymbol{t} t , 不一定精确使(2)式为零(两条直线往往无法相交)。所以更常见的做法求最小二乘解而不是零解。
关于三角测量的讨论
三角测量是由平移得到的,有平移才会有对极几何中的三角形,才谈得上三角测量。因 此,纯旋转是无法使用三角测量的,因为对极约束将永远满足。
在平移存在的情况下,我 们还要关心三角测量的不确定性,这会引出一个三角测量的矛盾。
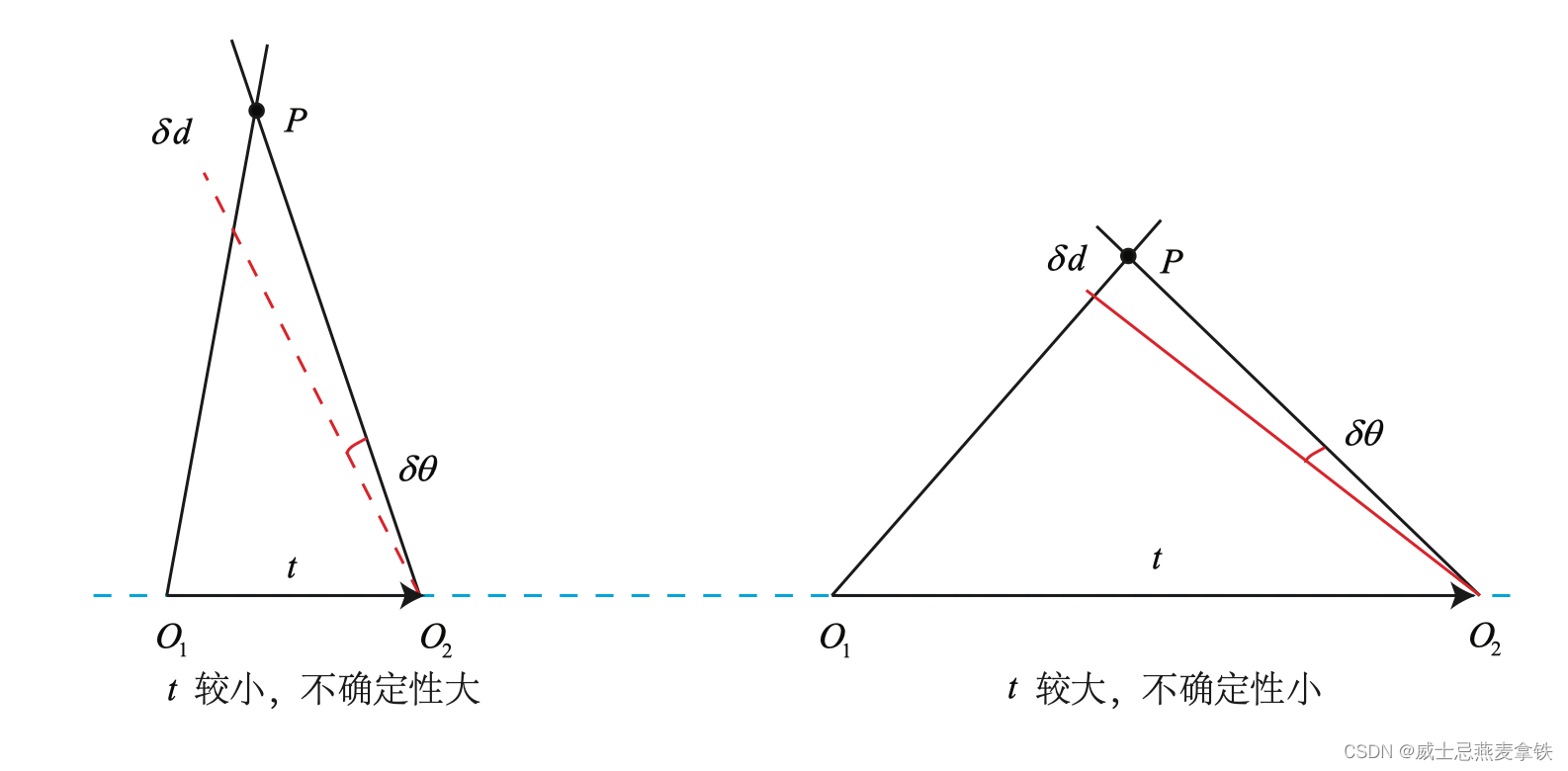
如上图所示。当平移很小时,像素上的不确定性将导致较大的深度不确定性。也就是说,如果特征点运动一个像素 δ x delta x δx, 使得视线角变化了一个角度 δ θ delta theta δθ, 那么测量到深度值将有 δ d delta d δd 的变化。从几何关系可以看到,当 t 较大时, δ d delta d δd 将明显变小,这说明平移较大时, 在同样的相机分辨率下,三角化测量将更精确。
因此,要增加三角化的精度,有两种方法:
- 提高特征点的提取精度,也就是提高图像分辨率。但这会导致图像变大,提高计算成本。
- 另一方式是使平移量增大。但是,平移量增大,会导致图像的外观发生明显的变化,比如箱子原先被挡住的侧面显示出来了,比如反射光 发生变化了,等等。外观变化会使得特征提取与匹配变得困难。
总而言之,在增大平移,会导致匹配失效;而平移太小,则三角化精度不够——这就是三角化的矛盾。
最后
以上就是调皮玉米最近收集整理的关于三角测量获取特征点深度关于三角测量的讨论的全部内容,更多相关三角测量获取特征点深度关于三角测量内容请搜索靠谱客的其他文章。








发表评论 取消回复