最近想做一个关于移动机器人的总结，就先从移动机器人的底盘说起吧。现在移动机器人这么火热，大到无人驾驶车，规矩的有工业上应用得很多的AGV（比如智能物流自动搬运机器人），小到淘宝上面的智能小车，都可以算作移动机器人。移动机器人有各种各样的底盘，有两轮的三轮的四轮的，比如无人车是四轮的阿克曼模型，一般的AGV是两轮差速模型，还有大学生机器人竞赛里面常见的三轮全向轮底盘，四轮全向轮底盘，还有一些AGV是四轮滑移底盘，是不是有点让人眼花缭乱的感觉呢，哈哈，下面就逐一来分析一下，关于运动学的话我不会推导公式，我本人也是不太喜欢推公式的，我觉得有现成的用，理解其含义就好了，我就从工程应用上面说说怎么用。

两轮差速底盘（Differential Drive robot）

就是类似下面这货,两个驱动轮，带一个万向轮，靠差速转弯，有点像两轮平衡车，但和平衡车不同的是，他三个轮子在平面上已经平衡了，不需要考虑自平衡的问题。

两轮差速底盘估计是现在应用得最多的机器人底盘了，ROS自带的DWA路径规划算法特别适合这货，他本身也可以原地旋转，还是很灵活的，简单有效，所以应用很多。

想要做全自主移动的机器人，就不能不知道自己的位置，要估计机器人的位置，就要用到里程计了，里程计有几种，轮式里程计，激光里程计，视觉里程计。 轮式里程计就是把机器人在这个很小的路程里的运动可以看成直线运动。然后就是这里实际上是对速度做一个积分，

正运动学模型（forward kinematic model）将得到一系列公式，让我们可以通过四个轮子的速度，计算出底盘的运动状态；而逆运动学模型（inverse kinematic model）得到的公式则是可以根据底盘的运动状态解算出四个轮子的速度。

我们的速度是由嵌入式设备测试来的很短时间内的一个速度，

，

上式中，input是在 时间内轮子编码器增加的读数，ppr是编码器的线数，r是轮子半径。式中的分子 实际上是在算 内轮子的平均线速度，但这只是其中一个轮子的速度，车子中心的速度实际是 左轮的速度加右轮的速度/2，即

这个速度的估计精度和编码器的精度有很大关系，而且轮子不能打滑空转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167

 
 

   
   

    
    

   
   
   
   

    
    

     
         
     
     //compute odometry in a typical way given the velocities of the robot
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         
     
     double dt = (current_time - last_time).toSec();
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         
     
     double delta_x = (vx * 
     
     cos(th) - vy * 
     
     sin(th)) * dt;
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         
     
     double delta_y = (vx * 
     
     sin(th) + vy * 
     
     cos(th)) * dt;
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         
     
     double delta_th = vth * dt;
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
        
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         x += delta_x;
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         y += delta_y;
    
    
   
   

   
   

    
    

   
   
   
   

    
    

     
         th += delta_th;
    
    
   
   
 
 

三轮全向轮底盘（Three-wheel omnidirectional wheel robot）

图片来自百度图片～，三个全向轮分别相隔120°，可以全方位移动。

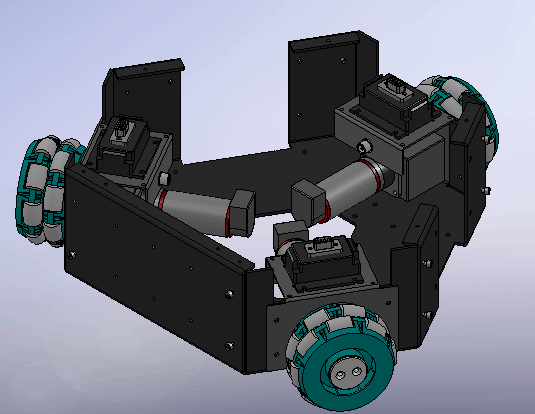
我们先以小车自身中心建立坐标系，如下图：

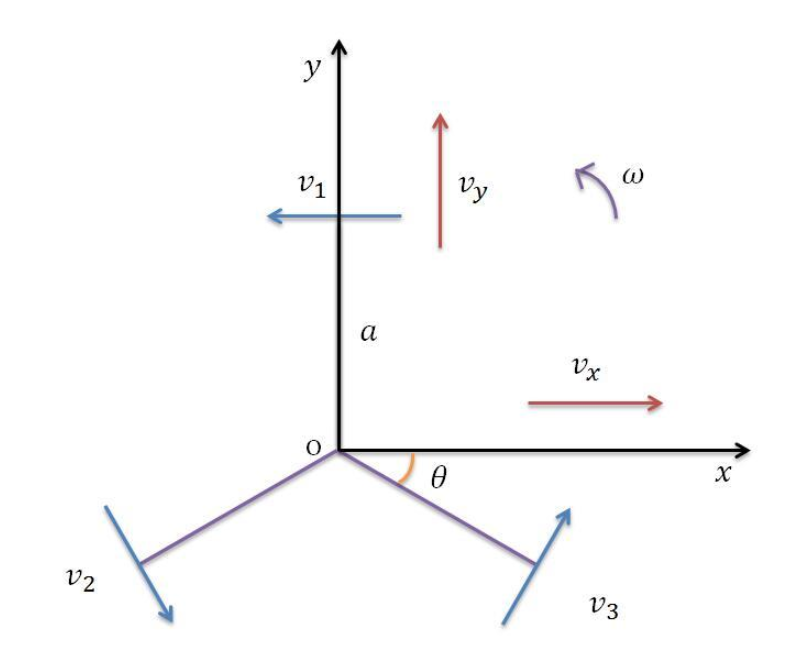
其中v_1、v_2、v_3分别为三个轮子的转速，ω为旋转角速度，v_x、v_y为车身坐标系中的速度即相对速度（由于底盘速度性能与在世界坐标系中的姿态无关，因此此处为简化运算，取车身坐标系与世界坐标系X,Y方向重合），a为旋转中心到轮轴心的垂直距离，θ为轮轴与x轴夹角，θ=π/6。不难得出各轮速度的转换矩阵为：

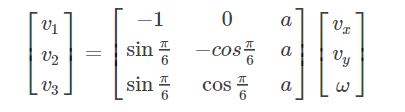
然后求逆得：

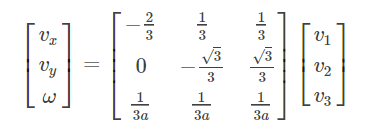
现在我们就可以根据三个轮子的轮速来确定

四轮全向轮底盘（Four-wheel omnidirectional wheel robot）

每个轮子相互垂直，成十字形摆放的时候刚好是个坐标系，不过为了性能更好，一般用X型，如下图

四轮麦克纳姆轮底盘（Four-wheeled Mecanum wheel  robot）

这个轮子也非常出名，Robomaster 就是用的这种轮子，可以像正常车轮子那样摆放，如下图

下面来分析下它的运动学

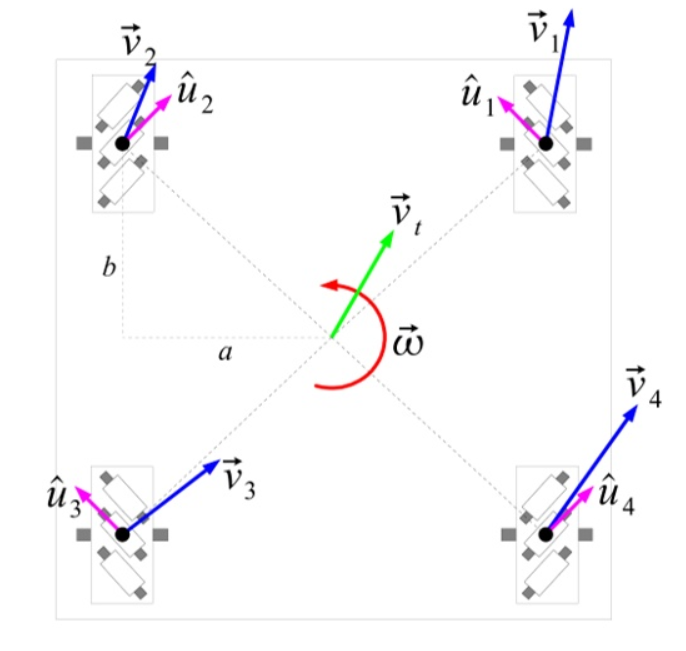
我就直接给公式了：

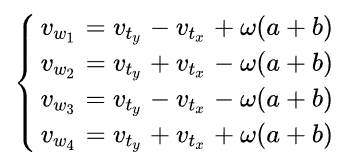
四轮滑移底盘（Four-wheel sliding robot）

这个也可以叫四轮差速底盘，他和两轮的原理一样，都是靠左右两边的速度不一样还转向，但是因为他四个轮子都是固定的，想象一下，当车子差速原地转向的时候，四个轮子就必定会有一点漂移的情况出现，就是轮子会出现侧向滑动，而两轮不会出现这种情况，因为两轮的车轴经过旋转中心。下图出名的 husky robot 就是这类底盘。

四轮阿克曼底盘（Four-wheeled Ackerman robot）

像汽车一样，前轮转向，后轮驱动的模型就叫阿克曼模型，如下图

下面来看一下运动学模型：

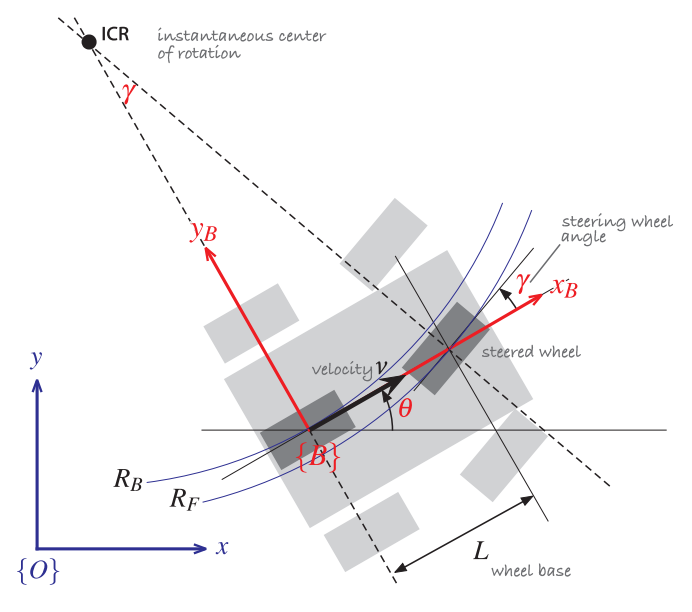
公式：

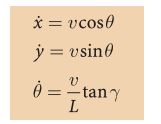
最后

以上就是跳跃煎饼最近收集整理的关于[学习SLAM]分析总结常见的几种移动机器人底盘类型及其运动学 两轮差速底盘（Differential Drive robot）三轮全向轮底盘（Three-wheel omnidirectional wheel robot）四轮全向轮底盘（Four-wheel omnidirectional wheel robot）四轮麦克纳姆轮底盘（Four-wheeled Mecanum wheel  robot）四轮滑移底盘（Four-wheel sliding robot）四轮阿克曼底盘（Four-wh的全部内容，更多相关[学习SLAM]分析总结常见的几种移动机器人底盘类型及其运动学 两轮差速底盘（Differential内容请搜索靠谱客的其他文章。