高等数学Mathematica实验题——1.3-5.簧舌线轨迹线直角坐标的求解

81 阅读 0 评论 54 点赞

我是靠谱客的博主自信夏天，最近开发中收集的这篇文章主要介绍高等数学Mathematica实验题——1.3-5.簧舌线轨迹线直角坐标的求解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

首先，这道题目虽然花费我时间比较多，但感觉挺值，挺有成就感。

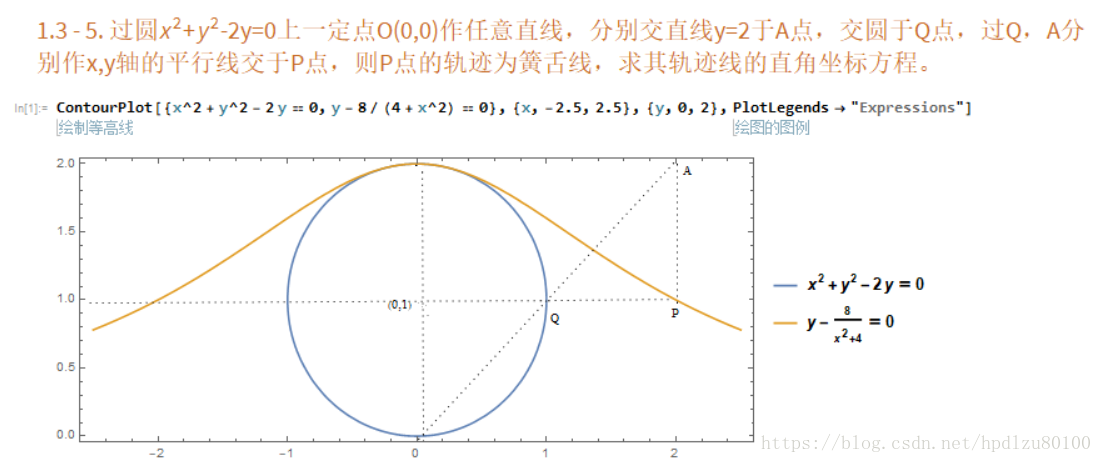
题目：1.3 - 5. 过圆x^2+y^2-2y=0上一定点O(0,0)作任意直线，分别交直线y=2于A点，交圆于Q点，过Q，A分别作x,y轴的平行线交于P点，则P点的轨迹为簧舌线，求其轨迹线的直角坐标方程。

解答：

备注：

1. 演算了两遍，用了6页草稿纸（是不是太菜了，哈哈。主要是第一遍出错了，把参数方程形式搞得很复杂，没法转化成直角坐标方程）

2. 解题过程：为了获取P点的纵坐标，引入参数t（OQ与x轴正半轴的夹角），在圆上，tant=y/x, 将y=xtant代入圆的方程，求出Q点的参数方程坐标：x=2tant/(1+tant^2), y=2tant^2/(1+2tant^2)。

P点的纵坐标和Q点相同，即 y=2tant^2/(1+2tant^2)。P点的横坐标为Q点的横坐标加P、Q两点间的距离，即|AP|*cot(t)=(2-y)/tant=2/(tant*(1+tant^2)). 求得P的横坐标x=2/tant. 由此得P点的参数方程，将其转化为直角坐标方程为：y=8/(4+x^2)

3. 在Mathematica中绘制图形时，遭遇了Mathematica程序奔溃，花了半天的图形不见了。又重新画了一遍。现在学老实了，时不时手动保存一下。