概述
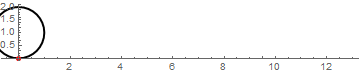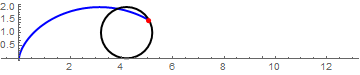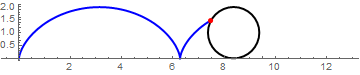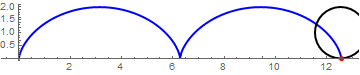
圆球上的某个点的运动轨迹可以分解成两个部分，第一部分为圆球整体的平移运动，第二部分为圆球原地的滚动。不难推出摆线的方程为x=t-sin(t), y=1-cos(t) （假设圆球的平移速度为1m/s,如果速度为v,则两个方程右侧都乘以v即可)。
Mathematica代码为：
Export["RolliingBall.gif",
Table[Show[{ParametricPlot[{t - Sin[t], 1 - Cos[t]}, {t, 0.01, t},
PlotStyle -> {Thick, Blue}],
Graphics[{Thick, Circle[{t, 1}, 1]}],
Graphics[{Red, Disk[{t - Sin[t], 1 - Cos[t]}, 0.1]}]},
PlotRange -> {{0, 2*2*Pi}, {0, 2}}], {t, 0, 2*2*Pi, 1.0/25}]]
最后
以上就是善良蛋挞为你收集整理的Mathematica描绘滚球某个点的运动轨迹（摆线）的全部内容，希望文章能够帮你解决Mathematica描绘滚球某个点的运动轨迹（摆线）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![[HNOI2011]XOR和路径——高斯消元、随机游走模型[HNOI2011]XOR和路径思路代码](/uploads/reation/bcimg13.png)
发表评论 取消回复