《机器学习实战》第三章：决策树（1）基本概念

1. CH2-kNN（1）        
2. CH2-kNN（2）
3. CH2-kNN（3）
4. CH3-决策树（1）    
5. CH3-决策树（2）
6. CH3-决策树（3）
7. CH4-朴素贝叶斯（1）
8. CH4-朴素贝叶斯（2）
9. CH5-Logistic回归（1）
10. CH5-Logistic回归（2）
======== No More ========

决策树（Decision Tree）

（1）是个基本的【分类】算法。

（2）基本思想：决策树是一种树结构，其中的每个内部节点代表对某一特征的一次测试，每条边代表一个测试结果，叶节点代表某个类或类的分布。决策树的决策过程需要从决策树的根节点开始，待测数据与决策树中的特征节点进行比较，并按照比较结果选择选择下一比较分支，直到叶子节点作为最终的决策结果。

（3）举个例子吧：

比如，两个同班同学A和B，玩一个游戏。A头脑中想着班上的一个同学，让B来猜是谁。B可以不断地通过向A提问，来逐渐缩小猜测范围，比如“这个人是男生还是女生”，“这个人身高是160以下，是160-170，是170-180，还是180以上”，“这个人有没拿过国家奖学金”等等，直到剩下一个或很有限个几个候选人。

嗯...这个过程其实类似于决策树的决策过程，也就是拿到一条待分类的数据，给他进行分类：从决策树的根节点开始，按照一定顺序验证这条数据的特征。在每个特征节点上，按照该数据特征值对应的分类，顺着决策树的边，进入下一层节点，直到到达叶节点，得到最终的决策结果（即标签）。例如...有一家贷款机构拿到了一个人的个人信息（可能是信息泄露了），然后想根据下面这棵决策树，判断这个人有没贷款意向，从而决定要不要给他打骚扰电话：

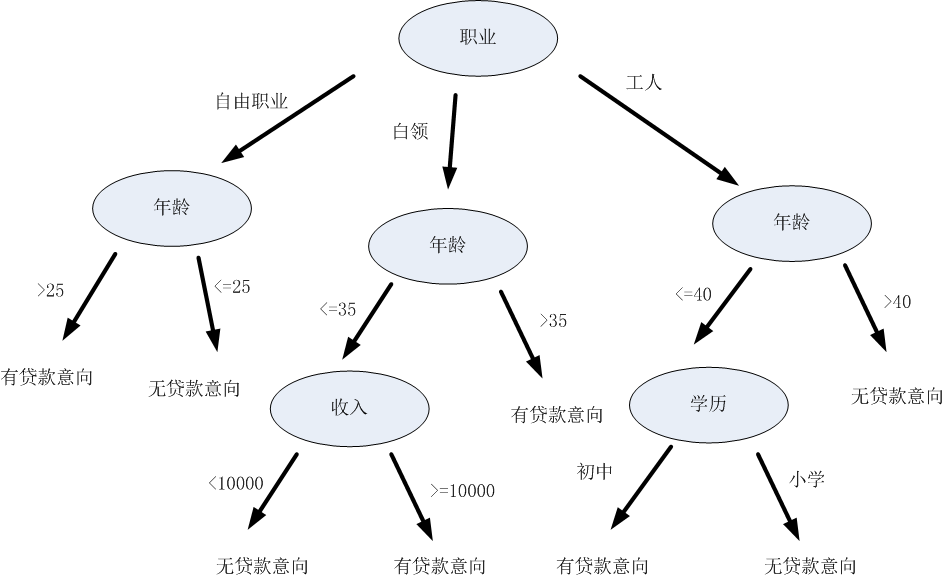
决策树的构造过程，其实就是他的“机器学习过程”，也就是机器根据数据集创建规则的过程。什么规则？就是在树的每一个节点上，究竟该选择哪一个数据属性，来把这个节点中的数据集分开呢？比如上面那个猜同学的游戏，是先问“性别”，还是先问“身高”，才能达到缩小猜测范围的最佳效果呢？

等下会介绍。

（4）优点：复杂度不高

 缺点：可能会产生过度匹配的问题

 适用数据类型：离散型，连续型。

------------------------------------------------------------------------------------------------

信息增益（Information Gain）、熵（Entropy）

回到刚才那个问题，在决策树的每个节点上，究竟是选择哪个特征来把这个节点里的数据集划分开呢？

划分数据集的大原则是：将无序的数据变得更加有序。

那么，怎样度量数据有序还是无序？一种方法就是使用信息论来度量。

在划分数据集之前之后，信息发生的变化称为信息增益。我们希望计算出每个特征值划分数据集获得的信息增益。那么，信息增益最高的特征就是最好的选择。坠吼滴！

对于一个数据集合而言，信息的度量方式称为香农熵，或简称为熵。熵越大，说明数据集越混乱、越无序。一个数据集合，再划分前、划分后，熵的变化，就是信息增益了。信息增益越大，说明数据集合划分之后，有序程度的增加量越大。

那么怎样计算熵呢？熵定义为信息的期望值。如果待分类的事务可能划分在多个分类之中，假设 Xi是其中的一个类，则符号 Xi 的信息定义为：

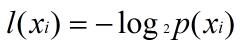
其中，p(Xi) 是选择该分类的概率。

为了计算熵，我们需要计算所有类别的所有可能值所包含的信息期望值：

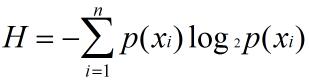
其中，n是分类的数目。

还是来举个栗子：

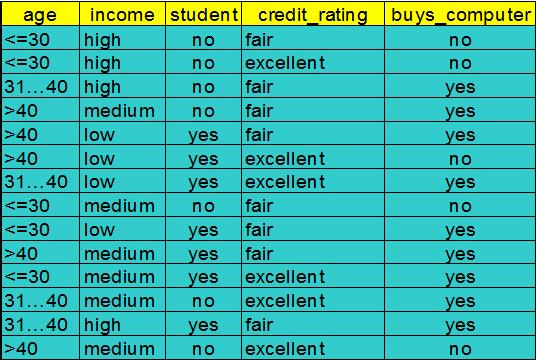
这个例子取自于《数据挖掘：概念与技术》。前4列：age（年龄）、income（收入）、student（是否是学生）、credit_rating（信用评级）是特征值。最后一列：buys_computer（是否买电脑）是分类（也就是标签）。

这里有14条数据，他们现在处于同一个节点之中，我们先用4个特征中的某一个，来划分它们。先算当前没划分时的熵：

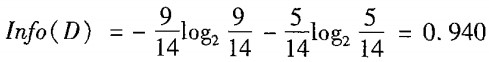
根据最后一列的标签，这对数据有两个分类：yes / no。这14条数据里，有9条的分类是yes，5条是no。那么按上面的公式计算，当前数据集合的熵就是0.940。

接下来，我们看看按照4种特征划分这个数据集合后，熵变成了多少。

首先是age（年龄）。如果按照age来分，那么会分出3个子数据集，因为age有3种不同的特征值：<=30，31-40，>40。

 <=30：一共5条数据，其中2条yes，3条no

30-40：一共4条数据，其中4条yes，0条no

>40：一共5条数据，其中3条yes，2条no

那么，按照age来分的话，划分后的熵就是：

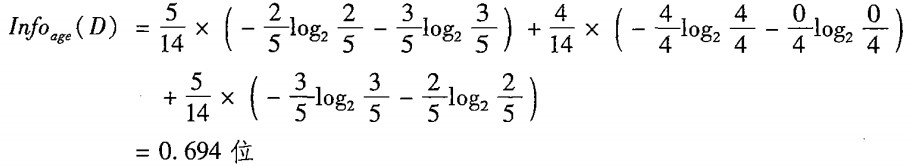
注意，这里计算的是划分后3个子数据集的熵的总和，每个子数据集的熵之前还乘上了一个权重，也就是这个子数据集的概率。

然后，拿划分前的熵减划分后的熵，就得到了信息增益：

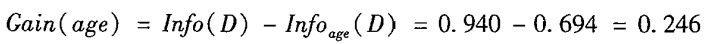
接下来算按照income、student、credit_rating来划分的情况，过程一样的：

Infoincome(D) = 4/14 * [ -2/4*log(2/4) - 2/4*log(2/4)] + 6/14* [ -4/6*log(4/6) - 2/6*log(2/6)] + 4/14* [ -3/4*log(3/4) - 1/4*log(1/4)]

Gain(income) =0.029

Infostudent(D) = 7/14 * [ -3/7*log(3/7) - 4/7*log(4/7)] + 7/14* [ -1/7*log(1/7) - 6/7*log(6/7)]

Gain(student) =0.151

Infocredit_rating(D) =  6/14 * [ -3/6*log(3/6) - 3/6*log(3/6)] + 8/14 * [ -6/8*log(6/8)- 2/8*log(2/8)]

Gain(credit_rating) = 0.048

比较之后，发现按照 age 划分，信息增量是最大的。所以在这个节点，我们决定按照 age 来进行划分。

哦对了，以上的算法是ID3算法。它倾向于选择具有大量值的属性，即值比较分散的属性。除此之外还有C4.5算法。它引入了增益率（gain ratio）的概念，具体就不介绍了。

嗯，决策树最核心的部分应该就是这些了。下一篇博客上代码。

最后

以上就是香蕉鸡翅为你收集整理的《机器学习实战》第三章：决策树（1）基本概念的全部内容，希望文章能够帮你解决《机器学习实战》第三章：决策树（1）基本概念所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。