决策树(decision tree)是一种常见的机器学习算法,是通过树形结构进行决策的,如下图:
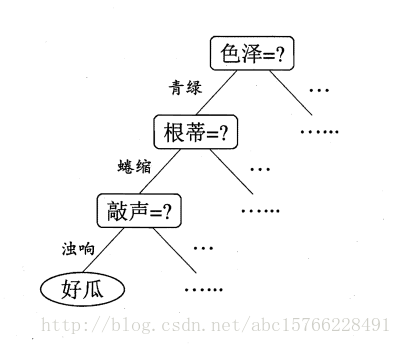
通过分支节点的判断进行分类,具体算法如下:

这里1行是说,初始化出一个节点node是根节点,然后,2-4是说,如果类别相同,既y1=y2=。。。。=ym,则node为叶子节点,分类结束,5-7行是说,如果a1=a2=…..=am,则,属性无法区分出类别,那么,node为叶子节点,类别为max(Y1,y2,……,Yn)。第8行,选择出最优的划分属性a*,具体方法后面说。第9-16行是说,为这个属性中的每个值都做出一个分支,并且为每个分支迭代这个算法。11-12行,是说,如果某个属性的对应的样本子集为空,则用先验分布,取整个样本集中最多那个类作为叶子节点的分类。14行是说,去掉a*的属性,递归这个算法。最终会生成一棵决策树。
划分选择
信息熵:“信息熵”(information entropy)是衡量样本集合纯度的最常用的指标之一。假定样本集合D中第K类样本占比pk(k=1,2,…,|y|),则,D的信息熵为:
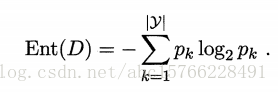
熵越小,纯度越高。
信息增益:用划分前的熵值减去划分之后,每个分支的熵和其权重的乘积,权重为这个分支中的样本数目和样本总数的比值。
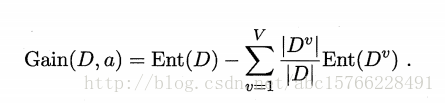
一般来讲,信息增益越大,意味着用这个属性所获得的“纯度”的提升越大。因此,我们可以用信息增益来进行决策树的划分,信息增益越大越好,表示这个属性可以让决策树的“纯度”提升越大。
增益率:这里有个问题,假设,将“序号”也作为一个属性,那么,“序号”这一列的信息增益必然最大,但是,这个属性毫无意义,这里用增益率进行修正。著名的C4.5算法中,用增益率而不是信息增益,作为划分准则。其定义为:
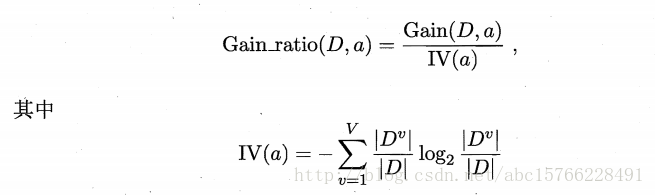
称为属性a的固有值。固有值a可能的取值越多,固有值越大。
因此,C4.5算法并不是直接选择信息率最大的候选划分属性,而是用了一个启发式:先从候选划分属性中找出信息增益高于平均水平的属性,再选择增益率最高的。
基尼指数:CART使用基尼指数选择属性划分。其中,基尼值表达式为:
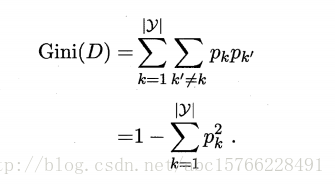
基尼指数越小,纯度越高,直观来看,其表达了随机抽取两个样本,标记不同的概率。基尼指数的表达式为:
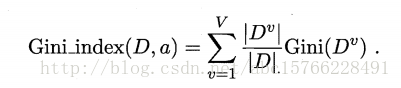
剪枝处理:剪枝是决策树对付“过拟合”的方法,有时候也会欠拟合。
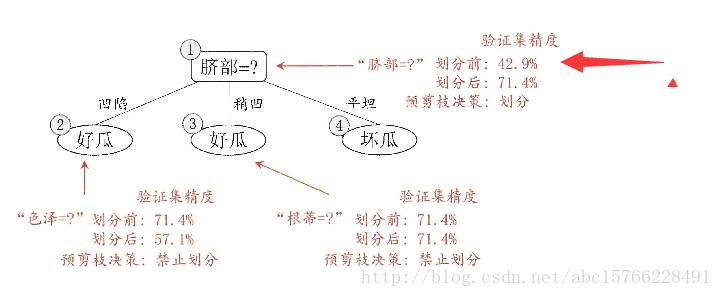
预剪枝:在构建决策树的过程中,通过验证集精度确定要不要剪枝,换句话说,把验证集带进去,看下结果,变好了,就分,变不好,就部分。如下图:
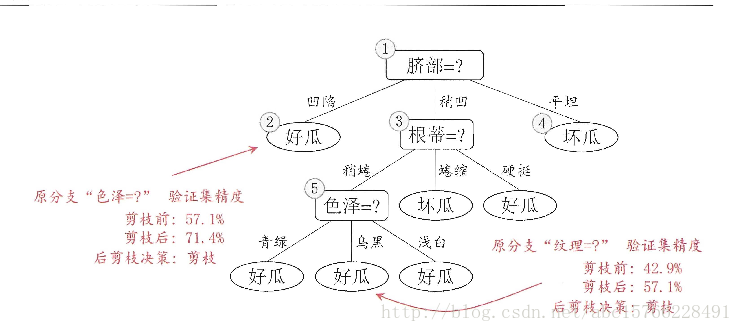
后剪枝:同理,但是是在一颗决策树建立好之后进行的。如果剪枝之后验证集的精度提高,那么剪枝,否则不剪枝
如下图:
连续与缺失值
连续值处理:当某个属性是连续值时,我们可以对其每个属性值进行划分,选择信息增益最大的那个属性,作为划分值(C4.5采用这种二分法处理),如下:
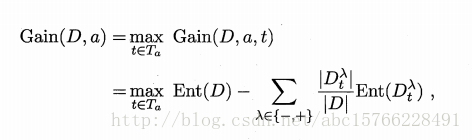
缺失值处理:
我们要解决:(1)有缺失值时如何划分属性,(2)如何将有缺失值的样本划分到某个属性中。
首先,定义三个值:
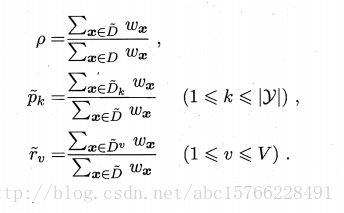
其中,第一个值是无缺失样本占的比例;第二个值是无缺失值中第k类占总的样本的比例,第三个值是无缺失值样本在属性a上取a的第v个属性(a^v)占总样本的比例,于是,可以将信息增益和信息熵推广到下面这个式子(下面的式子是信息熵):
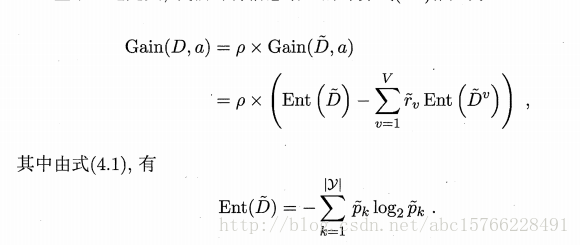
我们可以用无缺失值建立一颗决策树,然后,将具有未知属性的样本划分入所有的子节点,其样本权值在与属性值a^v对应的子节点中调整为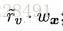 ;
;
就是说,这个样本的权重,是乘了一定概率的,就是说,是以一定概率分到各个属性下面的。
多变量决策树:若我们把每个属性视为一个坐标轴,那么,决策树的边界是多个与坐标轴平行的线段组成。如图:
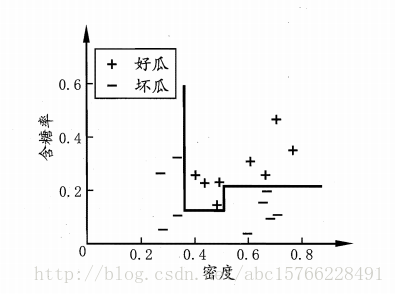
优点,有较好的解释性,缺点:比较复杂,要化好多段才能划分开。
改进:多变量决策树:是对一些属性的线性组合,就是形如一个线性分类器,如图:
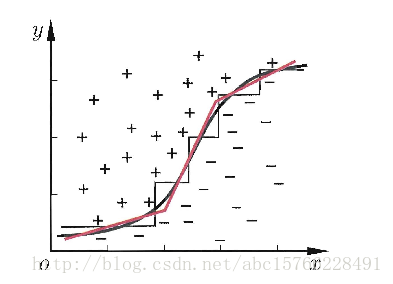
例如建立下面的决策树:
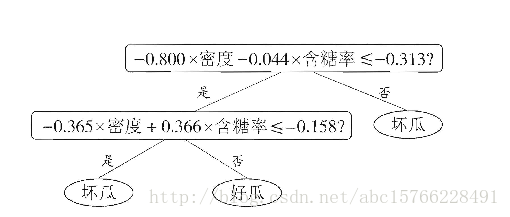
对应的分类边界是:
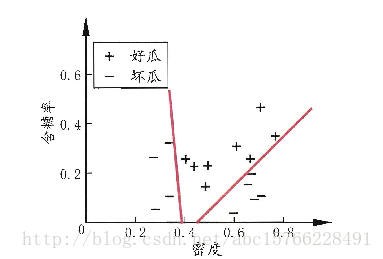
以上图片均来自周志华老师的《机器学习》一书
至此,决策树的有关内容基本告一段落。。。。
最后
以上就是优秀猎豹最近收集整理的关于决策树学习笔记的全部内容,更多相关决策树学习笔记内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复