斯坦福CS231n 课程学习笔记--线性分类器（笔记篇）

最近学习了斯坦福的CS231n(winter 2016)系列课程，收获很大，作为深度学习以及卷积神经网络学习的入门很是完美。学习过程中，主要参考了知乎上几位同学的课程翻译，做得很好，在这里也对他们表示感谢，跟课程相关的很多资源都可以在该专栏中找到。推荐大家把每个笔记的翻译都完整的看一下。关于该课程视频的中文字幕也在翻译进行中，目前第一集已经翻译完成，感兴趣的同学可以也可以看看参与进去。此外，完成课程视频和笔记的阅读之后也对课程的3个Assignment进行了实现。接下来主要以对课程笔记总结和Assignment代码实现相结合的方式完成这一系列的博客。

本篇博客主要参考了课程的官方笔记和知乎上关于线性分类器笔记的三篇翻译。如下图：

主要从评分函数，损失函数，参数优化三个部分进行介绍，这也是大多数分类器的三大组件，分别对应于模型、目标、学习。
首先说一下数据集（包括训练集、验证集（用于超参数调优）和测试集），训练集X是一个大小为[N*D]的矩阵，表示共有N个样本，每个样本都由D维特征构成；y是其标签，大小为[1*N]，分别对应N个样本，且yi属于1,2,3…,C，共有C个类别。

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

1，评分函数就是一个将原始图像数据转换到分类标签的参数化映射（Parameterized mapping from images to label scores）。对于线性分类器而言，就是下面的线性映射：
………………………………………………………………. f(xi, W, b) = Wxi + b ……………………………………………………………………..
xi为一张图片拉伸成一个长度为D的列向量，W是大小为[C，D]的权重矩阵，b是[C,1]的偏置向量，f最后为[C,1]的评分向量，表示样本在每一个类别上的得分。其中W的每一行都表示为一个类别的分类器，共C个类别，与xi相乘之后得到一个分数（可以理解为相似度），其实就是从训练集中为每一个类别抽象出一个模板保存在W中，然后将新的图像与这C个模板相比较，最相似的就当做是其类别。所以训练分类器的目的就是从训练集中学习到最优的参数W和b（其实可以通过给x和W分别扩展一个维度将b融到其中，见下图）。

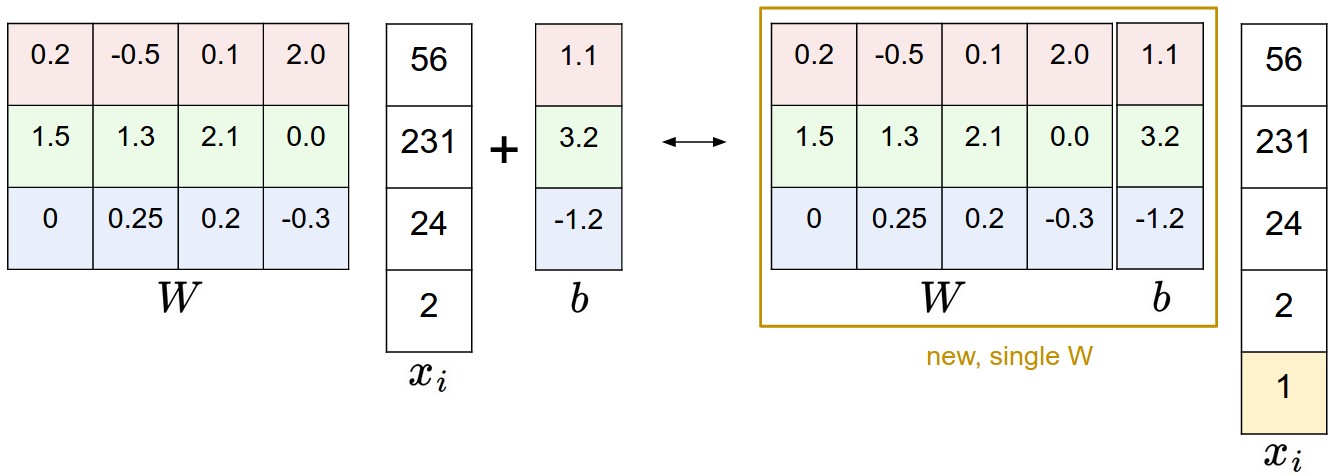
举一个直观的例子来说明上述f分值的计算过程，如下图所示：

这里从最终的评分来看，狗的分值最高，那是因为W和b的参数设置太差，还需要继续训练直到猫的得分远高于另外两类。

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

2，从上面的例子中可以看出W并不是我们想要的结果，那么如何评价抽象出的W的好坏呢，就是下面要介绍的损失函数了。损失函数一般包括数据损失和正则损失两部分。常见的损失函数包括多类支持向量机损失函数（Multiclass Support Vector Machine loss）和交叉熵损失函数（cross-entropy loss），分别应用于SVM分类器和softmax分类器。接下来分别进行介绍：

1，这里先介绍一下正则损失，笔记中引入正则化是因为W不唯一性，但其实正则化还有很多好处，比如可以防止过拟合等等。常用的正则化惩罚包括L1、L2等，可以理解为对参数添加惩罚项，来抑制模型过于复杂，和参数过大等现象。这里使用L2范式作为正则损失计算方法，其实就是W中每个参数的平方求和（L2倾向于使W中的参数更小且分布更加分散，即希望最终的模型是由所有特征一起做贡献，而不是依赖于某些重要的特征）。公式如下：
………………………………………………………………..……………………………………………………………………..

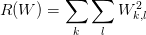2，然后介绍一下SVM loss。对于某个样本（xi，yi）而言，使用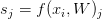来表示其得分向量中的第j类的得分（这里可能有些拗口，就拿上面猫的例子来讲，最终得分f(xi,W)就是一个三维向量，j就取值0，1，2，sj分别代表-96.8,437.9,61.95，而syj就表示其真是类别的预测得分，在这里就是猫类别的得分-96.8），其多类支持向量机损失函数计算公式如下：
………………………………………………………………..……………………………………………………………………
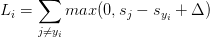其中Delta为边界值，是一个超参数，一般取1即可（因为其和正则化损失的参数lambda起到相同的作用，所以固定一个，调整另外一个即可）。max函数也称为折页损失（Hinge loss），有时也用折页平方损失max(0, -)^2。上述损失函数的意义如下图所示：

多类SVM“想要”正确类别的分类分数比其他不正确分类类别的分数要高，而且至少高出delta的边界值。图中蓝色为正确分类得分，绿色为其他类别得分，红色长度为delta。如果绿色线进入了红色的区域，甚至超过了蓝色线，那么就说明该类错误，开始计算损失。如果没有这些情况，则分类正确，损失值为0（max）。

所以结合SVM loss和正则损失就可以得到完整的损失函数，lambda为超参数，可以使用交叉验证调整如下所示：

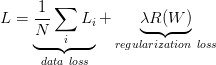
或者展开形式：

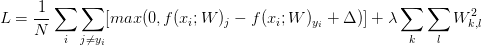
3，softmax分类器损失函数：其实softmax分类器就是将两类逻辑回归扩展到多类情况。相比SVM分类器而言，SVM把f当做分类评分，而softmax计算其归一化分类概率，更加直观（所有类别得分求和为1，得分即为其类别概率）。softmax使用交叉熵损失替代折页损失，计算公式如下：
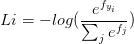…………………………………………… 或者展开 ……………………………………………………….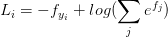
对该公式的理解：

不过由于e的指数值会很大，在实际计算过程中会遇到数值稳定性问题。所以使用下面的公式代替：
……………………………………………………………………………………………………………………..
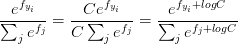其中logC一般取fj的最大值的负数，从而使fj+logC最大为0，进而解决数值稳定的问题。所以结合正则化损失，softmax完整的损失函数如下所示（1为示性函数）：

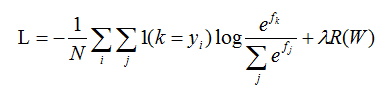
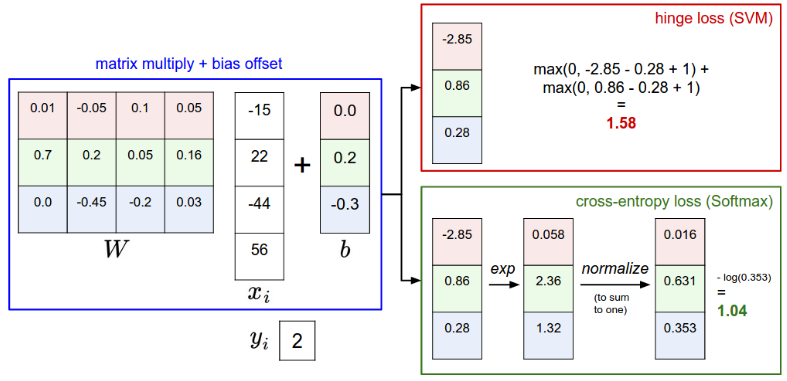
这里用一张图来表示SVM和softmax之间的区别：

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

3，讲完了评分函数和损失函数，接下来就要介绍一下参数优化过程了。有了损失函数，我们就知道了一个W的好坏，那么如果现在的W不好，我们应该以什么样的方式进行修改和更新W呢？那就是梯度下降（Gradient Descent）和反向传播（backpropagation）相结合的方法。

1，梯度计算。梯度下降法就是找到是loss函数降低最快的W更新方式（类比于下山，我们总是希望沿着最陡峭的方向下山速度最快）。梯度的计算方法主要包括数值梯度计算（慢，简单）和分析梯度计算（迅速准确，但是复杂，需使用微分公式推导）。

对于数值计算法，即使用有限差值计算梯度。使用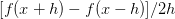 这个公式计算f在x处的梯度。h取10^-5，即一个很小的常数。相比 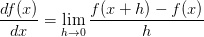这个公式，虽然前面一个需要计算两次f函数的值，但是前者精度更高（根据泰勒展开式，前者的误差是平方项，而后者是一次项。所以一般使用前者）。
计算出剃度之后，就按照W_new = W - step_size * df 对W进行更新（这里使用减号，即在梯度负方向上进行更新（Update in negative gradient direction））。不过在计算过程中要注意步长step_size（也叫作学习率）的选取，梯度只告诉了我们接下来要走的方向，却没有说明要走多远，如下图所示，步长选择的合适我们可以很快到达最优解。但是如果步长过大，会使错过最优解。所以一定要选取合适的步长（超参数）。

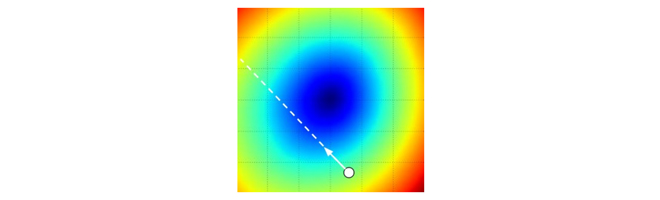
对于分析梯度方法，其实就是使用公式推导的方式得到梯度的计算公式。相比数值梯度计算（不精确，消耗计算资源）而言，微分分析法速度很快。但是公式推导过程很容易出错，所以一般使用梯度检查 （gradient check）的方法，将二者进行比较。对SVM的损失函数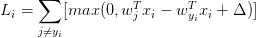 而言，其导数为：

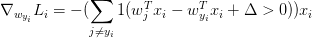
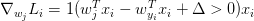
此外，在实际使用过程中，由于训练集往往都是百万量级，如果为了得到一个参数更新而遍历整个训练集，太浪费资源了，所以经常使用小批量数据梯度下降法MGD （Mini-batch gradient descent）（一般取100，200等），若取极端将批量=1，即每次只对一个样本进行计算，称为随机梯度下降SGD（Stochastic Gradient Descent），但很少用。往往不区分SGD和MGD的区别。

2，反向传播。反向传播就是利用链式法则（chain rule 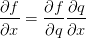）递归计算表达式的梯度的方法。这一部分要好好看看笔记和视频，因为理解反向传播对于理解神经网络而言至关重要。随堂笔记中举了几个例子建议好好看一下。
根据链式法则，将复杂的计算公式简化为小的计算单元组成的计算链路。在计算链路中，每个单元只需要计算其输出和关于输入的局部梯度，而不需要在意其他环节（独立）。然后反向传播过程中，每个单元将回传的梯度乘以其局部梯度就得到了整个网络输出对于其输入的梯度。结合下面的例子加以理解：

# 设置输入值
x = -2; y = 5; z = -4
# 进行前向传播
q = x + y # q becomes 3
f = q * z # f becomes -12
# 进行反向传播:
# 首先回传到 f = q * z
dfdz = q # df/dz = q, 所以关于z的梯度是3
dfdq = z # df/dq = z, 所以关于q的梯度是-4
# 现在回传到q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. 这里的乘法是因为链式法则
dfdy = 1.0 * dfdq # dq/dy = 1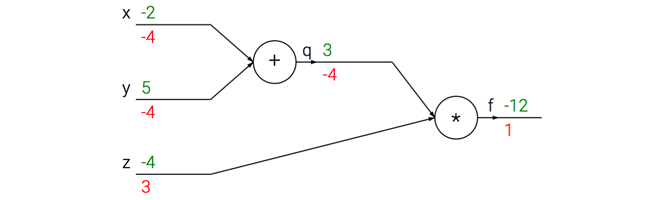

在实践过程中常常使用分段反向传播，即将前向传播的代码分成不同阶段，并使用中间变量保存每个阶段的计算结果，这样在反向传播过程中就可以方便地使用链式法则计算出梯度。见笔记中sigmoid和分段计算的例子。此外向量操作的梯度计算方法只需要考虑清楚维度关系即可得到正确的答案。例如：

# 前向传播
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)

# 假设我们得到了D的梯度
dD = np.random.randn(*D.shape) # 和D一样的尺寸
dW = dD.dot(X.T) #.T就是对矩阵进行转置
dX = W.T.dot(dD)

到这里已经完成了这部分的笔记总结，下一篇文章中将会把Assignment1中除了神经网络部分的内容完成。其实其课程官网上已经给出了很详细的实现步骤，要补充的代码不是特别多，主要是对笔记中的梯度计算、反向传播、交叉验证等部分进行训练和加强。

最后

以上就是笑点低月亮为你收集整理的斯坦福CS231n 课程学习笔记--线性分类器（笔记篇）的全部内容，希望文章能够帮你解决斯坦福CS231n 课程学习笔记--线性分类器（笔记篇）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。