PCA+核函数（高斯）提取特征代码+图视

大数据时代，什么维度灾难问题的出现，所以需要提出 降维处理保留数据结构，减少算法运行时间，pca，kpca,svm等是一种

有效的特征提取方法，这里就不balabala说为什么要有这些技术以及他们的使用方法，下面直接代码展示。

自己代码生成一组数据，对其用pca和kpac进行特征提取并比较效果，由下图可以得知kpac效果更明显

本文用的是高斯核函数：

高斯核定义输入空间的两个点

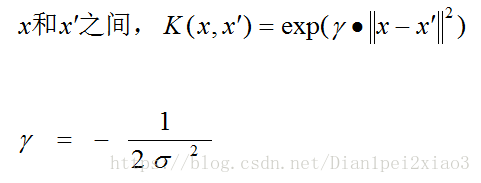
更多关于上面的信息：http://en.wikipedia.org/wiki/Radial_basis_function_kernel

scikit-learn里的核pca对象也可以使用其他类别的核：

线性

多项式

Sigmoid

from sklearn.datasets import make_circles

import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.decomposition import KernelPCA
#生成一个变化非线性的数据集
np.random.seed(0)
x,y=make_circles(n_samples=400,factor=.2,noise=0.02)
#为生成的数据集绘制图形 
plt.close('all')
plt.figure(1)
plt.title("Original Space")
plt.scatter(x[:,0],x[:,1],c=y)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
#试试用普通的PCA处理这个数据集 
pca=PCA(n_components=2)
pca.fit(x)
x_pca=pca.transform(x)
plt.figure(2)
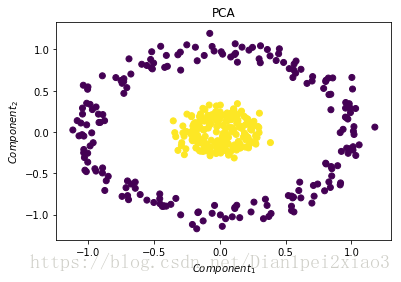
plt.title("PCA")
plt.scatter(x_pca[:,0],x_pca[:,1],c=y)
plt.xlabel("$Component_1$")
plt.ylabel("$Component_2$")
#应用普通的PCA，绘出第一个主成分
class_1_indx=np.where(y==0)[0]
class_2_indx=np.where(y==1)[0]
plt.figure(3)
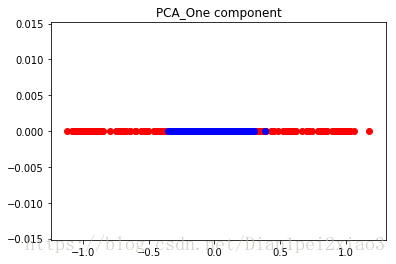
plt.title("PCA_One component")
plt.scatter(x_pca[class_1_indx,0],np.zeros(len(class_1_indx)),color='red')
plt.scatter(x_pca[class_2_indx,0],np.zeros(len(class_2_indx)),color='blue')
#rbf(radial basis function)径向基函数
kpca=KernelPCA(kernel="rbf",gamma=10)
#执行核pca
kpca.fit(x)
x_kpca=kpca.transform(x)
#绘制前两个主成分
plt.figure(4)
plt.title("Kernel PCA")
plt.scatter(x_kpca[:,0],x_kpca[:,1],c=y)
plt.xlabel("$Component_1$")
plt.ylabel("$Component_2$")

plt.show()

v

最后

以上就是爱笑书包为你收集整理的PCA+核函数（高斯）提取特征代码+图视的全部内容，希望文章能够帮你解决PCA+核函数（高斯）提取特征代码+图视所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。