一，有序齐次单项式空间
2阶有序齐次单项式：
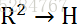
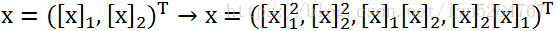
由此推广，可以得到d阶的有序齐次单项式：
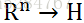
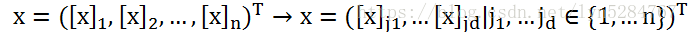
由上式可知，如果n和d数据过大时，内积的运算量将会非常大。
我们观察二阶有序齐次单项式，在H中做内积有：
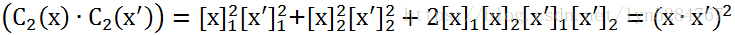
我们定义函数：
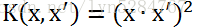
由此我们推算到d阶的有序齐次单项式：
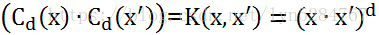
二，有序单项式空间
类似的可以推导出，二阶有序单向式空间：
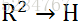
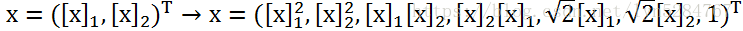
类似的推导到多阶：
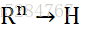
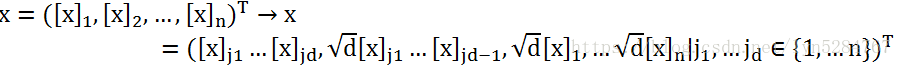
类似推定义函数：
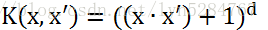
推算到d阶的有序单项式：
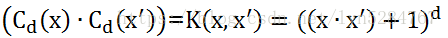
三，无序单项式空间
在上述有序的单项式中，我们把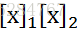
和
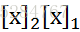看做不同的分量而区分，而实际上我们可以把它看做是无序的，相等的，将映射调整为：
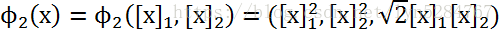
仍然可以得出：
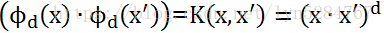
四，Hilbert空间与多项式核函数
由前面可知支持向量分类机只与内积有关系，而与映射到的Hilbert空间并无直接联系，所以以后我们只关系内积。我们把此函数统称为多项式核：
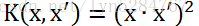和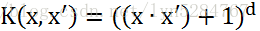
例子
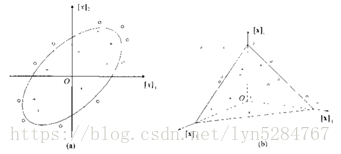
假设一个椭圆可以对类进行划分（如图（a））：
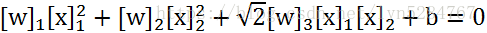
引入非线性映射：
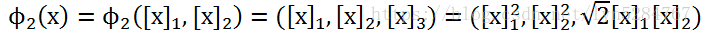
获得三维空间，使用支持向量机分划超平面（如图(b)）:
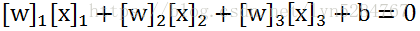
最后
以上就是威武水池最近收集整理的关于第三章-3.2多项式空间和多项式核的全部内容，更多相关第三章-3内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复