Objective-C 判断两个矩形是否相交

86 阅读 0 评论 57 点赞

我是靠谱客的博主轻松麦片，最近开发中收集的这篇文章主要介绍Objective-C 判断两个矩形是否相交，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

问题定义：定义一个矩形类，实现判断矩形是否相交的方法。

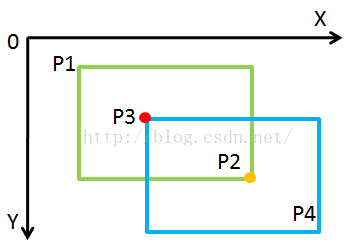
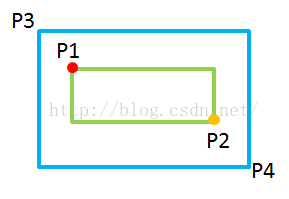
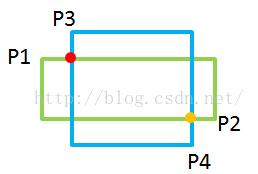
思路：给定两个边与坐标轴平行的矩形，分别由左上角与右下角两点指定，即矩形(P1，P2)与(P3，P4)，判断两矩形是否相交。如下图所示，首先求出P1与P3点在X方向较大值与Y方向较大值的交点，在下图中就是P3，用红点(记为M点)表示。然后求出P2与P4点在X方向较小值与Y方向较小值的交点，在下图中就是P2，用橙色点(记为N点)表示。如果M点的X坐标和Y坐标值均比N点相应的X坐标和Y坐标值小，亦即M和N可以分别构成一个矩形的左上角点和右上角点，则两矩形相交；其余情况则不相交。

WFRect

#import <Foundation/Foundation.h>

@interface WFRect : WFShape

@property (nonatomic,assign) double width;

@property (nonatomic,assign) double height;

+ (instancetype) rectWithX : (double) x

y : (double) y

width: (double) width

height: (double) height;

- (instancetype)initWithX : (double) x

y : (double) y

width: (double) width

height: (double) height;

@end

WFRect.m

#import "WFRect.h"

@implementation WFRect

+(instancetype)rectWithX:(double)x

   y:(double)y

width:(double)width

height:(double)height{

  return [[self alloc] initWithX:x y:y width:width height:height];

}

- (instancetype)initWithX:(double)x

y:(double)y

   width:(double)width

height:(double)height{

  if (self = [super init]) {

_x = x;

_y = y;

  _width = width;

  _height = height;

}

  return self;

}

-(BOOL) intersects:(WFRect *) other{

  double redX = _x > other.x ? _x : other.x;

  double redY = _y > other.y ? _y : other.y;

  double yellowX = _x + _width < other.x + other.width ?_x + _width : other.x + other.width;

  double yellowY = _y + _height < other.y + other.height ? _y +_height : other.y + other.height;

  return (yellowX > redX && yellowY > redY);

}

@end