分享一个小方法，判断同一坐标系下两个矩形是否有重合

1
2
3
4
5
6
7
8
9
10
11
12
最近项目中遇到一个问题，需要判断两个矩形是否有重合，以及重合的面积是否超过指定值。
其实是一个很简单的数学问题，这里发出来给大家分享一下。

先说思路，**同一坐标系下**，判断两个矩形是否有重合，有以下三种情况：
1、两个矩形，其中一个包含在另一个之中，这种肯定是重合的；
2、两个矩形，完全不重合，即没有交叉重合的区域；
3、两个矩形，有部分重合在一起，形成一个新的重合矩形。

我们这里说一下第三种情况
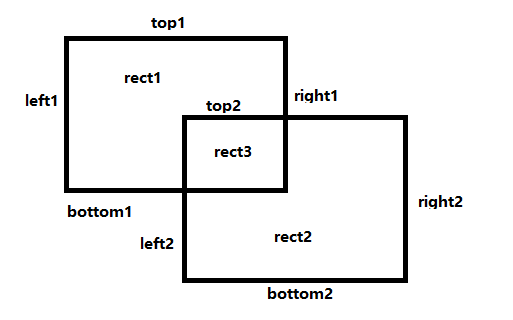
矩形rect1和rect2交叉，形成新的重合矩形rect3，根据图形可以看出，
矩形rect3的Left=rect2.Left,Top=rect2.Top,Right=rect1.Right,Bottom=rect1.Bottom。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
			  /// <summary>
        /// 判断两个矩形是否重合（重合部分大于较小矩形面积的一定比例）
        /// </summary>
        /// <param name="rect1">矩形1</param>
        /// <param name="rect2">矩形2</param>
        /// <param name="ratio">重合矩形面积与较小矩形面积的比率（百分比）</param>
        /// <returns></returns>
        public static bool RectIsCoincide(Rectangle rect1, Rectangle rect2, int ratio)
        {
            if (rect1.Width <= 0 || rect1.Height <= 0 || rect2.Width <= 0 || rect2.Height <= 0)
                return false;

            //两个矩形其中一个包含在另一个之中
            if (rect1.Contains(rect2) || rect2.Contains(rect1))
                return true;

            int maxLeft = rect1.Left > rect2.Left ? rect1.Left : rect2.Left;//两个矩形较大的left值
            int maxTop = rect1.Top > rect2.Top ? rect1.Top : rect2.Top;//两个矩形较大的top值
            int minRight = rect1.Right < rect2.Right ? rect1.Right : rect2.Right;//两个矩形较小的right值
            int minBottom = rect1.Bottom < rect2.Bottom ? rect1.Bottom : rect2.Bottom;//两个矩形较小的bottom值

            //如果两个矩形有重合，初始化一个新的重合部分矩形
            int newRectLeft = 0, newRectTop = 0, newRectWidth = 0, newRectHeight = 0;
            //如果有重合部分
            newRectLeft = maxLeft;//重合矩形的左上角X坐标即Left=偏右侧矩形的X坐标即Left
            newRectTop = maxTop;//重合矩形的左上角Y坐标即Top=偏下侧矩形的Y坐标即Top
            newRectWidth = minRight - maxLeft;//重合矩形的宽度=偏左侧矩形的Right-偏右侧矩形的Left
            newRectHeight = minBottom - maxTop;//重合矩形的高度=偏上侧矩形的Bottom-偏右侧矩形的Top

            //如果新矩形的宽高均大于0，则证明重合部分存在
            if (newRectWidth > 0 && newRectHeight > 0)
            {
            	//这里是为了判断重合矩形的面积与面积较小一个矩形面积的比率，如果超过设定的比例就返回true
                int minArea = rect1.Width * rect1.Height < rect2.Width * rect2.Height ? rect1.Width * rect1.Height : rect2.Width * rect2.Height;
                if (newRectWidth * newRectHeight > ((float)minArea * ratio / 100))
                    return true;
            }

            return false;
        }