仿射变换的原理

在条形码识别软件中有图像预览的功能。有时预览的图像需要进行转置（旋转180度或者90度）、缩放、镜像（左右反转）等操作。OpenCV提供了相应的函数进行以上操作。例如： 
转置：cv::WarpAffine() 
缩放：cv::resize() 
镜像：cv::remap() 
如果同时要转置，缩放和镜像，就需要进行三次图像运算。其实以上三个操作都是同一类型的变化，称作仿射变化。可以把这3次图像运算合并成一次，从而优化运算时间。如何合并这三次运算，需要从仿射变换的原理说起。

举个例子，我们需要对以下图像（蓝色）顺时针旋转90度（橙色），可以这么做：假设原来的图像宽w高h 

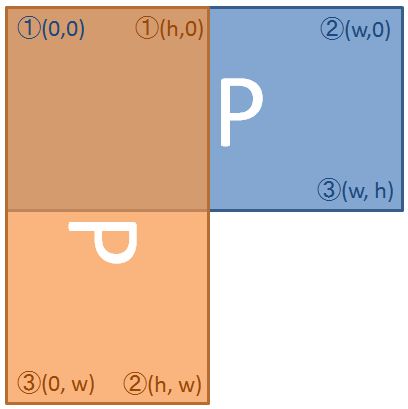
(1) 创建宽h高w内存区域存放新图像； 
(2) 逐一把原图像中的像素(x0,y0)搬到新图像的对应像素(x1,y1) 
例如原图像的左上角点①(0,0)被搬到新图像的右上角(h,0)； 
右上角点②(w,0)被搬到新图像的右下角(h,w)； 
右下角③(w, h)被搬到新图像的左下角(0,w) 
以此类推，可以发现(x0, y0)和(x1, y1)之间存在以下规律： 
X1=-y0+h; y1=x0;
对于其他各种几何变换，平移、缩放、镜像等，我们都可以用类似的方法进行运算。因此可以把上式写成通用的形式：

x1=ax*x0+bx*y0+cx

y1=ay*x0+by*y0+cy

在顺时针旋转90度的例子中，

 ax=0,bx=1,cx=0;ay=−1,by=0,cy=w 

更一般的，我们可以把上面写成矩阵形式：

我们把矩阵 MT=⎛⎝⎜axay0bxby0cxcy1⎞⎠⎟ 称作仿射矩阵。

最后

以上就是喜悦柜子为你收集整理的仿射变换的原理的全部内容，希望文章能够帮你解决仿射变换的原理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。