1. 首页
  2. 文章中心
  3. 数据结构

二叉搜索树基本原理与C语言实现

113 阅读 0 评论
我是靠谱客的博主 清爽大神，这篇文章主要介绍二叉搜索树基本原理与C语言实现，现在分享给大家，希望可以做个参考。

1：二叉搜索树的客观认识
      二叉搜索树又称二叉排序树，即对一棵树按照中序遍历之后，每个节点的属性值是按照顺序排列的，如下图：

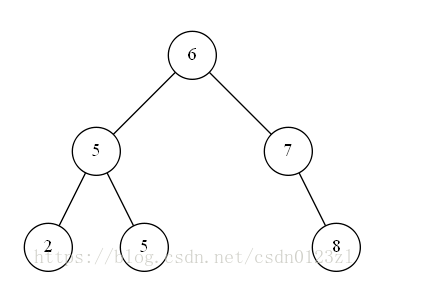
对上图的树按照中序遍历得到的属性值依次为(2,5,5,6,7,8)，可以发现得到的属性值是按照从小到大排序的。

2：二叉搜索树的性质

     对于二叉搜索树的每一个节点，如果它的左孩子不为NULL，那么它左孩子的属性值 <= 它的属性值；如果右孩子不为NULL，那么它的右孩子的属性值 >= 它的属性值。

3：二叉搜索树的作用

     假设我们现在有一个数据集，且这个数据集是顺序存储的有序线性表，那么查找可以运用折半、插值、斐波那契二等查找算法来实现，但是因为有序，在插入和删除操作上，就需要耗费大量的时间（需进行元素的移位），能否有一种既可以使得插入和删除效率不错，又可高效查找的数据结构和算法呢？

       首先解决一个问题，如何使插入时不移动元素，我们可以想到链表，但是要保证其有序的话，首先得遍历链表寻找合适的位置，那么又如何高效的查找合适的位置呢，能否可以像二分一样，通过一次比较排除一部分元素。那么我们可以用二叉树的形式，以数据集第一个元素为根节点，之后将比根节点小的元素放在左子树中，将比根节点大的元素放在左子树中，在左右子树中同样采取此规则，如下图（此处参考https://www.cnblogs.com/tz346125264/p/7766643.html）

        那么在查找x时，若x比根节点小可以排除右子树所有元素，去左子树中查找（类似二分查找），这样查找的效率非常好，而且插入的时间复杂度为O（h），h为树的高度，较O（n）来说效率提高不少。

下面给出二叉搜索树的C语言版本的实现，可以进行简单的创建二叉搜索树，插入数据，删除数据，中序遍历搜索树，销毁树。工具使用的是VS2010，感兴趣的小伙伴可以使用C++模板技术进行更加精细的封装，笔者水平有限，有误请指出，感激不尽。

1. 二叉搜索树的头文件  BST.h

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#pragma
#include<stdio.h>

//定义树的数据结构
struct BstNode
{
	int val;
	BstNode *left;
	BstNode *right;
	BstNode(int x) : val(x),left(NULL),right(NULL) {}
};

typedef void BstRoot; //数据结构类型重定义

//插入数据
int InsertNode(BstRoot *Root,int data);

//创建一棵二叉搜索树，返回树的跟节点地置
BstRoot* CreateBst(int arr[],int len);

//中序遍历搜索树
int Search_Bst(BstRoot *Root);

//删除节点
int DeleteNode(BstRoot **Root,int data);

//销毁树
int DestoryBst(BstRoot *Root);

2. 二叉搜索树的源文件  BST.cpp

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
#include"BST.h"

//创建一棵二叉搜索树，返回根节点的地置
BstRoot* CreateBst(int arr[],int len) //给定一个整型数组，和长度，使用数组中的数据创建一棵二叉搜索树
{
	int ret = 0;
	if(arr == NULL) 
	{
		printf("CreateBst Error : BstNode* CreateBst() n");
		return NULL;
	}
	BstNode *Root = new BstNode(arr[0]);	
	for(int i = 1; i < len; i++)
	{
		ret = InsertNode(Root,arr[i]);
		if(ret != 0)
		{
			printf("Insert Data Error : InsertNode() n");
			break;
		}
	}
	return (BstRoot*)Root;
}

//插入数据
int InsertNode(BstRoot *Root,int data)
{
	int ret = 0;
	if(Root == NULL) 
	{
		printf("Parameters Null ：InsertNode() n");
		ret = -1;
		return ret;
	}
	BstNode *root = (BstNode *)Root;

	BstNode *TempNode = new BstNode(data);
	
	while(1)
	{
		if(data < root->val) //如果待插入的数据 < 当前节点数据,往左遍历
		{
			if(root->left == NULL)
			{
				root->left = TempNode;
				break;
			}
			else if(data > root->left->val) //待插入数据 > 当前节点数据下一个的左数据
			{
				TempNode->left = root->left;
				root->left = TempNode;
				break;
			}
			root = root->left;
		}

		else if(data > root->val) //如果待插入的数据 > 当前节点数据,往右遍历
		{
			if(root->right == NULL)
			{
				root->right = TempNode;
				break;
			}
			else if(data < root->right->val)
			{
				TempNode->right = root->right;
				root->right = TempNode;
				break;
			}
			root = root->right;
		}
			
		else //如果相等，则作为左子树
		{
			if(root->left == NULL) root->left = TempNode;
			else
			{
				TempNode->left = root->left;
				root->left = TempNode;
			}
			break;
		}
	}
	return ret;
}

//中序遍历二叉搜索树，打印出节点的属性值
int Search_Bst(BstRoot *Root)
{
	int ret = 0;
	if(Root == NULL)
	{
		ret = -1;
		return ret;
	}
	BstNode *root = (BstNode *)Root;

	//中序遍历树，打印出节点属性值
	Search_Bst(root->left);

	printf("%d ",root->val);

	Search_Bst(root->right);

	return ret;
}

//删除节点属性值为data的节点,删除稍微复杂一点
/*
	当删除某一个节点时：用这个节点的右孩子代替当前节点，然后把这个节点的左孩子，接在右孩子的最左边节点上，因为右孩子的属性值总是>=左孩子的属性，
	因此某一个节点的左孩子节点属性值，肯定小于等于该节点右孩子的最左边节点的属性值。

	当删除的是根节点，我们要改变根节点的值，因此我们需要传出新的根节点的地置

	同时，我们还要判断，一个给定的待删除数是否存在于二叉搜索树中，如果不存在，我们要提示
*/
int DeleteNode(BstRoot **Root,int data)
{
	int ret = 0;
	int tag = 0;
	if(Root == NULL)
	{
		ret = -1;
		printf("Parameters error : DeleteNode(BstRoot *Root,int data) n");
		return ret;
	}
	BstNode *root = *((BstNode **)Root);
	BstNode *temp;
	BstNode *temp1;
	if(data == root->val)  //如果带删除的元素是树的根节点，需要把新的根节点地置传出去
	{
		if( (root->left != NULL) && (root->right != NULL) ) //待删除节点的左右孩子都存在
		{
			temp = root->right;
			while(1)
			{
				if(temp->left != NULL) temp = temp->left;
				else break;
			}
			temp->left = root->left;
			*((BstNode **)Root) = root->right;
		}
		//待删除节点的左右孩子都不存在
		else if((root->left == NULL) && (root->right == NULL)) *((BstNode **)Root) = NULL;

		//待删除节点的左孩子不存在
		else if(root->left == NULL) *((BstNode **)Root) = root->right;

		//待删除节点的右孩子不存在
		else if(root->right == NULL) *((BstNode **)Root) = root->left;
	}
	else //待删除的节点不是根节点，则不需要改变根节点的地置
	{
		while(1)
		{
			if(data < root->val) //如果待删除数 < 当前节点的属性值，往左子树找
			{
				if(root->left == NULL)
					break;
				else if(data == root->left->val) //下一个节点的左节点的属性值 = 待删除的值
				{
					if( (root->left->left != NULL) && (root->left->right != NULL) ) //待删除节点的左右孩子都存在
					{
						temp = root->left;
						root->left = root->left->right;
						temp1 = temp->right;
						while(1)
						{
							if(temp1->left != NULL) temp1 = temp1->left;
							else break;
						}
						temp1->left = temp->left;
					}
					//待删除节点的左右孩子都不存在
					else if( (root->left->left == NULL) && (root->left->right == NULL) )  root->left = NULL;
					//待删除节点的右孩子不存在
					else if(root->left->right == NULL) root->left = root->left->left;
					//待删除节点的左孩子不存在
					else if(root->left->left == NULL) root->left = root->left->right;
					tag = 1;
					break;
				}
				root = root->left;
			}
			else if(data > root->val) //如果待删除数 > 当前节点的属性值，往右子树找
			{
				if(root->right == NULL)
					break;
				else if(data == root->right->val)
				{
					if( (root->right->left != NULL) && (root->right->right != NULL) ) //待删除节点的左右孩子都存在
					{
						temp = root->right;
						root->right = root->right->right;
						temp1 = temp->right;
						while(1)
						{
							if(temp1->left != NULL) temp1 = temp1->left;
							else break;
						}
						temp1->left = temp->left;
					}
					//待删除节点的左右孩子都不存在
					else if((root->right->left == NULL) && (root->right->right == NULL)) root->right = NULL;
					//待删除节点的右孩子不存在
					else if(root->right->right == NULL) root->right = root->right->left;
					//待删除节点的左孩子不存在
					else if(root->right->left == NULL) root->right = root->right->right;
					tag = 1;
					break;
				}
				root = root->right;
			}
		}
		if(tag == 0) printf("二叉搜索树里找不到待删除的元素 n");
   }
   return ret;
}

//销毁一个二叉树搜索树，采取后序遍历
int DestoryBst(BstRoot *Root)
{
	int ret = 0;
	if(Root == NULL)
	{
		ret = -1;
		return ret;
	}
	BstNode *root = (BstNode *)Root;

	DestoryBst(root->left);

	DestoryBst(root->right);

	delete root;

	return ret;
}

3.二叉搜索树的测试源文件Main.cpp

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<stdio.h>
#include<iostream>
#include"BST.h"
int main(int argc, int *argv[])
{
	int a[] = {6,5,3,7,5,8,1,9};
	int ret = 0;

	//测试创建树
	BstRoot *root = CreateBst(a,8);

	//搜索树
	ret = Search_Bst(root);
	printf("n");
	if(ret != 0) printf("Search_Bst() error n");

	//测试插入数据
	ret = InsertNode(root,0);

	ret = Search_Bst(root);
	printf("n");
	if(ret != 0) printf("Search_Bst() error n");

	//测试删除树的头结点
	DeleteNode(&root,6);

	//测试删除树中重复的元素，只删除第一个与待删除数据相等的元素
	DeleteNode(&root,5);
	ret = Search_Bst(root);
	printf("n");
	if(ret != 0) printf("Search_Bst() error n");

	//删除后，再插入
	ret = InsertNode(root,6);
	ret = Search_Bst(root);
	printf("n");
	if(ret != 0) printf("Search_Bst() error n");

	//销毁树
	ret = DestoryBst(root);

	//检查销毁之后树是否存在
	printf(" = %d n",((BstNode *)root)->val);
	printf(" = %d n",((BstNode *)root)->left);
	printf(" = %d n",((BstNode *)root)->right);

	system("pause");
	return 0;
}

 

最后

以上就是清爽大神最近收集整理的关于二叉搜索树基本原理与C语言实现的全部内容，更多相关二叉搜索树基本原理与C语言实现内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(75)

相关文章

C语言？c++？到底先学哪个才能更好的理解编程，这些你造吗
C语言？c++？到底先学哪个才能更好的理解编程，这些你造吗
C语言编写程序（输出最大值+转换变量值+大小写转换+反序数）
C语言编写程序（输出最大值+转换变量值+大小写转换+反序数）
初识c语言
初识c语言
C语言---二叉树(详解)---数据结构
C语言---二叉树(详解)---数据结构
二叉搜索树基本原理与C语言实现
二叉搜索树基本原理与C语言实现
C语言实现二叉树C语言实现二叉树
C语言实现二叉树C语言实现二叉树
C语言数据结构之树超全详解基础知识操作部分树和森林赫夫曼树及其应用
C语言数据结构之树超全详解基础知识操作部分树和森林赫夫曼树及其应用
数据结构--C语言实现链式二叉树--详解二叉树基本知识二叉树基本操作
数据结构--C语言实现链式二叉树--详解二叉树基本知识二叉树基本操作

评论列表共有 0 条评论

立即
投稿
返回
顶部