C语言---二叉树(详解)---数据结构

71 阅读 0 评论 47 点赞

我是靠谱客的博主爱笑短靴，最近开发中收集的这篇文章主要介绍C语言---二叉树(详解)---数据结构，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

树的基本知识点

节点的度：节点拥有的子树的数目。

叶子：度为零的节点。

分支节点：度不为零的节点。

树的度：树中节点的最大的度。

层次：根节点的层次为1，其余节点的层次等于该节点的双亲节点加1。

树的高度：树中节点的最大层次

前序遍历：根结点 ---> 左子树 ---> 右子树

中序遍历：左子树---> 根结点 ---> 右子树

后序遍历：左子树 ---> 右子树 ---> 根结点

首先需要知道上面的知识点，才能对树有一些认知。

那么写树，就是写树的遍历

写二叉树需要创建一个结构体，还有重定义类型

因为是有节点的，而每个节点都需要我们自己去申请空间，所以我们先把节点都创建出来

然后把你自己规划的树写出来

如:

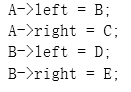
那么在图片中是这样的

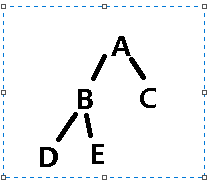
1.前序遍历

每次进去，我们都先判断当前的节点是否为空，如果为空，我们打印NULL。并且进入下一次递归(前，中，后序遍历都用遍历)

然后我们依次根结点 ---> 左子树 ---> 右子树

然后依次遍历

接下来都是一样的，只不过顺序变了

2.中序遍历

3.后序遍历

4.计算树的叶子节点个数

分三种情况，1.树中没有节点，2.树中只存在一个节点。3.树中有n个节点

5.计算树中的叶子节点

我们去依次遍历左，右节点，最后加起来（这里要+1是因为要把刚开始的节点加进去，才算所有节点)

树难的不是代码，而是你要去理解树的作用和树的知识点，能理解，那么代码写的会更加轻松

接下来是代码段

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

typedef char STDatype;

typedef struct BinartTreeNode
{
	struct BinartTreeNode* left;//指向左节点的指针
	struct BinartTreeNode* right;//指向右节点的指针
	STDatype data;//存放数据
}BTNode;




int TreeLeafSize1(BTNode* root)
{
	if (root == NULL)//若树没有节点 则返回0
		return 0;
	if (root->left == NULL && root->right == NULL)//若第一个节点的左丶右都没有节点，则只有第一个节点，那么就返回一个
		return 1;
	return TreeLeafSize1(root->left) + TreeLeafSize1(root->right);//一直遍历都已经没有下一个左右节点了，那么该节点就是叶子节点，再把他们加起来
}

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

void PrevOrder(BTNode* root)
{
	//printf("前序n");
	if (root == NULL)
	{
		printf("NULL->");
		return;
	}
	printf("%c->", root->data);//
	PrevOrder(root->left);
	PrevOrder(root->right);
	//printf("n");
}

void InOrder(BTNode* root)
{
	//printf("中序n");
	if (root == NULL)
	{
		printf("NULL->");
		return;
	}
	InOrder(root->left);
	printf("%c->", root->data);
	InOrder(root->right);
	//printf("n");
}

void PostOrder(BTNode* root)
{
	//printf("后序n");
	if (root == NULL)
	{
		printf("NULL->");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c->", root->data);
	//printf("n");
}



void Intenode()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;

	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;

	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;

	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;

	// 前序 中序 后序遍历
	//void PrevOrder(BTNode* root)
	printf("前序n");
	PrevOrder(A);
	printf("n");
	printf("中序n");
	//void InOrder(BTNode* root)
	InOrder(A);
	printf("n");
	//void PostOrder(BTNode* root)
	printf("后序n");
	PostOrder(A);
	printf("n");
	 节点个数
	//int TreeSize(BTNode* root)
	int number=TreeSize(A);
	printf("节点个数有:%dn", number);
	 叶子节点的个数
	//int TreeLeafSize(BTNode* root)
	int number1=TreeLeafSize1(A);
	printf("叶子节点个数有:%dn", number1);
	 层序遍历
	//void LevelOrder(BTNode* root)
	/*LevelOrder(A);*/
}

int main()
{
	Intenode();

	return 0;
}