概述
这些天复习了排序这个模块，排序算法在程序员的日常工作中是必不可少的，有时候我们不知不觉就用到了排序，这是因为高级语言系统已经比较完美的封装和优化了排序算法，并且在笔试，面试等方面我们都能见到它的身影。下面结合那本大三的教材：严版的《数据结构》，来说一说这几个经典的排序算法，如果有不对的欢迎指正！
首先我们还是先说基础概念（按书上说的），万变离不开概念，没有概念没有规矩，那可不行。
一、冒泡排序
二、直接选择排序
三、直接插入排序
四、希尔排序
五、堆排序
六、归并排序
七、快速排序
八、各种算法效率比拼
1：内部排序和外部排序（我们重点说内部排序（因为我们最常用到））
内排序：在排序的时间数据对象全部存放在内存的排序。
外排序：在排序的时间对象个数太多，不能同时存放在内存，根据排序的要求，不断在内、外存之间移动。
2：排序的方法
按所排列（移动交换）的方式不同，可归纳为五类：插入排序、选择排序、交换排序、归并排序和分配排序（有的书上直接说基数）。
插入排序主要包括直接插入排序和希尔排序两种；
选择排序主要包括直接选择排序和堆排序；
交换排序主要包括冒泡排序和快速排序；
归并排序主要包括二路归并（常用的归并排序）。
分配排序主要包括箱排序和基数排序。
3：稳定性
稳定排序：假设在待排序的文件中，存在两个或两个以上的记录具有相同的关键字，在用某种排序法排序后，若这些相同关键字的元素的相对次序仍然不变，则这种排序方法是稳定的。
冒泡，插入，基数，归并属于稳定排序；
选择，快速，希尔，堆属于不稳定排序。
4：图表帮助大家记忆：
| 各种排序算法 | |||||
| 类别 | 排序方法 | 时间复杂度 | 稳定性 | ||
| 平均情况 | 最好情况 | 最坏情况 | |||
| 插入排序 | 直接插入 | O(n2) | O(n) | O(n2) | 稳定 |
| 希尔排序 | O(n1.3) | O(n) | O(n2) | 不稳定 | |
| 选择排序 | 直接选择 | O(n2) | O(n2) | O(n2) | 不稳定 |
| 堆排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | 不稳定 | |
| 交换排序 | 冒泡排序 | O(n2) | O(n) | O(n2) | 稳定 |
| 快速排序 | O(nlog2n) | O(nlog2n) | O(n2) | 不稳定 | |
| 归并排序 | O(nlog2n) | O(nlog2n) | O(nlog2n) | 稳定 | |
| 基数排序 | O(d(r+n)) | O(d(n+rd)) | O(d(r+n)) | 稳定 | |
一、冒泡排序
冒泡排序也叫起泡排序，大家都知道，学C语言那会的循环结构就那这个做的例子，冒泡排序过程很简单，但是效率太低。
1：简要过程：
首先将一个记录的关键字和第二个记录的关键字比较若为逆序将两个记录交换，然后比较第二个记录和第三个记录的关键字....,直到n-1个记录呢第n个记录的关键字进行比较，上述过称作一趟冒泡排序，然后进行第二趟，对n-1个记录进行操作...（可以不安这种方法来，实际应用中可以逆序也可以正序）
2：排序效率：
如果开始的时候需要排序的元素是正序，则只要一趟，需要n-1次的关键字比较，如果为逆序要进行n(n-1)/2次的比较，所以时间复杂度是O(n2)，所以效率超级的低，一般不建议使用
3：排序过程图：
4：具体算法实现（可以有多种形式）：
1 //冒泡排序 2 void bubbling(int arr[], int n){ 3 int i, j, temp; 4 for (j = 0; j < n - 1; j++){ 5 for (i = 0; i < n - 1 - j; i++){ 6 if(arr[i] > arr[i + 1]){ 7 temp = arr[i]; 8 arr[i] = arr[i + 1]; 9 arr[i + 1] = temp; 10 } 11 } 12 } 13 }
二、直接选择排序
是一种选择排序，总的来说交换的少，比较的多，如果排序的数据是字符串的话比建议使用这种方法。
1：简要过程：
首先找出最大元素，与最后一个元素交换（arr[n-1]），然后再剩下的元素中找最大元素，与倒数第二个元素交换....直到排序完成。
2：排序效率：
一趟排序通过n-1次的关键字比较，从n-i-1个记录中选择最大或者最小的元素并和第i个元素交换，所以平均为n(n-1)/2，时间复杂度为O(n2)，也不是个省油的灯，效率还是比较低。
3：排序过程图：（选择小元素，图片来源百度搜索）
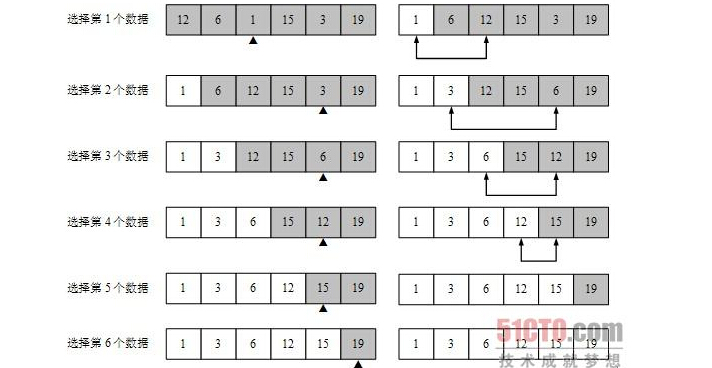
4：具体算法实现：
1 //直接选择排序
2 void directDialing(int arr[], int n){
3
int i,j,k,num;
4
for(i = 0; i < n; i++){
5
num = 0;
6
for(j = 0; j < n-i; j++){
7
if(arr[j] > arr[num]){
8
num = j;
9
}
10
}
11
k = arr[n-i-1];
12
arr[n-i-1] = arr[num];
13
arr[num] = k;
14
}
15 }
三、直接插入排序
是一种简单的排序方法，算法简洁，容易实现
1：简要过程：
每步将一个待排序元素，插入到前面已经排序好的元素中，从而得到一个新的有序序列，直到最后一个元素加入进去即可。
2：排序效率：
空间上直接插入排序只需要一个辅助空间，时间上：花在比较两个关键字的大小和移动记录，逆序时比较次数最大：（n+2）(n-1)/2，平均：n2/4，所以直接插入排序时间复杂度也是O(n2)
3：排序过程图：
4：具体算法实现：
1 //直接插入排序
2 void
insert(int arr[], int n){
3
int m,i,k;
4
for(i = 1; i < n; i++){
5
m = arr[i];
6
for(k = i-1; k >= 0; k--){
7
if(arr[k] > m){
8
arr[k+1] = arr[k];
9
}else{
10
break;
11
}
12
}
13
arr[k+1] = m;
14
}
15 }
四、希尔排序
希尔排序，也叫缩小增量排序，是一种插入排序，和前三种不一样它在时间效率上有很大的改进，所以这种排序方法才是我们需要重点学习和掌握的，但是凡事都有利弊，容易的排序算法算法简单，但是效率低下，反过来复杂的排序算法算法复杂，但是效率及其的出色。
1：简要过程：
选择一个增量序列a1，a2，…，ak，其中ai>aj，ak=1；按增量序列个数k，对序列进行k 趟排序；每趟排序，根据对应的增量ai，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
说白了其实就是：先取一个正整数d1<n，把所有序号相隔d1的数组元素放一组，组内进行直接插入排序；然后取d2<d1，重复上述分组和排序操作；直至di=1，即所有记录放进一个组中排序为止。
2：排序效率：
希尔排序的效率的确不低，大量的研究说时间复杂度为O(n3/2)（书上说的在大量的试验基础上推出的）感觉有点玄乎，但是希尔排序效率确实很高，在后面我写的有一个效率比拼大家可以看看。
3：排序过程图：
4：具体算法实现：
1 //希尔排序
2 void Heer(int arr[], int n){
3
int i,j,k,num;
4
k = n/2;
5
while(k > 0){
6
for(i = k; i < n; i++){
7
num = arr[i];
8
for(j = i - k;j >= 0; j -= k){
9
if(arr[j] > num){
10
arr[j+k] = arr[j];
11
}else{
12
break;
13
}
14
}
15
arr[j+k] = num;
16
}
17
k = k/2;
18
}
19 }
五、堆排序
先说说堆的定义：n个元素的序列{k1,k2,. . . kn}当且仅当满足以下条件时称之为堆：
ki <= k2i ki >= k2i
ki <= k2i+1 ki >= k2i+1
若将这样的序列对用的一维数组看成一个完全二叉树则堆的定义看出：完全二叉树非终节点的值均不大于（不小于）其左右两个孩子的节点值。
大顶堆和小顶堆：堆顶元素取最小值的是小顶堆，取最大值的是大顶堆。
1：简要过程：
(1) 建堆：对初始序列建堆的过程，就是一个反复进行筛选的过程。n 个结点的完全二叉树，则最后一个结点是第
（既是程序中的n * 2 +1）个结点的子树。筛选从第个结点为根的子树开始，该子树成为堆。之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。
(2) 调整堆：k个元素的堆，输出堆顶元素后，剩下k-1 个元素。将堆底元素送入堆顶（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。将根结点与左、右子树中较小元素的进行交换。若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复调整堆，.若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复调整堆。对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。
2：排序效率：
堆排序的方法对记录较少的文件并不值得提倡，但对于数据较大的文件还是很有效的，时间主要花在初始建堆和交换元素后调整堆上。对深度为k的堆比较算法最多为2（k-1）次，含有n个元素深度为h的堆时总共进行的关键字比较不超过4n，由此可见最坏的情况下，时间复杂度为O(nlogn)并且仅需要一个辅助控间，速度已经是相当快了。
3：排序过程图（图片来源百度，帮助理解）：
4：具体算法实现：
1 //堆调整
2 void adjust(int arr[], int n, int length){
3
int max,b;
4
while(n * 2 +1 <= length){//说明存在左节点
5
max = n * 2 + 1;
6
if(n * 2 + 2 <= length){//说明存在右节点
7
if(arr[max] < arr[n * 2 + 2]){
8
max = n * 2 + 2; //跟新最小的值
9
}
10
}
11
if(arr[n] > arr[max]){
12
break;//顺序正确，不需要再调整
13
}else{
14
b = arr[n];
15
arr[n] = arr[max];
16
arr[max] = b;
17
n = max;
18
}
19
}
20 }
21
22 //堆排序
23 void stack(int arr[], int length){
24
int i,k,m = 0;
25
for(i = length/2-1; i >=0; i--){
26
adjust(arr,i,length-1);
27
}
28
//调整堆
29
for(i = length-1 ;i >= 0; i--){
30
//调整后把最后一个和第一个交换，每次调整少一个元素，依次向前
31
k = arr[i];
32
arr[i] = arr[0];
33
arr[0] = k;
34
adjust(arr,0,i-1);
35
}
36 }
六、归并排序
将两个和两个以上的排序表合成一个新的有序表，归并排序是分治法思想运用的一个典范。
1：简要过程：
将有 n个对象的原始序 列看作 n个有序子列，每个序列的长度为1，从第一个子序列开始，把相邻的子序列两两合并得到[n/2]个长度为2或者是1的归并项，（如果n为奇数，则最后一个有序子序列的长度为1），称这一个过程为一趟归并排序。
然后重复上述过程指导得到一个长度为n的序列为止。
2：排序效率：
一趟归并排序的操作是：调用[n/2b]次算法，整个过程需要[log2n]趟，课件归并排序时间复杂度是O(logn)
3：排序过程图：
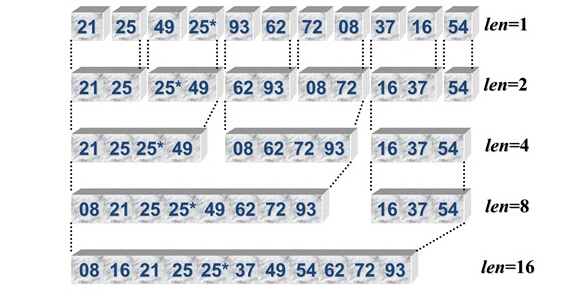
4：具体算法实现：
1 //归并排序合并函数
2 void mergeSoft(int a[], int first, int mid, int last, int temp[]){
3
int i = first, j = mid + 1;
4
int m = mid,
n = last;
5
int k = 0;
6
while (i <= m && j <= n){
7
if (a[i] <= a[j]){
8
temp[k++] = a[i++];
9
}else{
10
temp[k++] = a[j++];
11
}
12
}
13
while (i <= m){
14
temp[k++] = a[i++];
15
}
16
while (j <= n){
17
temp[k++] = a[j++];
18
}
19
20
for (i = 0; i < k; i++){
21
a[first + i] = temp[i];
22
}
23 }
24
25 //归并排序递归拆分函数
26 void mergerSelf(int arr[], int left, int right, int arrTmp[]){
27
if(left < right){
28
int center = (left + right)/2;
29
mergerSelf(arr, left, center, arrTmp);
30
mergerSelf(arr, center+1, right, arrTmp);
31
mergeSoft(arr, left, center, right, arrTmp);
32
}
33 }
34 //归并排序
35 void merger(int arr[], int n){
36
int *arrTmp = new int[n];
37
mergerSelf(arr, 0, n - 1, arrTmp);
38
delete[] arrTmp;
39 }
七、快速排序
快速排序是一种交换排序，说白了就是一种对起泡排序的改进，不过改进了不少，快速排序被认为是最好的一种排序算法（同量级别）。
1：简要过程：
选择一个基准元素，我们称之为中枢，通常选择第一个元素或者最后一个元素，中枢的选择很重要，直接影响排序的性能，这是因为如果代排序列有序，快速排序就退化为冒泡排序。将序列分割成左右两个序列。其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。一趟排序的具体做法将两个附设指针left和right，然后分别对这两部分记录用同样的方法继续进行排序，直到整个序列有序。
2：排序效率：
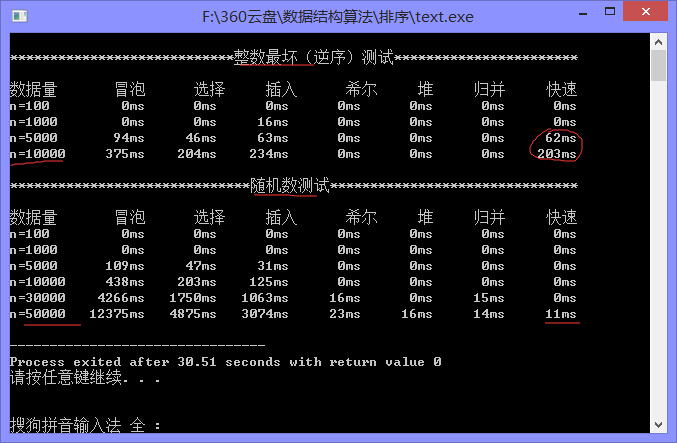
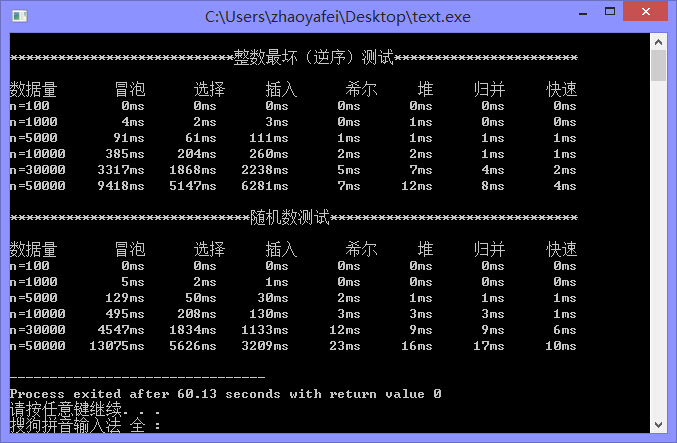
在所有同级别的排序算法中其平均性能最好O(nlogn)。如果代排序列有序，快速排序就退化为冒泡排序，效率及其低下，这个可以在下面的效率比拼图中体现出来逆序的时候快速排序非常慢，效率很低下。所以可以在中枢的选择上优化可以选着最左边和最右边中间的元素取其平均值即可。
3：排序过程图：
4：具体算法实现：
1 //快速排序的元素移动
2 int fastSort(int arr[], int left, int right){
3
int center = (left+right)/2;
4
int num = arr[center]; //记录中枢点的位置，这里选择最左边点当做中枢点
5
while(left < right){
6
//比枢纽小的移动到左边
7
while(left < right && arr[right] >= num){
8
right--; //一直到有一个元素小于所选关键中枢为止
9
}
10
arr[left] = arr[right];
11
12
while(left < right && arr[left] <= num){
13
left++; //一直到有一个元素大于所选关键中枢为止
14
}
15
arr[right] = arr[left]; //关键字入列
16
}
17
arr[left] = num;
18
return left;
19 }
20
21 //快速排序递归划分
22 int fastSortSelf(int arr[], int left, int right){
23
if(left < right){
24
int lowLocation = fastSort(arr,left,right); //第一个指针的位置
25
fastSortSelf(arr,left,lowLocation - 1);
26
fastSortSelf(arr,lowLocation + 1,right);
27
}
28 }
29
30 //快速排序
31 void fast(int arr[], int n){
32
fastSortSelf(arr,0,n-1);
33
//记录时间
34 }
八、各种算法效率比拼
下面是我自己写的一个算法比拼，测试数据有100-50000都有，分为最坏情况（逆序->正序）和随机情况（随机->正序），测试数据会因为机器的不同而不同，我的是win8，64, 4G，cpu2.5，欢迎大家测试
说明两点：要注意时间的得到方法，需要引入的头文件包括
1 #include <iostream>
2 #include <iomanip>
3 #include <stdlib.h>
4 #include <time.h>
1 end_time = clock(); 2 程序。。。。 3 times = static_cast<double>(end_timestart_time)/CLOCKS_PER_SEC*1000;cout <<right ; cout <<setw(7) <<times<<"ms";
下面是程序代码：
1 #include <iostream>
2 #include <iomanip>
3 #include <stdlib.h>
4 #include <time.h>
5 using namespace std;
6
7 clock_t start_time, end_time;
8 int times;
9
10 void printfArr(int arr[], int n){
11
for(int i = 0; i < n; i++){
12
cout<<arr[i]<<" ";
13
}
14 }
15
16 //冒泡排序
17 void bubbling(int arr[], int n){
18
start_time = clock();
19
int i, j, temp;
20
for (j = 0; j < n - 1; j++){
21
for (i = 0; i < n - 1 - j; i++){
22
if(arr[i] > arr[i + 1]){
23
temp = arr[i];
24
arr[i] = arr[i + 1];
25
arr[i + 1] = temp;
26
}
27
}
28
}
29
end_time = clock();
30
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
31
cout <<right ; cout <<setw(7) <<times<<"ms";
32 }
33
34 //直接选择排序
35 void directDialing(int arr[], int n){
36
start_time = clock();
37
int i,j,k,num;
38
for(i = 0; i < n; i++){
39
num = 0;
40
for(j = 0; j < n-i; j++){
41
if(arr[j] > arr[num]){
42
num = j;
43
}
44
}
45
k = arr[n-i-1];
46
arr[n-i-1] = arr[num];
47
arr[num] = k;
48
}
49
end_time = clock();
50
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
51
cout <<right ; cout <<setw(7) <<times<<"ms";
52 }
53
54 //直接插入排序 (On2)
55 void
insert(int arr[], int n){
56
start_time = clock();
57
int m,i,k;
58
for(i = 1; i < n; i++){
59
m = arr[i];
60
for(k = i-1; k >= 0; k--){
61
if(arr[k] > m){
62
arr[k+1] = arr[k];
63
}else{
64
break;
65
}
66
}
67
arr[k+1] = m;
68
}
69
end_time = clock();
70
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
71
cout <<right ; cout <<setw(7) <<times<<"ms";
72 }
73
74 //希尔排序
75 void Heer(int arr[], int n){
76
start_time = clock();
77
int i,j,k,num;
78
k = n/2;
79
while(k > 0){
80
for(i = k; i < n; i++){
81
num = arr[i];
82
for(j = i - k;j >= 0; j -= k){
83
if(arr[j] > num){
84
arr[j+k] = arr[j];
85
}else{
86
break;
87
}
88
}
89
arr[j+k] = num;
90
}
91
k = k/2;
92
}
93
end_time = clock();
94
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
95
cout <<right ; cout <<setw(7) <<times<<"ms";
96 }
97
98 //堆调整
99 void adjust(int arr[], int n, int length){
100
int max,b;
101
while(n * 2 +1 <= length){//说明存在左节点
102
max = n * 2 + 1;
103
if(n * 2 + 2 <= length){//说明存在右节点
104
if(arr[max] < arr[n * 2 + 2]){
105
max = n * 2 + 2; //跟新最小的值
106
}
107
}
108
if(arr[n] > arr[max]){
109
break;//顺序正确，不需要再调整
110
}else{
111
b = arr[n];
112
arr[n] = arr[max];
113
arr[max] = b;
114
n = max;
115
}
116
}
117 }
118
119 //堆排序
120 void stack(int arr[], int length){
121
start_time = clock();
122
int i,k,m = 0;
123
for(i = length/2-1; i >=0; i--){
124
adjust(arr,i,length-1);
125
}
126
//调整堆
127
for(i = length-1 ;i >= 0; i--){
128
//调整后把最后一个和第一个交换，每次调整少一个元素，依次向前
129
k = arr[i];
130
arr[i] = arr[0];
131
arr[0] = k;
132
adjust(arr,0,i-1);
133
}
134
end_time = clock();
135
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
136
cout <<right ; cout <<setw(7) <<times<<"ms";
137 }
138
139 //归并排序合并函数
140 void mergeSoft(int a[], int first, int mid, int last, int temp[]){
141
int i = first, j = mid + 1;
142
int m = mid,
n = last;
143
int k = 0;
144
while (i <= m && j <= n){
145
if (a[i] <= a[j]){
146
temp[k++] = a[i++];
147
}else{
148
temp[k++] = a[j++];
149
}
150
}
151
while (i <= m){
152
temp[k++] = a[i++];
153
}
154
while (j <= n){
155
temp[k++] = a[j++];
156
}
157
158
for (i = 0; i < k; i++){
159
a[first + i] = temp[i];
160
}
161 }
162
163 //归并排序递归拆分函数
164 void mergerSelf(int arr[], int left, int right, int arrTmp[]){
165
if(left < right){
166
int center = (left + right)/2;
167
mergerSelf(arr, left, center, arrTmp);
168
mergerSelf(arr, center+1, right, arrTmp);
169
mergeSoft(arr, left, center, right, arrTmp);
170
}
171 }
172 //归并排序
173 void merger(int arr[], int n){
174
start_time = clock();
175
int *arrTmp = new int[n];
176
mergerSelf(arr, 0, n - 1, arrTmp);
177
delete[] arrTmp;
178
//记录时间
179
end_time = clock();
180
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
181
cout <<right ; cout <<setw(7) <<times<<"ms";
182 }
183
184 //快速排序的元素移动
185 int fastSort(int arr[], int left, int right){
186
int center = (left+right)/2;
187
int num = arr[center]; //记录中枢点的位置，这里选择最左边点当做中枢点
188
while(left < right){
189
//比枢纽小的移动到左边
190
while(left < right && arr[right] >= num){
191
right--; //一直到有一个元素小于所选关键中枢为止
192
}
193
arr[left] = arr[right];
194
195
while(left < right && arr[left] <= num){
196
left++; //一直到有一个元素大于所选关键中枢为止
197
}
198
arr[right] = arr[left]; //关键字入列
199
}
200
arr[left] = num;
201
return left;
202 }
203
204 //快速排序递归划分
205 int fastSortSelf(int arr[], int left, int right){
206
if(left < right){
207
int lowLocation = fastSort(arr,left,right); //第一个指针的位置
208
fastSortSelf(arr,left,lowLocation - 1);
209
fastSortSelf(arr,lowLocation + 1,right);
210
}
211 }
212
213 //快速排序
214 void fast(int arr[], int n){
215
start_time = clock();
216
fastSortSelf(arr,0,n-1);
217
//记录时间
218
end_time = clock();
219
times = static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000;
220
cout <<right ; cout <<setw(7) <<times<<"ms";
221 }
222
223 int main(){
224
cout<<"n****************************整数最坏（逆序）测试***********************nn";
225
cout<<"数据量
冒泡
选择
插入
希尔
堆
归并
快速n";
226
int size;
//记录每个测试数量
227
int tmpNum; //记录临时数
228
int arr1[8] = {49,38,65,97,76,13,27,49};
229
//测试数据的各个范围
230
int nums[6] = {100,1000,5000,10000,30000,50000};
231
/*
232
printfArr(arr1,8);
233
printf("n");
234
fast(arr1,8);
235
printfArr(arr1,8);*/
236
237
for(int p = 0; p < 6; p++){
238
size = nums[p];
239
int arrs1[size],arrs2[size],arrs3[size],arrs4[size],arrs5[size],arrs6[size],arrs7[size];
240
cout<<left; cout <<"n="<<setw(6)<<size;
241
//产生有序数
242
for(int m = 0; m < size; m++){
243
int tmpNum = size - m;
244
arrs1[m] = tmpNum;
245
arrs2[m] = tmpNum;
246
arrs3[m] = tmpNum;
247
arrs4[m] = tmpNum;
248
arrs5[m] = tmpNum;
249
arrs6[m] = tmpNum;
250
arrs7[m] = tmpNum;
251
}
252
bubbling(arrs1,size);
//冒泡排序法
253
directDialing(arrs2,size);//直接选择排序
254
insert(arrs3,size);
//直接插入排序
255
Heer(arrs4,size);
//希尔排序
256
stack(arrs5,size);
//堆排序
257
merger(arrs6,size);
//归并排序
258
fast(arrs7,size);
//快速排序
259
cout<<"n";
260
}
261
262
//*****************随机数测试法******************
263
int number;
264
int nlong; //数据量
265
cout<<"n******************************随机数测试*******************************nn";
266
cout<<"数据量
冒泡
选择
插入
希尔
堆
归并
快速n";
267
for(int r = 0; r < 6; r++){
268
size = nums[r];
269
int rands1[size],rands2[size],rands3[size],rands4[size],rands5[size],rands6[size],rands7[size];
270
//产生测试随机数
271
srand((unsigned) time(NULL));
272
for (int rd = 0; rd < size; rd++){
273
tmpNum = rand() % size;
274
rands1[rd] = tmpNum;
275
rands2[rd] = tmpNum;
276
rands3[rd] = tmpNum;
277
rands4[rd] = tmpNum;
278
rands5[rd] = tmpNum;
279
rands6[rd] = tmpNum;
280
rands7[rd] = tmpNum;
281
}
282
//输出测试数据量
283
cout<<left; cout <<"n="<<setw(6)<<size;
284
//依次调用各个排序函数
285
bubbling(rands1,size);
//冒泡排序法
286
directDialing(rands2,size);//直接选择排序
287
insert(rands3,size);
//直接插入排序
288
Heer(rands4,size);
//希尔排序
289
stack(rands5,size);
//堆排序
290
merger(rands6,size);
//归并排序
291
fast(rands7,size);
//快速排序
292
cout<<"n";
293
}
294 }
运行结果如图：没有优化快速排序（逆序中枢选择第一个）前的效果，n=30000的时候递归太深出错，只能把n=10000。
运行结果如图：优化后快速排序（逆序中枢选择第一个最后一个的中间值）的效果，n=50000的时候，只用了4ms
因为时间关系，写的不全，比如：算法具体的时间复杂度计算方法没有详细写出（有时间会补充完整），还有就是快速排序的改进程序，归并排序的合并细节没有说。反正是写每个程序都遇到很多问题，所有程序都可以编译运行，希望大家提出宝贵意见。
转载请注明出处！
转载于:https://www.cnblogs.com/zyf-zhaoyafei/p/4658333.html
最后
以上就是着急金针菇为你收集整理的经典的排序算法的全部内容，希望文章能够帮你解决经典的排序算法所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复