LESSON 7
2A-L5 Edge detection: Gradients
0.Intro
上一节我们讲述了模板匹配,我们有了固定大小的模板,然后去做相关操作,找到模板的位置
但是若我们事先不知道模板什么样子,我们该如何提取信息去找到我们感兴趣的东西呢?
1.Reduced Images

可以看到,尽管这些图片仅仅只是绘制了边缘,但是我们依然知道图片绘制了什么。
我们可以猜测,在图片的边缘中依然有很多信息值得我们分析
但是在分析边缘信息之前,我们先要学会怎么提取边缘信息
我们一般将这种操作称作边缘检测[Edge detection]
顺便说一下, 教授将这种只含有边缘的图片称作reduced images
2.Edges

可以从这张古老的图片看出,有四种常用的边界,从上往下依次是:
- surface normal discontinuity 表面自然不连续
- depth discontinuity 在深度方向上的不连续
- Surface color discontinuity 表面颜色的不连续
- illumination discontinuity 照明导致的不连续

在显示中的照片中也有这几种 discontinuity (可能翻译为边界好一些)
(好吧,笔者感觉目前对边界分类作用不太大)
3.Change Boundaries Quiz

猜猜看,哪个不是shape或者illumination造成的边界?
4.Change Boundaries Quiz Solution
选D
D.标志上的条纹 不是由于形状或者照明(shape 或 illumination)变化引起的
它与反射纹理或反射颜色有关(reflected texture or reflected color)
5.Edge Detection
所以我们的问题变成了,怎样找到边界上的像素点?
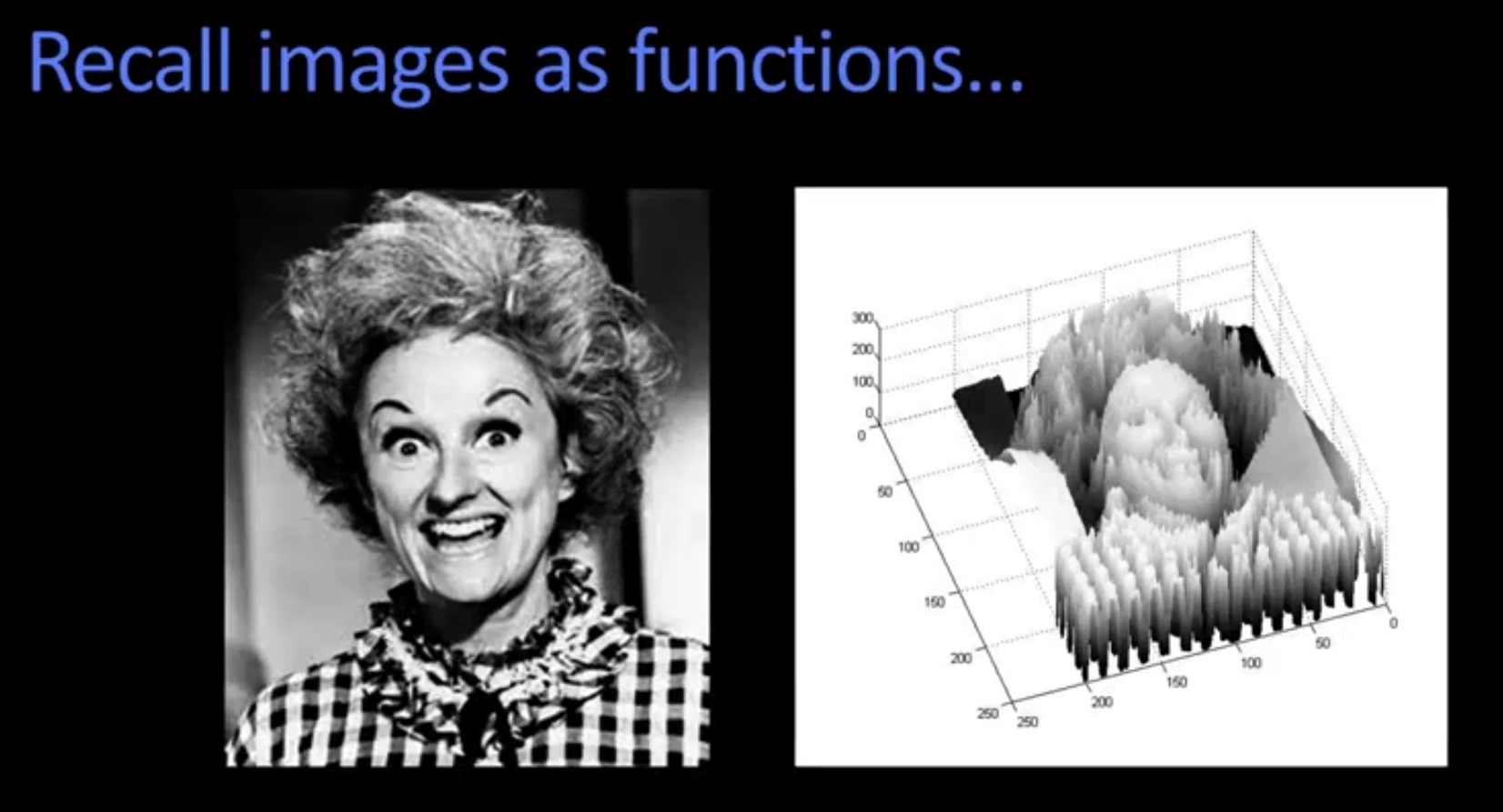
回想一下,我们之前将image视作函数的那张图片,可以看到在边界的地方有很"陡峭的悬崖"
所以我们的问题就变成了,在一个小范围内,找到陡峭的悬崖,此处即是边界,是的,听起来很简单

但是还是有两个问题需要我们考虑:
- 我们要在多小的范围内找到边界
- "悬崖"多高,就是像素的变化值变化多大才能视为边界
同时,我们以没必要找到准确的像素位置,我们只需要将这些80+的数字视为一侧,而20+,30+的数字视为另一侧即可

6.Derivatives and Edges
我们将图片视为函数,那么图片的变化是什么呢?
没错,就是导数,好,那我们来看看导数和边界的关系
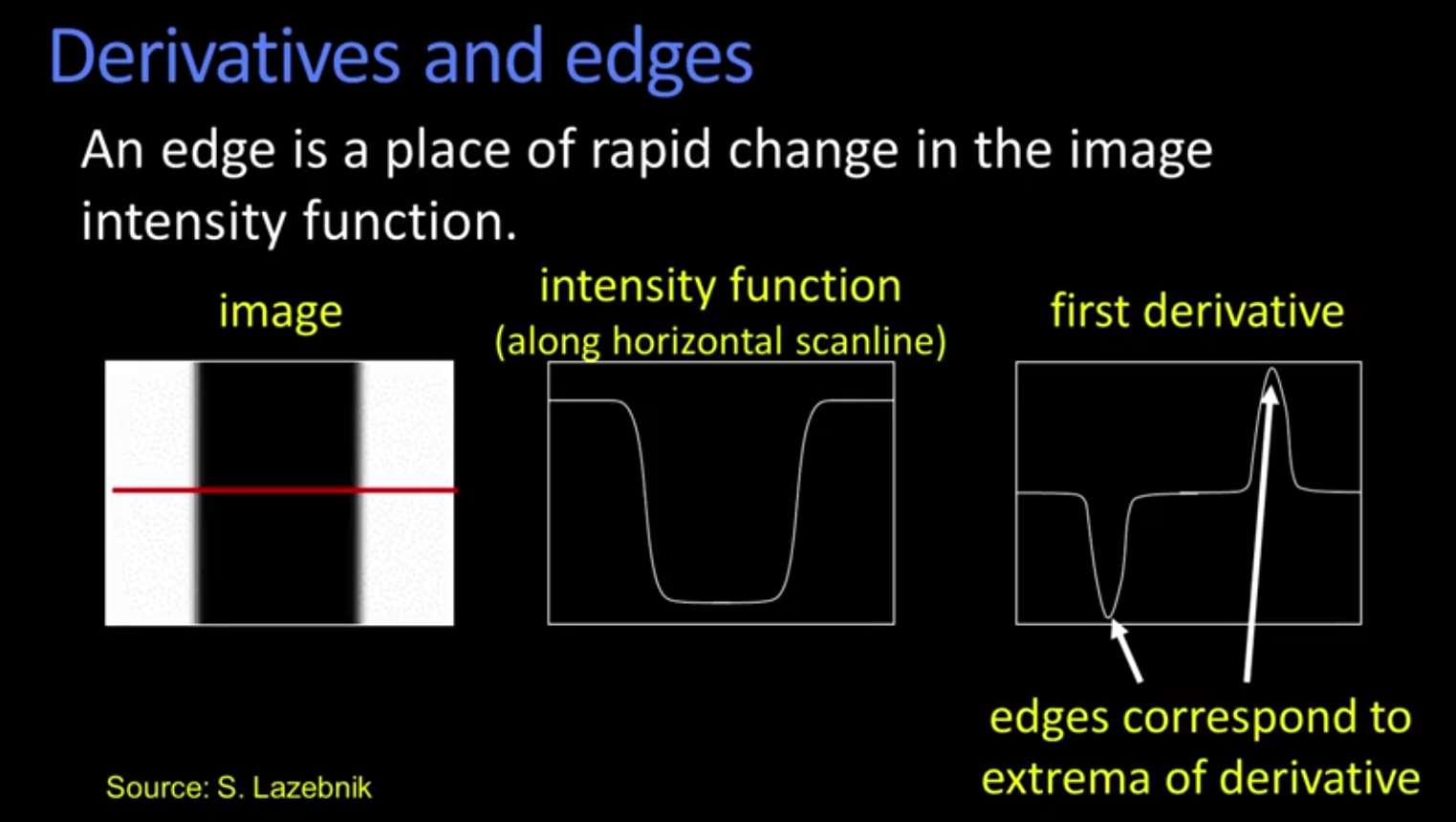
在图中的第一行将边界定义为:图像灰度函数迅速变化的区域就是边界
将左图红线上的灰度值展示在中间的图片上,可以很明显地看到灰度值的走势
对该图像求一阶导数,得到右图,可以看到一阶导数有两个极值
可以猜到,边界与一阶导数的极值有关
那我们现在的问题是,如何找到一阶导数的极值点???
你还记得这位网红吗??我们的waldo

我们当时是怎么做的??滤波!给图像做滤波,然后通过观察滤波后的结果,找到waldo的位置
同理,我们为了找到一阶导数极值的位置,也要对图像做滤波
7.What is a Gradient
我们通过计算图片的梯度,然后给梯度设定阈值需选择我们的边界
(We are going to compute that image gradient function.)
(Then we are going to threshold this gradient function to select the edge pixels)
那么,什么是梯度

回想一下,高中的数学怎么学的,导数的方向是函数值增大的方向还是减小的方向,忘了??
x
2
x^{2}
x2求个导,看看
是的,导数值的方向是函数增大的方向,可以将梯度视为函数导数的推广
将分别对各维度变量求偏导组成的向量可以称为梯度(可能笔者说的不准确,大家都懂就好)
所以梯度方向,是多元函数值增大的方向
忘了说刚刚的图了:
∇
f
=
[
∂
f
∂
x
,
0
]
nabla f = [frac{partial f}{partial x}, 0]
∇f=[∂x∂f,0] 这是仅对
x
x
x方向求偏导
∇
f
=
[
0
,
∂
f
∂
y
]
nabla f = [0, frac{partial f}{partial y}]
∇f=[0,∂y∂f] 这是仅对
y
y
y方向求偏导
∇
f
=
[
∂
f
∂
x
,
∂
f
∂
y
]
nabla f = [frac{partial f}{partial x}, frac{partial f}{partial y}]
∇f=[∂x∂f,∂y∂f] 这是仅对
x
y
xy
xy方向求偏导
嘿嘿,相当于没说
我们再来看看梯度的幅值和方向,和高数中的一样哈

注: 梯度的方向是上式
θ
theta
θ,其为梯度和
x
x
x轴正方向的夹角,同时,
y
y
y轴正方向是朝下的
8.Magnitude Quiz
当梯度的幅值为0时,意味着什么?

9. Magnitude Quiz Solution
根据高中数学,明显为 D
10. Finite Differences
嗯,有限差分,老铁们可能会想到前向差分和后向差分,就不多说了
在连续域内, f ( x , y ) f(x, y) f(x,y)在 x x x方向上的偏微分定义为:
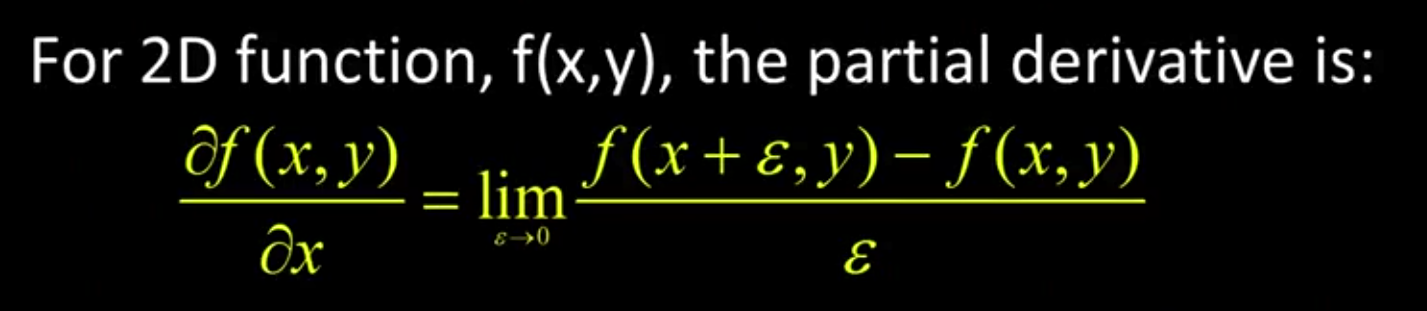
但在离散域内,
f
(
x
,
y
)
f(x, y)
f(x,y)在
x
x
x方向上的偏微分中
ε
varepsilon
ε不能趋于0,只能取1,所以,离散梯度定义为:

下面写着,右向差分,也就是我们常说的前向差分。
我们来猜一下,右图是左图的
x
x
x方向的差分还是
y
y
y方向的差分

我们可以看到:

所以应该是在
x
x
x方向的差分,因为其对水平方向的变化很敏感
11. Finite Differences

第一个问题,下面两张图,哪一个是对
x
x
x求偏导,哪一个是对
y
y
y求偏导
左图垂直方向的轮廓很清楚,所以是对
x
x
x求偏导
右图水平方向的轮廓很清楚,所以是对
y
y
y求偏导

都懂哈,那是相关核,只是在卷积神经网络中那么叫而已

那在
y
y
y方向,我们该选择哪个相关核呢?
这取决于你,若你想
y
y
y的正方向为朝下,那就选择左边的。如果你想正方向朝上,那就选择右边的。
如果你是计算机科学家,多选择左边,若你是数学家,那就选择右边
(想想你高中的笛卡尔坐标系,正方向朝上)

再次放出这只老虎,上边的图是,绘制了梯度的幅值,使用的是如下公式:

Emmmmmm......看起来还算是一张好的边界图吧
12. The Discrete Gradient

上图是导数的定义,但是我们想让滤波器来实现它,我们该怎们做呢?或者说,我们需要什么滤波器呢?

上图左边的滤波器看上去不错,但是它缺少中间像素,这样的话,求出来的梯度是属于左边的像素点呢?还是右边的像素点呢?
而右边的相关核相对较好一点儿,但是为什么会出现连个二分之一呢??
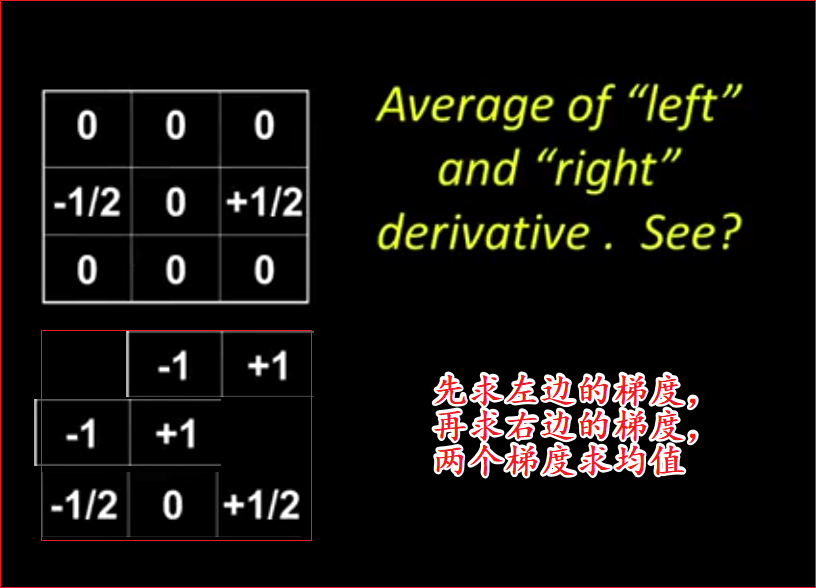
两个梯度求均值相关核会出现
1
2
frac{1}{2}
21
13.Sobel Operator

人们研究求图像梯度已经好多年了,最常用的就是使用
s
o
b
e
l
sobel
sobel算子
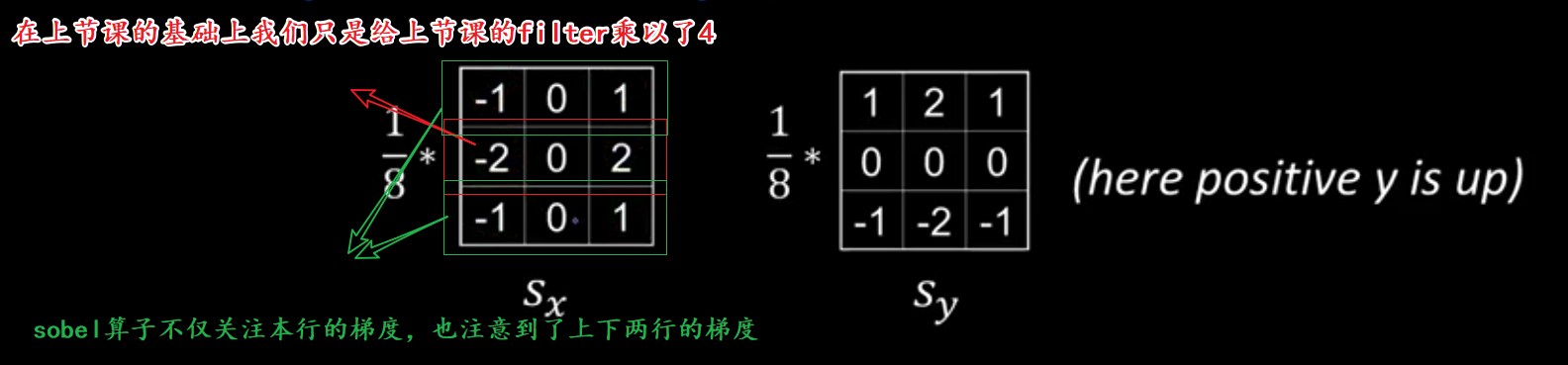
你可能会好奇,为啥前面要除以一个8呢??
想想上节课
∣
−
1
2
∣
0
∣
+
1
2
∣
|-frac{1}{2}| 0 |+frac{1}{2}|
∣−21∣ 0 ∣+21∣是正常的求一个梯度
那
∣
−
2
∣
0
∣
+
2
∣
|-2| 0 |+2|
∣−2∣ 0 ∣+2∣就是在该基础上乘以4,
∣
−
1
∣
0
∣
+
1
∣
|-1| 0 |+1|
∣−1∣ 0 ∣+1∣就是在该基础上乘以2
所以相当于求了8次
∣
−
1
2
∣
0
∣
+
1
2
∣
|-frac{1}{2}| 0 |+frac{1}{2}|
∣−21∣ 0 ∣+21∣
为了归一化 ( n o r m a l i z a t i o n ) (normalization) (normalization)所以要除以8
这里再说明一下,在matlab的imgradientxy函数中,求梯度默认亦是使用sobel算子,但是并不会除以8(可能是为了计算速度?)
另外需注意,在sobel算子中, S y S_{y} Sy的正方向为向上

上图是应用sobel算子求梯度,然后再求幅值所得图像,再取阈值之后得到右边的图片
可以说这张边界图片不是太好,也不是太坏!
14. Well Known Gradients
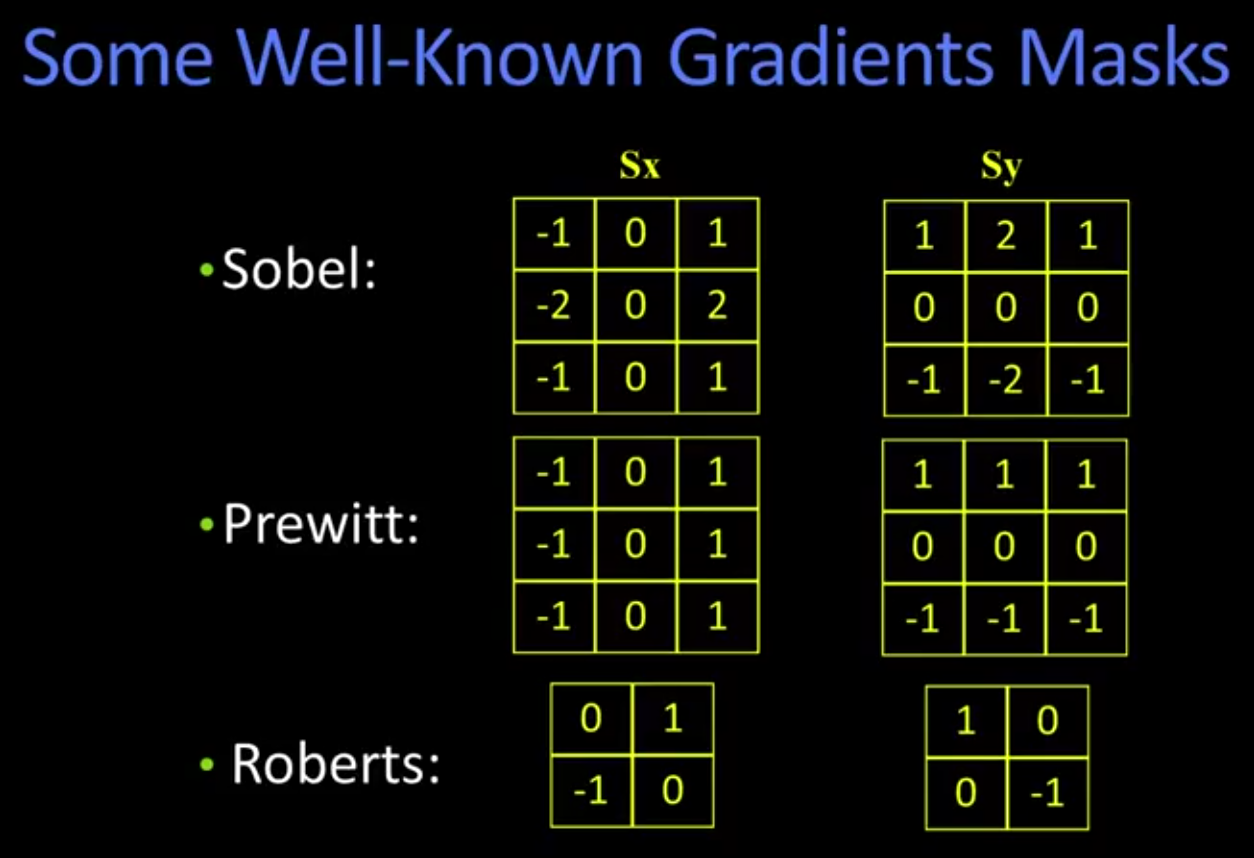
这里还有其他有名的求梯度的算子,老铁们瞅一瞅
15. Compute Gradients Quiz

这是我不用开字母的一节,因为教授是照着题目念的
16. Compute Gradients Quiz Solution

根据之前的操作,我们当然知道是相关操作,但是如果我们知道了怎么操作,卷积还是相关他就不影响了。
教授原话:
Look, as long as you keep track of what’s going on, it doesn’t matter.
17. Gradient Direction Quiz

给定上左图,对其使用连个方向的索贝尔算子,得到右边梯度两图
计算梯度的幅值和方向,得到下图:
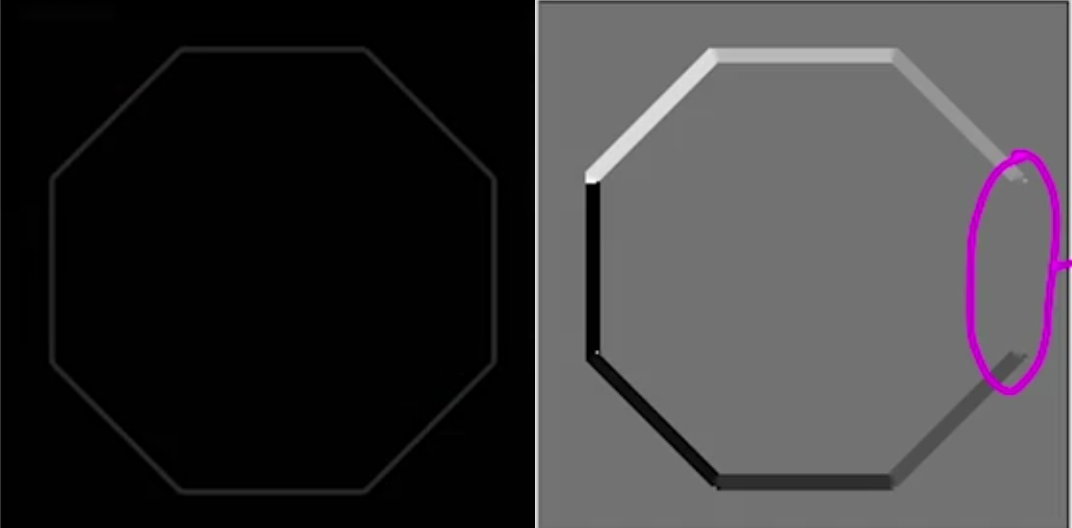
通过幅值显示的边界很清晰,下图是各边界的角度:
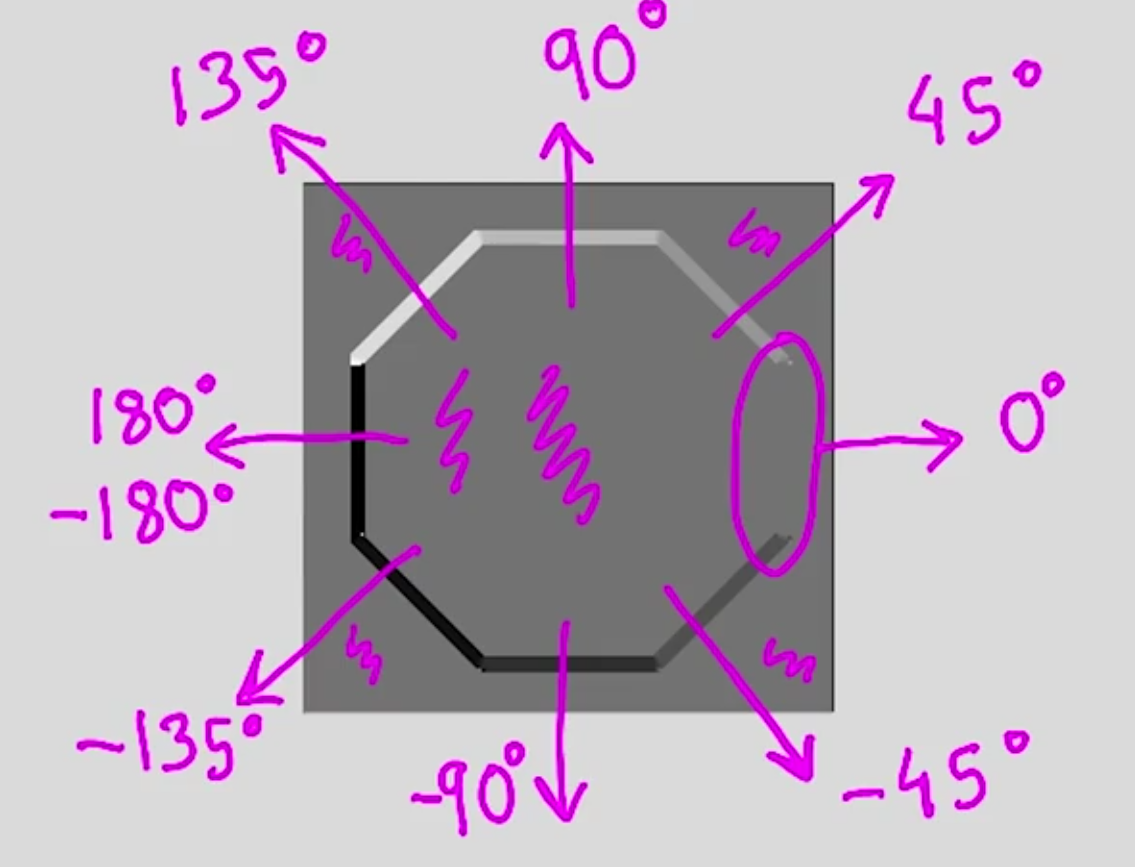
但是显示的方向图有些哪一理解:为什么,右边的边是0度呢?
回忆下之前的公式:

它是,
y
y
y方向的变化量除以
x
x
x方向的变化量的比值,再求其反正切值,而最右边的那条边,
y
y
y方向的变化量显然为零,
x
x
x方向的变化量显然是某一常数,所以其比值为0
你可能又要问了,为何最下面的边是-90度,我不是+90度呢? 回想上边的原图,$x$方向的变化量显然为0,而$x$方向的变化量如何计算呢?
注意在sobel算子中, y y y正方向为向上,所以 y y y方向的变化量为某一负的常数
所以 ∂ f ∂ y / ∂ f ∂ x frac{partial f}{partial y} / frac{partial f}{partial x} ∂y∂f/∂x∂f为负无穷
在下图 a r c t a n ( x ) arctan(x) arctan(x)中, − ∞ -infty −∞时的取值为-90度
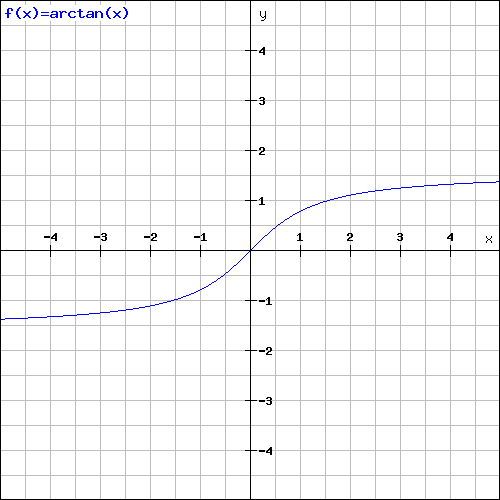
那么问题来了,我们如何提取特定角度的边呢?
18. Gradient Direction Quiz Solution
只需给梯度方向角度设定阈值,提取对应的边的mask,再对边界图片做掩膜操作即可
19. But in the Real World
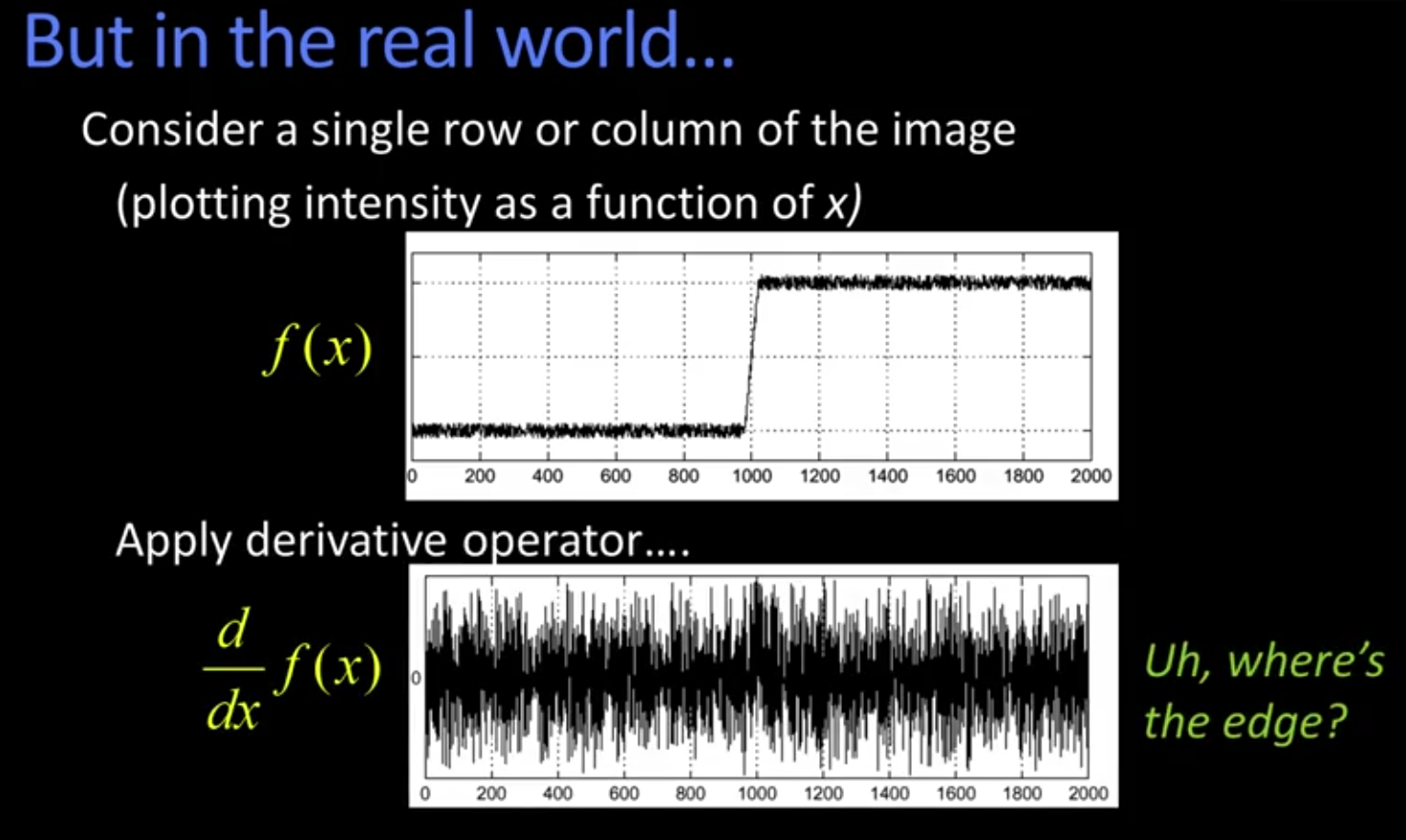
但是在实际图片中,会有许多噪声,我们对图片求导,会得到一个很尴尬的结果,导致我们无法准确找到边界的位置
这是给之前的结果添加高斯噪声的结果,画面越来越粗糙
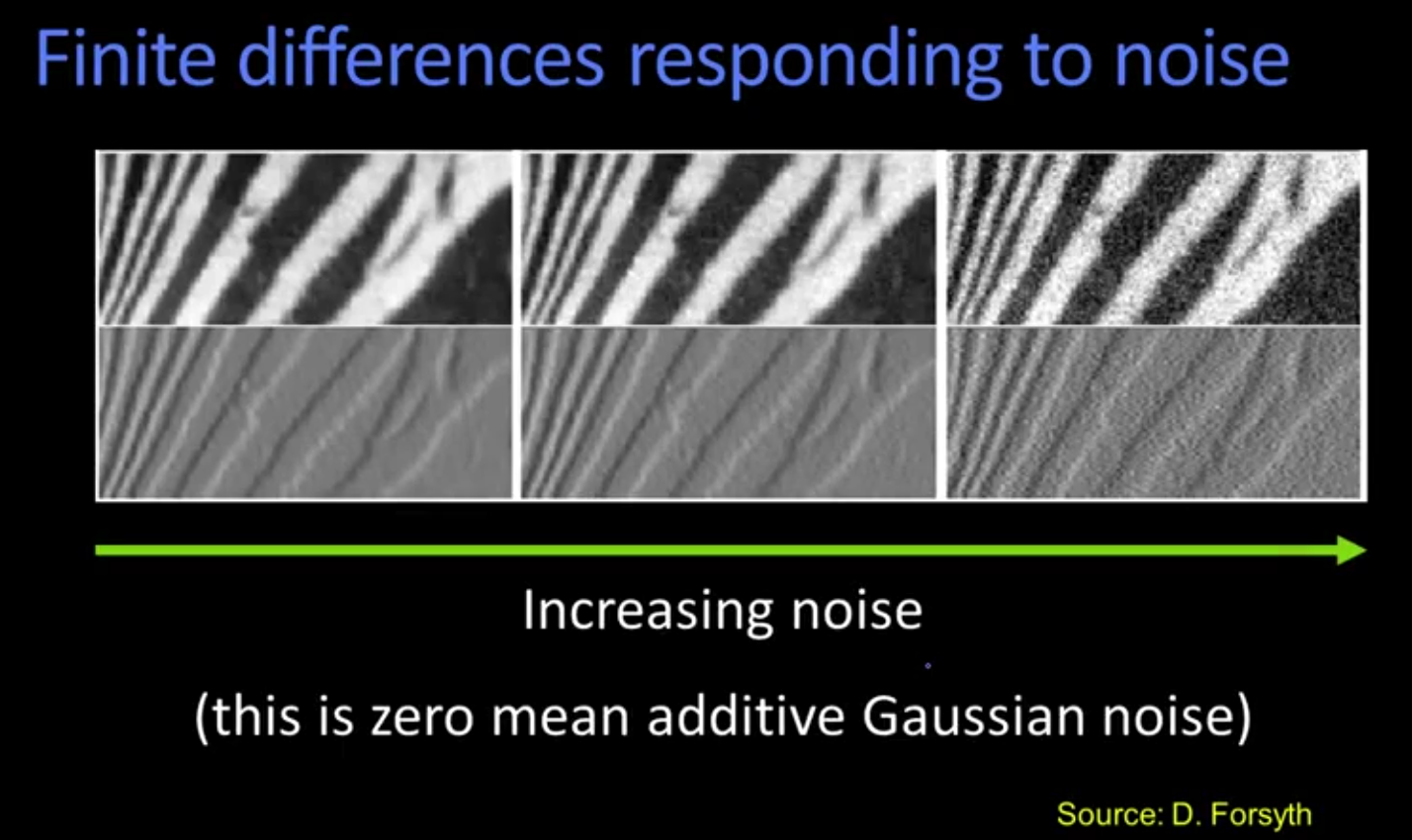
这时我们就应该给图片做平滑操作,给图片做高斯滤波即可
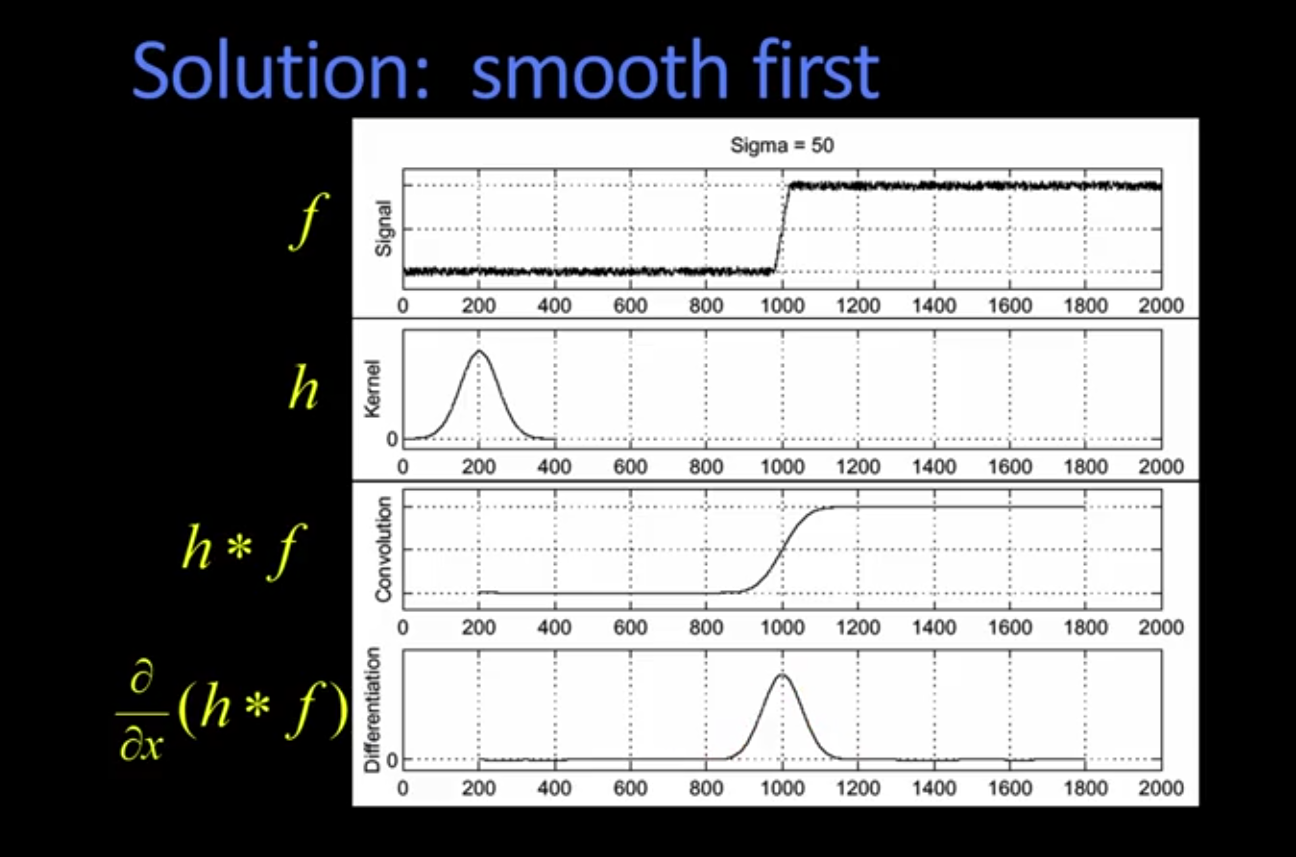
但是给图片做完高斯滤波再去求导,计算量太大,根据卷积或着相关的性质:
我们可以先对卷积核求导,然后以得到的结果对图片做滤波即可
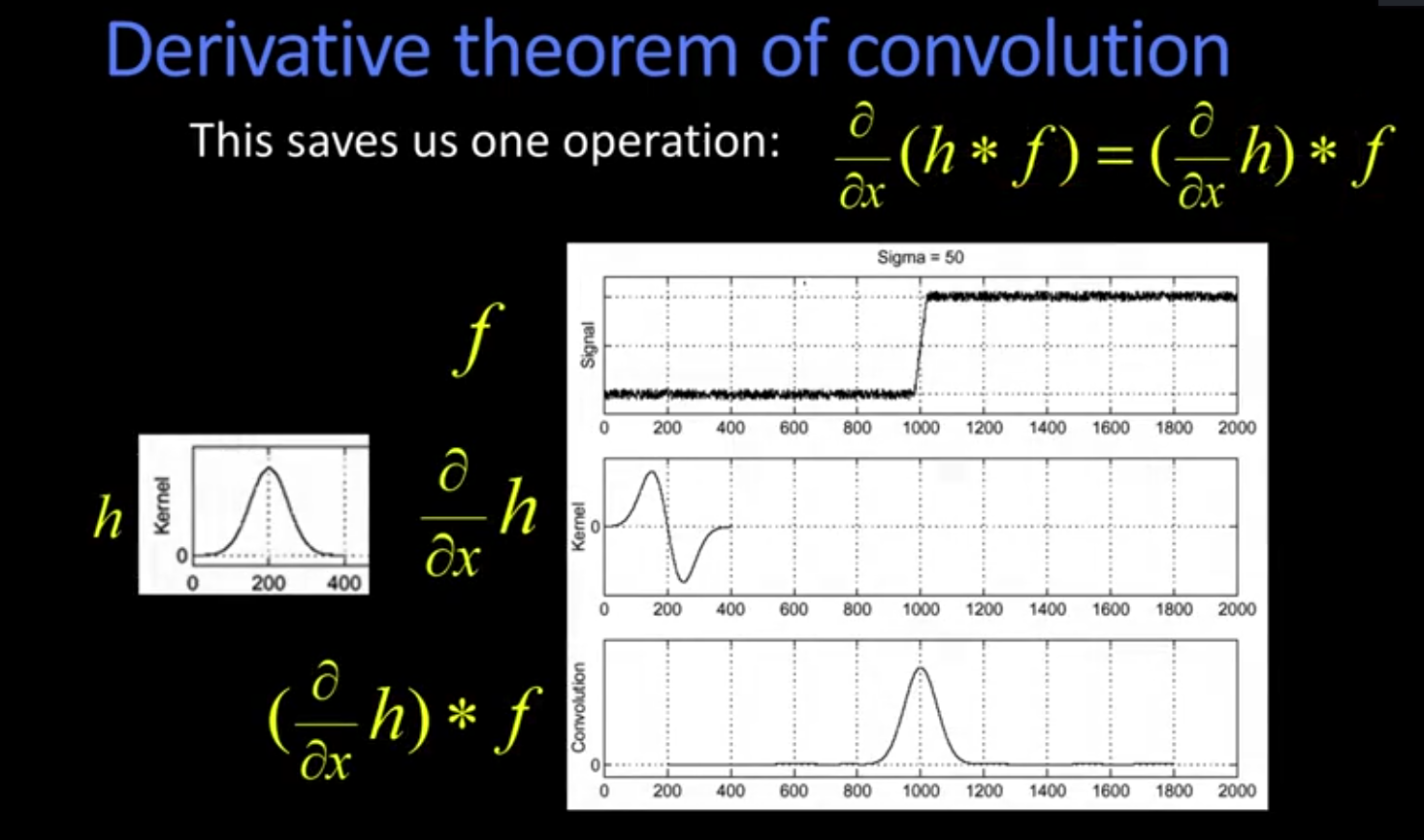
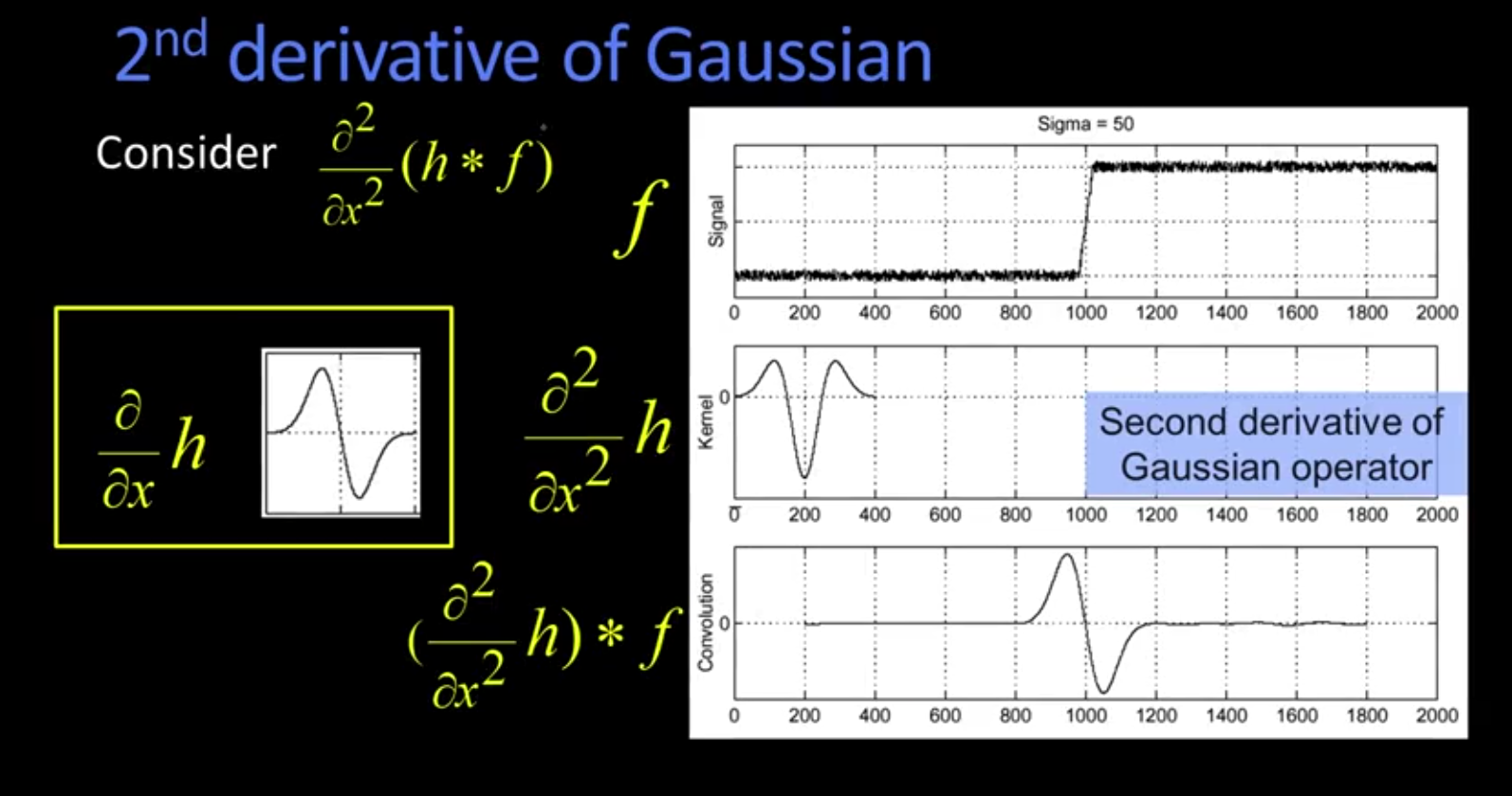
我们只需找到这次卷积操作之后的峰值即可,峰值即是边界,但是实际操作中,峰值在离散空间不太好找,所以,我们对高斯滤波器求二阶导数,再对图片滤波,找到结果为0的点即可
20. Linearity Property Quiz
以下哪一个线性性质,使得我们的计算量减少:

21. Linearity Property Quiz Solution
以下答案为D
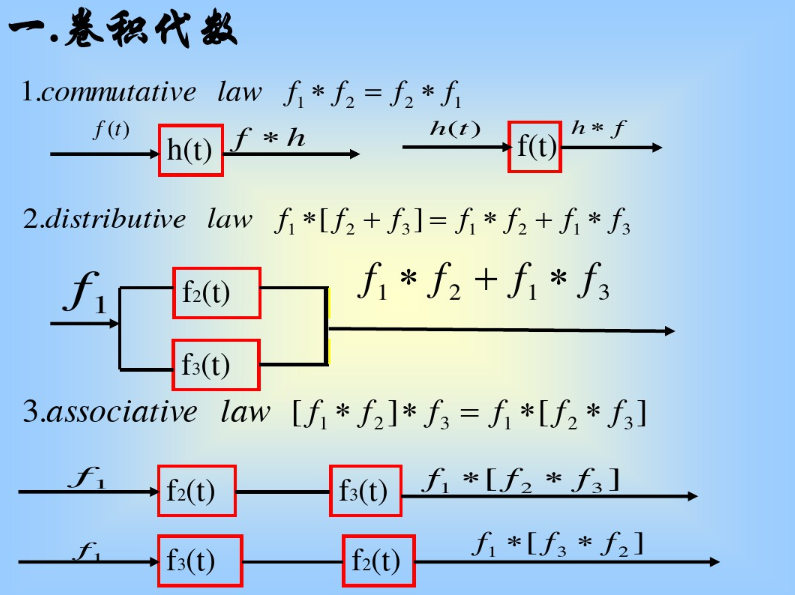
以下摘自百度文库:
https://wenku.baidu.com/view/df570e146edb6f1aff001f6e.html

22. The end

在一维方向上求梯度结束,下一节让我们看看在2维方向上求梯度
最后
以上就是美好电话最近收集整理的关于Georgia Tech计算视觉学习笔记:Edge detection: Gradients的全部内容,更多相关Georgia内容请搜索靠谱客的其他文章。








发表评论 取消回复